Ejercicio: 1Eva_2024PAOI_T1 Vaciado de reservorio semiesférico
literal a. Planteamiento
A partir de la solución expresión propuesta y simplificada del ejercicio, se reemplaza los valores de R, K, a y g que son constantes. Como se da el valor de t=(15 min)(60 s/min), se unifica la unidad de medida de tiempo a segundos pues g=9.6 m/s2.
-\frac{4}{3}R h^{3/2} + \frac{2}{5} h^{5/2} = -\frac{Ka}{\pi} t \sqrt{2g}
-\frac{4}{3}(3) h^{3/2} + \frac{2}{5} h^{5/2} = -\frac{(0.85)(0.01)}{\pi} (15)(60) \sqrt{2(9.8)}
la función para encontrar la raíz se reordena como f(h)=0
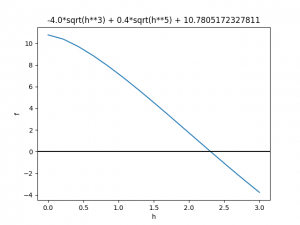
f(h) = -\frac{4}{3}(3) h^{3/2} + \frac{2}{5} h^{5/2} +\frac{(0.85)(0.01)}{\pi} (15)(60) \sqrt{2(9.8)} f(h) = -4h^{3/2} + 0.4 h^{5/2} +10.7805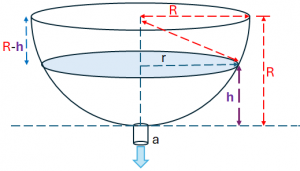
Usando la gráfica proporcionada del reservorio semiesférico, el valor de h no puede superar la altura R. Al vaciar el reservorio h=0.
Por lo que el intervalo a usar es [0,3]. Se verifica la existencia de una raíz al con la gráfica y Python.
b. Método de Newton Raphson
El método requiere la derivada f'(h)
f(h) = -4h^{3/2} + 0.4 h^{5/2} +10.7805 f'(h) = -6\frac{ h^{3/2}}{h} + \frac{h^{5/2}}{h} f'(h) = -6 h^{1/2}+ h^{3/2}El valor inicial puede ser por ejemplo, el centro del intervalo:
x_0= \frac{a+b}{2} = \frac{0+3}{2} = 1.5itera=0
f(1.5) = -4(1.5)^{3/2} + 0.4 (1.5)^{5/2} +10.7805= 4.5343 f'(1.5) = -6\frac{ 1.5^{3/2}}{1.5} + \frac{1.5^{5/2}}{1.5} = -5.5113 x_1= x_0 - \frac{f(1.5)}{f'(1.5)}= 1.5-\frac{4.5343}{-5.5113} =2.3227 error_1 =|x1-x0| = |2.3227-1.5| =0.8227itera=1
f(2.3227) = -4(2.3227)^{3/2} + 0.4 (2.3227)^{5/2} +10.7805= -0.09019 f'(2.3227) = -6\frac{ 2.3227^{3/2}}{2.3227} + \frac{2.3227^{5/2}}{2.3227} = -5.6043 x_2= 2.3227-\frac{-0.09019}{-5.6043} = 2.3066 error_2 = |2.3066-2.3227| =0.01611itera=2
f(2.3227) = -4(2.3066)^{3/2} + 0.4 (2.3066)^{5/2} +10.7805= -0.0007104 f'(2.3227) = -6\frac{ 2.3227^{3/2}}{2.3227} + \frac{2.3227^{5/2}}{2.3227} = -5.6093 x_3= 2.3227-\frac{-0.0007104}{-5.6093} = 2.3066 error_3 = |2.3066-2.3066| =0.000007241literal c, convergencia
considerando tolerancia de 10-3 (milimétrica), solo serán necesarias 3 iteraciones.
El método converge al mostrarse que los errores disminuyen en cada iteración.
El resultado se encuentra dentro del intervalo y es x = 2.3066
Algoritmo con Python
resultados:
fh:
____ ____
/ 3 / 5
- 4.0*\/ h + 0.4*\/ h + 10.7805172327811
dfh:
____ ____
/ 3 / 5
6.0*\/ h 1.0*\/ h
- ----------- + -----------
h h
['xi', 'xnuevo', 'tramo']
[[1.5000e+00 2.3227e+00 8.2272e-01]
[2.3227e+00 2.3066e+00 1.6118e-02]
[2.3066e+00 2.3066e+00 7.2412e-06]]
raiz en: 2.306612665792577
con error de: 7.241218404896443e-06
>>> f(1.5)
4.534318388683996
>>> df(1.5)
-5.5113519212621505
>>> f(2.3227)
-0.09019959114247378
>>> df(2.3227)
-5.604354799446854
>>> f(2.3066)
7.104683901282272e-05
>>> df(2.3066)
-5.609349350102558
instrucciones:
# 1Eva_2024PAOI_T1 Vaciado de reservorio semiesférico import numpy as np import matplotlib.pyplot as plt import sympy as sym # INGRESO h = sym.Symbol('h') t = 15*60 R = 3 g = 9.8 area = 0.01 K = 0.85 fh = -(4/3)*R*sym.sqrt(h**3)+(2/5)*sym.sqrt(h**5)+(K*area/np.pi)*np.sqrt(2*g)*(t) # Grafica de f(h) a = 0 b = 3 muestras = 15 # PROCEDIMIENTO hi = np.linspace(a,b,muestras) # para evaluación numérica con numpy f = sym.lambdify(h,fh) fi = f(hi) # derivada con sympy dfh = sym.diff(fh,h,1) df = sym.lambdify(h,dfh) # SALIDA print('fh:') sym.pprint(fh) print('dfh:') sym.pprint(dfh) plt.plot(hi,fi) plt.axhline(0, color='black') plt.xlabel('h') plt.ylabel('f') plt.title(fh) plt.show() ## Método de Newton-Raphson # INGRESO fx = f dfx = df x0 = (a+b)/2 # mitad del intervalo (ejemplo) tolera = 0.001 # PROCEDIMIENTO tabla = [] tramo = abs(2*tolera) xi = x0 while (tramo>=tolera): xnuevo = xi - fx(xi)/dfx(xi) tramo = abs(xnuevo-xi) tabla.append([xi,xnuevo,tramo]) xi = xnuevo # convierte la lista a un arreglo. tabla = np.array(tabla) n = len(tabla) # SALIDA print(['xi', 'xnuevo', 'tramo']) np.set_printoptions(precision = 4) print(tabla) print('raiz en: ', xi) print('con error de: ',tramo)