Ejercicio: 1Eva_IT2010_T2_MN Uso de televisores
Para la función dada:
p(x) =\frac{1}{2.5} \Big(-10 \sin \Big(\frac{12x}{7} \Big) e^{-\frac{24x}{7}} + \frac{48x}{7}e^{-\frac{8x}{7}} + 0.8 \Big)0≤x≤4
literal a
El enunciado indica encontrar el máximo y luego el mínimo, por lo que la curva bajo análisis es la derivada de la función dp(x)/dx. 
Adicionalmente, para encontrar los puntos se requiere usar el método de Newton-Raphson que corresponden a las raíces de dp(x)/dx. La función bajo análisis ahora es la derivada y para el método se usa la derivada: d2p(x)/dx2.
Al usar el computador para las fórmulas, se usa la forma simbólica de la función p(x), para obtener dpx y d2px.
primera derivada: -3.13469387755102*x*exp(-8*x/7) + 2.74285714285714*exp(-8*x/7) + 13.7142857142857*exp(-24*x/7)*sin(12*x/7) - 6.85714285714286*exp(-24*x/7)*cos(12*x/7) segunda derivada: 3.58250728862974*x*exp(-8*x/7) - 6.26938775510204*exp(-8*x/7) - 35.265306122449*exp(-24*x/7)*sin(12*x/7) + 47.0204081632653*exp(-24*x/7)*cos(12*x/7)
La gráfica requiere la evaluación las funciones, que por simplicidad de evaluación, su formas simbólicas se convierten a su forma 'lambda'.
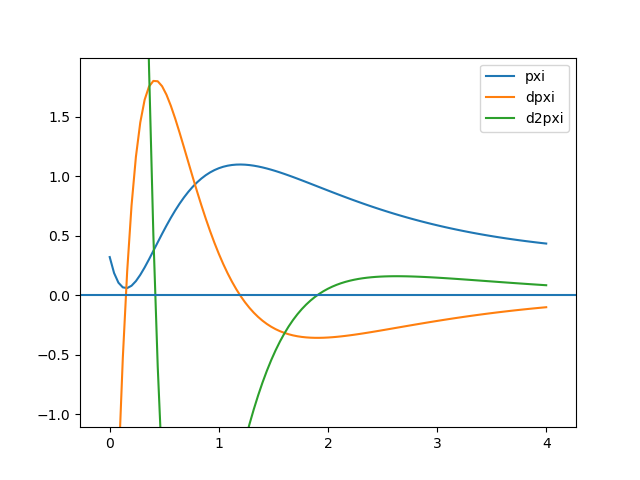
Con la gráfica se verifica que la raíz de dp(x)/dx (en naranja) pasa por el máximo y mínimo de p(x) (en azul).
que se obtienen con las siguientes instrucciones en Python:
# 1ra Evaluación I Término 2010 # tema 2. encendido tv # Tarea: aplicar el método de Newton-Raphson # solo se muestra la función y sus derivadas 1 y 2 import numpy as np import sympy as sym import matplotlib.pyplot as plt # función bajo análisis en forma simbólica x = sym.Symbol('x') pxs = (1/2.5)*(-10*sym.sin(12*x/7)*sym.exp(-24*x/7) \ + (48*x/7)*sym.exp(-8*x/7)+0.8) # derivadas dpxs = pxs.diff(x,1) d2pxs = pxs.diff(x,2) d2pxs = sym.expand(d2pxs) # SALIDA print('primera derivada: ') print(dpxs) print('segunda derivada: ') print(d2pxs) # conversion a lambda pxn = sym.utilities.lambdify(x,pxs, 'numpy') dpxn = sym.utilities.lambdify(x,dpxs, 'numpy') d2pxn = sym.utilities.lambdify(x,d2pxs, 'numpy') # observar gráfica a = 0 b = 4 muestras = 51 tolera = 0.0001 xi = np.linspace(a,b, muestras) pxi = pxn(xi) dpxi = dpxn(xi) d2pxi = d2pxn(xi) # Gráfica plt.plot(xi,pxi, label = 'pxi') plt.plot(xi,dpxi, label = 'dpxi') plt.plot(xi,d2pxi, label = 'd2pxi') plt.axhline(0) plt.legend() plt.show()
literal b
Usando el método de Newton-Raphson a partir de la primera y segunda derivada según lo planteado, usando x0=0,se tiene:
f(x) = -3.13469387755102 x e^{(-8 x/7)} +2.74285714285714 e^{(-8 x/7)} + 13.7142857142857 e^{(-24 x/7)} \sin\Big(\frac{12x}{7}\Big) - 6.85714285714286 e^{(-24x/7)} \cos\Big(\frac{12x}{7}\Big) f'(x) = 3.58250728862974 x e^{(- 8 x/7)} - 6.26938775510204 e^{(- 8 x/7)} - 35.265306122449 e^{(-24x/7)} \sin \Big(\frac{12x}{7}\Big) + 47.0204081632653 e^{(-24x/7)} \cos\Big(\frac{12x}{7}\Big)itera = 0, x0 = 0
f(0) = -3.13469387755102 (0) e^{(-8 (0)/7)} +2.74285714285714 e^{(-8 (0)/7)} + 13.7142857142857 e^{(-24 (0)/7)} \sin\Big(\frac{12(0)}{7}\Big) - 6.85714285714286 e^{(-24(0)/7)} \cos\Big(\frac{12(0)}{7}\Big) = -4.1143 f'(0) = 3.58250728862974 (0) e^{(- 8 (0)/7)} - 6.26938775510204 e^{(- 8(0)/7)} - 35.265306122449 e^{(-24(0)/7)} \sin \Big(\frac{12(0)}{7}\Big) + 47.0204081632653 e^{(-24(0)/7)} \cos\Big(\frac{12(0)}{7}\Big) = 40.751 x_1 = 0 - \frac{-4.1143}{40.751} =0.101 error = | 0.101-0 |=0.101itera = 1
f(0.101) = -3.13469387755102 (0.101) e^{(-8 (0.101)/7)} +2.74285714285714 e^{(-8 (0.101)/7)} + 13.7142857142857 e^{(-24 (0.101)/7)} \sin\Big(\frac{12(0.101)}{7}\Big) - 6.85714285714286 e^{(-24(0.101)/7)} \cos\Big(\frac{12(0.101)}{7}\Big) = -0.9456 f'(0.101) = 3.58250728862974 (0.101) e^{(- 8 (0.101)/7)} - 6.26938775510204 e^{(- 8 (0.101)/7)} - 35.265306122449 e^{(-24(0.101)/7)} \sin \Big(\frac{12(0.101)}{7}\Big) + 47.0204081632653 e^{(-24(0.101)/7)} \cos\Big(\frac{12(0.101)}{7}\Big) =23.2054 x_2 = 0.101 - \frac{-0.9456}{23.2054} =0.1417 error = | 0.1417-0.101 |=0.0407itera = 2
f(0.1417) = -3.13469387755102 (0.1417) e^{(-8 (0.1417)/7)} +2.74285714285714 e^{(-8 (0.1417)/7)} + 13.7142857142857 e^{(-24 (0.1417)/7)} \sin\Big(\frac{12(0.1417)}{7}\Big) - 6.85714285714286 e^{(-24(0.1417)/7)} \cos\Big(\frac{12(0.1417)}{7}\Big) = -0.11005 f'(0.1417) = 3.58250728862974 (0.1417) e^{(- 8 (0.1417)/7)} - 6.26938775510204 e^{(- 8 (0.1417)/7)} - 35.265306122449 e^{(-24(0.1417)/7)} \sin \Big(\frac{12(0.1417)}{7}\Big) + 47.0204081632653 e^{(-24(0.1417)/7)} \cos\Big(\frac{12(0.1417)}{7}\Big) = 0.17957 x_3 = 0.1417 - \frac{-0.11005}{0.17957} =0.14784 error = | 0.14784- 0.1417 |=0.0061287se observa que el error disminuye en cada iteración, por lo que el método converge.
Se continúan las operaciones con el algoritmo obteniendo:
i ['xi', 'fi', 'dfi', 'xnuevo', 'tramo'] 0 [ 0. -4.1143 40.751 0.101 0.101 ] 1 [ 0.101 -0.9456 23.2054 0.1417 0.0407] 2 [ 1.4171e-01 -1.1005e-01 1.7957e+01 1.4784e-01 6.1287e-03] 3 [ 1.4784e-01 -2.1916e-03 1.7245e+01 1.4797e-01 1.2708e-04] 4 [ 1.4797e-01 -9.2531e-07 1.7231e+01 1.4797e-01 5.3701e-08] raíz en: 0.1479664890264113
literal c
la otra raíz se encuentra con x0=1
i ['xi', 'fi', 'dfi', 'xnuevo', 'tramo'] 0 [ 1. 0.3471 -2.207 1.1573 0.1573] 1 [ 1.1573 0.0539 -1.5338 1.1924 0.0352] 2 [ 1.1924 0.0024 -1.397 1.1941 0.0017] 3 [ 1.1941e+00 5.7065e-06 -1.3904e+00 1.1942e+00 4.1041e-06] raíz en: 1.1941511721360376
Instrucciones en Python
# 1Eva_IT2010_T2_MN Uso de televisores import numpy as np import matplotlib.pyplot as plt def newton_raphson(fx,dfx,xi, tolera, iteramax=100, vertabla=False, precision=4): ''' funciónx y fxderiva en forma numérica lambda xi es el punto inicial de búsqueda ''' itera=0 tramo = abs(2*tolera) if vertabla==True: print('i', ['xi','fi','dfi', 'xnuevo', 'tramo']) np.set_printoptions(precision) while (tramo>=tolera and itera<iteramax): fi = fx(xi) dfi = dfx(xi) xnuevo = xi - fi/dfi tramo = abs(xnuevo-xi) if vertabla==True: print(itera,np.array([xi,fi,dfi,xnuevo,tramo])) xi = xnuevo itera = itera + 1 if itera>=iteramax: xi = np.nan print('itera: ',itera, 'No converge,se alcanzó el máximo de iteraciones') return(xi) # INGRESO fx = lambda x: -3.13469387755102*x*np.exp(-8*x/7) \ + 2.74285714285714*np.exp(-8*x/7) \ + 13.7142857142857*np.exp(-24*x/7)*np.sin(12*x/7) \ - 6.85714285714286*np.exp(-24*x/7)*np.cos(12*x/7) dfx = lambda x: (3.58250728862974*x - 6.26938775510204 \ - 35.265306122449*np.exp(-16*x/7)*np.sin(12*x/7) \ + 47.0204081632653*np.exp(-16*x/7)*np.cos(12*x/7))*np.exp(-8*x/7) x0 = 0.5 tolera = 0.0001 # PROCEDIMIENTO respuesta = newton_raphson(fx,dfx,x0, tolera, vertabla=True) # SALIDA print('raíz en: ', respuesta)