s1Eva_IT2011_T1 Encontrar α en integral

Ejercicio: 1Eva_IT2011_T1 Encontrar α en integral

Desarrollo Analítico

Se iguala la ecuación al valor buscado = 10, y se resuelve

\int_{\alpha}^{2\alpha} x e^{x}dx = 10

siendo: μ = x , δv = e^x, δu = δx , v = e^x

\int u dv = uv - \int v \delta u xe^x \Big|_{\alpha}^{2 \alpha} - \int_{\alpha}^{2\alpha} e^{x}dx - 10 = 0 2\alpha e^{2 \alpha} -\alpha e^{\alpha} - (e^{2\alpha} - e^{\alpha}) - 10 = 0 (2\alpha-1)e^{2 \alpha}+ (1-\alpha) e^{\alpha} - 10 = 0

la función a usar en el método es

f(\alpha) = (2\alpha-1)e^{2 \alpha}+ (1-\alpha)e^{\alpha} -10

Se obtiene la derivada para el método de Newton Raphson

f'(\alpha) = 2e^{2 \alpha} + 2(2\alpha-1)e^{2 \alpha} - e^{\alpha} + (1-\alpha) e^{\alpha} f'(\alpha) = (2 + 2(2\alpha-1))e^{2 \alpha} +(-1 + (1-\alpha)) e^{\alpha} f'(\alpha) = 4\alpha e^{2 \alpha} -\alpha e^{\alpha}

la fórmula para el método de Newton-Raphson

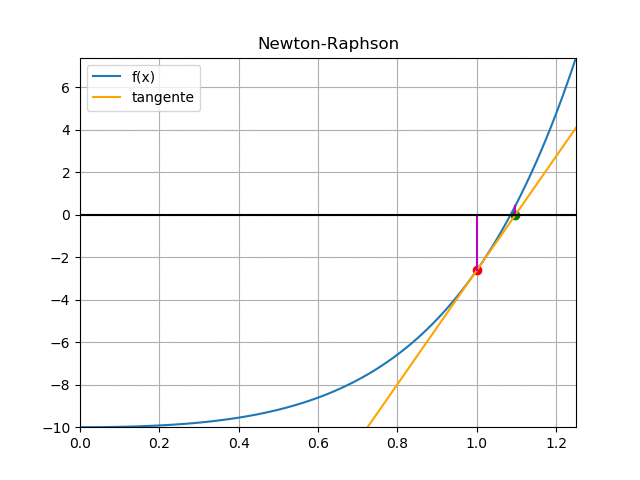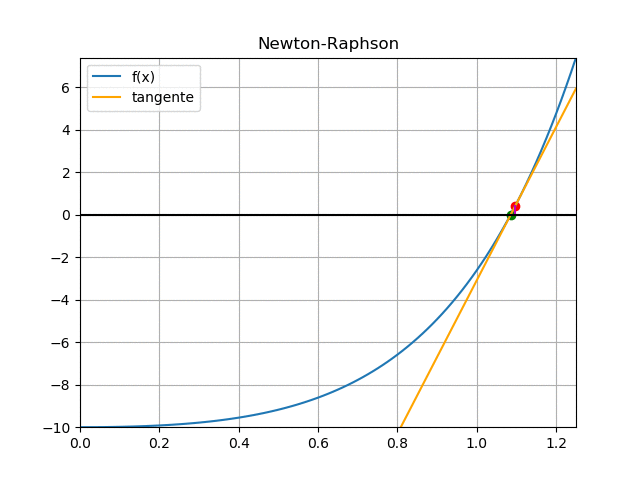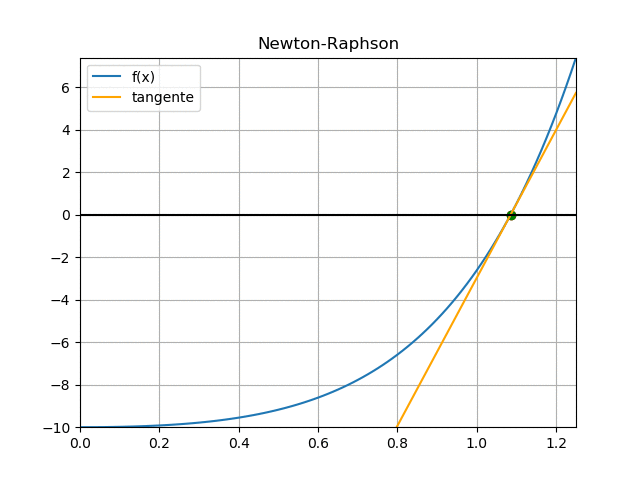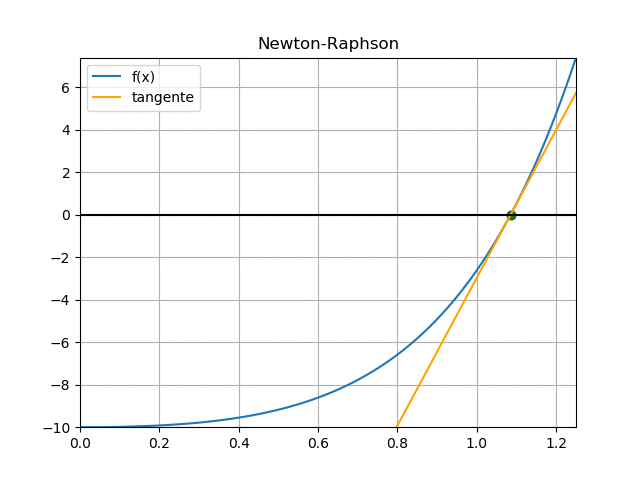
\alpha_{i+1} = \alpha_i - \frac{f(\alpha)}{f'(\alpha)}

se prueba con α₀ = 1, se evita el valor de cero por la indeterminación que se da por f'(0) = 0

iteración 1:

f(1) = (2(1)-1)e^{2(1)}+ (1-(1))e^{(1)} -10 f'(1) = 4(1) e^{2 (1)} -(1) e^{(1)} \alpha_{1} = 1- \frac{f(1)}{f'(1)}

\alpha_{1} = 1.0973
error = 0.0973

iteración 2:
f(2) = (2(1.0973)-1)e^{2(1.0973)}+ (1-(1.0973))e^{(1.0973)} -10

f'(2) = 4(1.0973) e^{2 (1.0973)} -(1.0973) e^{(1.0973)} \alpha_{2} = 1.0973 - \frac{f(1.0973)}{f'(1.0973)}

\alpha_{2} = 1.0853
error = 0.011941

iteración 3:
f(3) = (2(1.0853)-1)e^{2(1.0853)}+ (1-(1.0853))e^{(1.0853)} -10

f'(3) = 4(1.0853) e^{2 (1.0853)} -(1.0853) e^{(1.0853)} \alpha_{3} = 1.0853- \frac{f(1.0853)}{f'(1.0853)}

\alpha_{3} = 1.0851
error = 0.00021951

[  xi,          xnuevo,      f(xi),      f'(xi),       tramo ]
[  1.           1.0973      -2.6109      26.8379       0.0973]
[  1.0973e+00   1.0853e+00   4.3118e-01   3.6110e+01   1.1941e-02]
[  1.0853e+00   1.0851e+00   7.6468e-03   3.4836e+01   2.1951e-04]
[  1.0851e+00   1.0851e+00   2.5287e-06   3.4813e+01   7.2637e-08]
raiz:  1.08512526549

se obtiene el valor de la raíz con 4 iteraciones, con error de aproximación de 7.2637e-08

Desarrollo con Python