s1Eva_IT2018_T3 Temperatura en nodos de placa

Ejercicio: 1Eva_IT2018_T3 Temperatura en nodos de placa

a) Plantear el sistema de ecuaciones. Usando el promedio para cada nodo interior: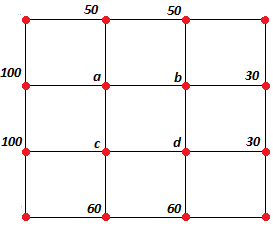

$a=\frac{50+c+100+b}{4}$ $b=\frac{a+30+50+d}{4}$ $c=\frac{a+60+100+d}{4}$ $d=\frac{b+60+c+30}{4}$

que reordenando se convierte en:

$4a=150+c+b$ $4b=a+80+d$ $4c=a+160+d$ $4d=b+c+90$

simplificando:

$4a-b-c= 150$ $a-4b+d = -80$ $a-4c+d = -160$ $b+c-4d = -90$

que a forma matricial se convierte en:

A = [[ 4, -1, -1, 0.0],
     [ 1, -4,  0, 1.0],
     [ 1,  0, -4, 1.0],
     [ 0,  1,  1,-4.0]]
B = [[ 150.0],
     [ -80.0],
     [-160.0],
     [ -90.0]]

Observación: la matriz A ya es diagonal dominante, no requiere pivotear por filas.  Se aumentó el punto decimal a los valores de la matriz A y el vector B  para que sean considerados como números reales.

El número de condición es: np.linalg.cond(A) = 3.0

que es cercano a 1 en un orden de magnitud, por lo que la solución matricial es «estable» y los cambios en los coeficientes afectan proporcionalmente a los resultados. Se puede aplicar métodos iterativos sin mayores inconvenientes.

b y c) método de Jacobi para sistemas de ecuaciones, con vector inicial

 
X(0) = [[60.0],
        [40], 
        [70],
        [50]] 

reemplazando los valores iniciales en cada ecuación sin cambios.

iteración 1
$a=\frac{50+70+100+40}{4} = 65$

$b=\frac{60+30+50+50}{4} = 47.5$ $c=\frac{60+60+100+50}{4} = 67.5$ $d=\frac{40+60+70+30}{4} = 50$

X(1) = [[65],
        [47.5],
        [67.5],
        [50]]

vector de error = 
     [|65-60|,
      |47.5-40|,
      |67.5-70|,
      |50-50|]
  = [|5|,
     |7.5|,
     |-2.5|,
     |0|]
errormax = 7.5

iteración 2
$a=\frac{50+67.5+100+47.5}{4} = 66.25$

$b=\frac{65+30+50+50}{4} = 48.75$ $c=\frac{65+60+100+50}{4} = 68.75$ $d=\frac{47.5+60+67.7+30}{4} = 51.3$

X(2) = [[66.25],
        [48.75],
        [68.75],
        [51.3]]

vector de error = 
       [|66.25-65|,
        |48.75-47.5|,
        |68.75-67.5|,
           |51.3-50|] 
  = [|1.25|,
     |1.25|,
     |1.25|,
     |1.3|]
errormax = 1.3

iteración 3
$a=\frac{50+68.75+100+48.75}{4} = 66.875$

$b=\frac{66.25+30+50+51.3}{4} = 49.38$ $c=\frac{66.25+60+100+51.3}{4} = 69.3875$ $d=\frac{48.75+60+68.75+30}{4} = 51.875$

X(2) = [[66.875],
        [49.38],
        [69.3875],
        [51.875]]

vector de error = 
      [|66.875-66.25|,
       |49.38-48.75|,
       |69.3875-68.75|,
       |51.875-51.3|]
    = [|0.655|,
       |0,63|,
       |0.6375|,
        |0.575|]
errormax = 0.655
con error relativo de:
100*0.655/66.875 = 0.97%

siguiendo las iteraciones se debería llegar a:

>>> np.linalg.solve(A,B)
array([[ 67.5],
       [ 50. ],
       [ 70. ],
       [ 52.5]])