s1Eva_IT2019_T2 Catenaria cable – Métodos numéricos

Ejercicio: 1Eva_IT2019_T2 Catenaria cable

Las fórmulas con las que se requiere trabajar son:

y = \frac{T_A}{w} cosh \Big( \frac{w}{T_A}x \Big) + y_0 - \frac{T_A}{w}

Donde la altura y del cable está en función de la distancia x.

Además se tiene que:

cosh(z) = \frac{e^z+ e^{-z}}{2}

que sustituyendo la segunda en la primera se convierte en:

y = \frac{T_A}{w} \frac{e^{\frac{w}{T_A}x}+ e^{-\frac{w}{T_A}x}}{2} + y_0 - \frac{T_A}{w}

y usando los valores del enunciado w=12, y₀=6 , y=15, x=50 se convierte en:

15 = \frac{T_A}{12} \frac{e^{\frac{12}{T_A}50}+ e^{-\frac{12}{T_A}50}}{2} + 6 - \frac{T_A}{12}

simplificando, para usar el método de búsqueda de raíces:

\frac{1}{2}\frac{T_A}{12} e^{\frac{12}{T_A}50} + \frac{1}{2}\frac{T_A}{12} e^{-\frac{12}{T_A}50} - \frac{T_A}{12} - 9 = 0

cambiando la variable $\frac{12}{T_A}=x$

\frac{1}{2x} e^{50x} + \frac{1}{2x} e^{-50x} - \frac{1}{x}-9=0

la función a usar para la búsqueda de raíces es:

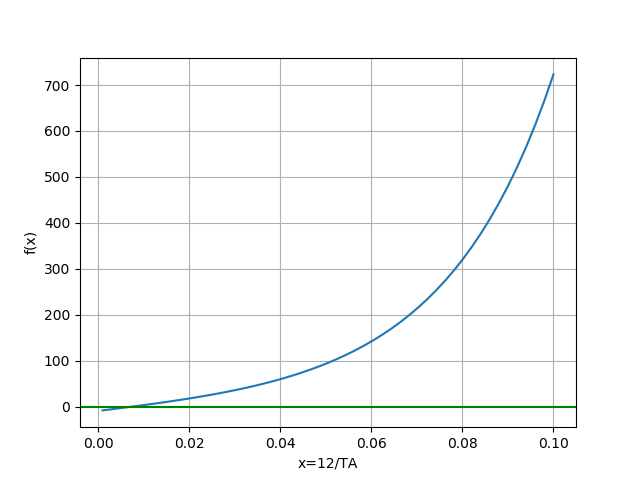
f(x)=\frac{1}{2x} e^{50x} + \frac{1}{2x} e^{-50x} - \frac{1}{x}-9

Para el método de Newton-Raphson se tiene que:

x_{i+1} = x_i -\frac{f(x_i)}{f'(x_i)}

por lo que se determina:

f'(x)= - \frac{1}{2x^2}e^{50x} + \frac{1}{2x}(50) e^{50x} +

- \frac{1}{2x^2} e^{-50x} + \frac{1}{2x}(-50)e^{-50x} + \frac{1}{x^2}

f'(x)= -\frac{1}{2x^2}[e^{50x}+e^{-50x}] +

+ \frac{25}{x}[e^{50x}-e^{-50x}] +\frac{1}{x^2}

f'(x)= \Big[\frac{25}{x} -\frac{1}{2x^2}\Big]\Big[e^{50x}+e^{-50x}\Big] +\frac{1}{x^2}

Con lo que se puede inicar las iteraciones.

Por no disponer de valor inicial para T_A, considere que el cable colgado no debería tener tensión T_A=0 N, pues en la forma x=12/T_A se crea una indeterminación. Si no dispone de algún criterio para seleccionar el valor de T_A puede iniciar un valor positivo, por ejemplo 120 con lo que el valor de x₀=12/120=0.1

Iteración 1

f(0.1)=\frac{1}{2(0.1)} e^{50(0.1)} + \frac{1}{2(0.1)} e^{-50(0.1)}

- \frac{1}{0.1}-9 =723.0994

f'(0.1)=\Big[\frac{25}{0.1} - \frac{1}{2(0.1)^2}\Big]\Big[e^{50(0.1)}+e^{-50(0.1)}\Big] +

+\frac{1}{(0.1)^2} = 29780.61043

x_{1} = 0.1 -\frac{723.0994}{29780.61043} = 0.07571

error = | x₁ – x₀| = | 0.07571 – 0.1| = 0.02428

Iteración 2

f(0.07571)=\frac{1}{2(0.07571)} e^{50(0.07571)}+

+ \frac{1}{2(0.07571)} e^{-50(0.07571)}

- \frac{1}{0.07571}-9 = 269.0042

f'(0.07571)= \Big[\frac{25}{0.07571} -\frac{1}{2(0.07571)^2}\Big].

.\Big[e^{50(0.07571)}+e^{-50(0.07571)}\Big] +

+\frac{1}{(0.07571)^2} = 10874.0462

x_{2} = 0.07571 -\frac{269.0042}{10874.0462} = 0.05098

error = | x₂ – x₁| = |0.05098- 0.02428| = 0.02473

Iteración 3

f(0.05098) = 97.6345

f'(0.05098) = 4144.1544

x_{3} = 0.0274

error = | x₃ – x₂| = |0.05098- 0.0274| = 0.0236

finalmente después de varias iteraciones, la raiz se encuentra en: 0.007124346154337298

que convitiendo

T_A = \frac{12}{x} = \frac{12}{0.0071243461}

= 1684.36 N

Revisión de resultados

Usando como base los algoritmos desarrollados en clase:

['xi', 'xnuevo', 'tramo']
[0.1    0.0757 0.0243]
[0.0757 0.051  0.0247]
[0.051  0.0274 0.0236]
[0.0274 0.0111 0.0163]
[0.0111 0.0072 0.0039]
[7.2176e-03 7.1244e-03 9.3199e-05]
[7.1244e-03 7.1243e-03 3.8351e-08]
raiz en:  0.007124346154337298
TA = 12/x =  1684.365096815854

Algoritmos Python usando el procedimiento de:

https://blog.espol.edu.ec/analisisnumerico/2-3-1-newton-raphson-ejemplo01/

# 1Eva_IT2019_T2 Catenaria cable
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
a = 0.001
b = 0.1
muestras = 51

x0 = 0.1
tolera = 0.00001

fx = lambda x: 0.5*(1/x)*np.exp(50*x) + 0.5*(1/x)*np.exp(-50*x)-1/x -9
dfx = lambda x: -0.5*(1/(x**2))*(np.exp(50*x)+np.exp(-50*x)) + (25/x)*(np.exp(50*x)-np.exp(-50*x)) + 1/(x**2)

# PROCEDIMIENTO
tabla = []
tramo = abs(2*tolera)
xi = x0
while (tramo>=tolera):
    xnuevo = xi - fx(xi)/dfx(xi)
    tramo = abs(xnuevo-xi)
    tabla.append([xi,xnuevo,tramo])
    xi = xnuevo

tabla = np.array(tabla)
n=len(tabla)

TA = 12/xnuevo

# para la gráfica
xp = np.linspace(a,b,muestras)
fp = fx(xp)

# SALIDA
print(['xi', 'xnuevo', 'tramo'])
np.set_printoptions(precision = 4)
for i in range(0,n,1):
    print(tabla[i])
print('raiz en: ', xi)
print('TA = 12/x = ', TA)

# Grafica
plt.plot(xp,fp)
plt.xlabel('x=12/TA')
plt.ylabel('f(x)')
plt.axhline(0, color = 'green')
plt.grid()
plt.show()