s2Eva_2022PAOII_T3 EDP Parabólica con coseno 3/4π

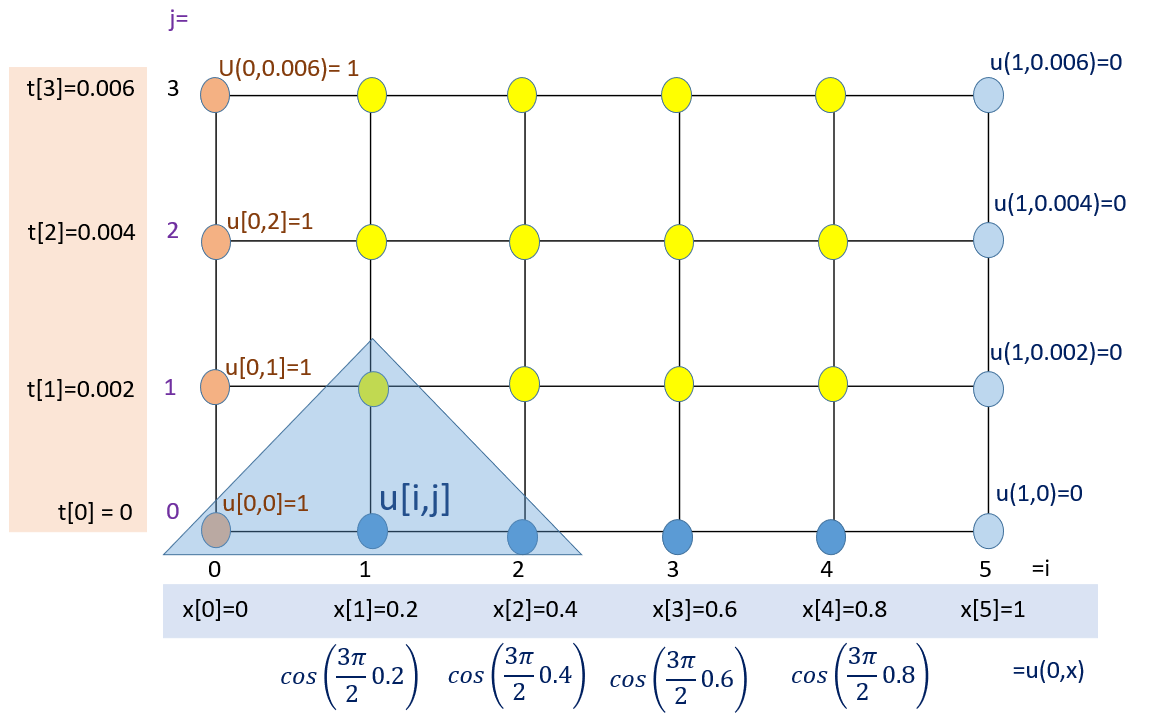
Ejercicio: 2Eva_2022PAOII_T3 EDP Parabólica con coseno 3/4π

\frac{\partial^2 u}{\partial x^2} = b \frac{\partial u}{\partial t}

\frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{(\Delta x)^2} = b\frac{u_{i,j+1}-u_{i,j}}{\Delta t}

agrupando variables

\frac{\Delta t}{b} \frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{(\Delta x)^2} = \frac{\Delta t}{b}b\frac{u_{i,j+1}-u_{i,j}}{\Delta t} λ = \frac{\Delta t}{b(\Delta x)^2} λ = \frac{0.002}{2(0.2)^2} =0.025

como λ<0.5 el método converge.

\lambda \Big[u[i+1,j]-2u[i,j]+u[i-1,j]\Big] = u[i,j+1]-u[i,j]

por el método explícito:

u[i,j+1] =\lambda \Big[u[i+1,j]-2u[i,j]+u[i-1,j]\Big] + u[i,j] u[i,j+1] =\lambda u[i+1,j]+(1-2\lambda)u[i,j]+\lambda u[i-1,j]

iteración i=1, j=0

u[1,1] =\lambda u[0,0]+(1-2\lambda)u[1,0]+\lambda u[2,0] u[1,1] =0.025(1) +(1-2(0.025))\cos \Big( \frac{3π}{2}0.2\Big)+0.025 \cos \Big( \frac{3π}{2}0.4\Big)

iteración i=2, j=0

u[2,1] =\lambda u[1,0]+(1-2\lambda)u[2,0]+\lambda u[3,0] u[2,1] =0.025\cos \Big( \frac{3π}{2}0.2\Big) +(1-2(0.025))\cos \Big( \frac{3π}{2}0.4\Big) +0.025 \cos \Big( \frac{3π}{2}0.6\Big)

iteración i=3, j=0

u[3,1] =\lambda u[2,0]+(1-2\lambda)u[3,0]+\lambda u[4,0] u[3,1] =0.025\cos \Big( \frac{3π}{2}0.4\Big) +(1-2(0.025))\cos \Big( \frac{3π}{2}0.6\Big) +0.025 \cos \Big( \frac{3π}{2}0.8\Big)

iteración i=4, j=0

u[4,1] =\lambda u[3,0]+(1-2\lambda)u[4,0]+\lambda u[5,0] u[4,1] =0.025\cos \Big( \frac{3π}{2}0.6\Big) +(1-2(0.025))\cos \Big( \frac{3π}{2}0.8\Big) +0.025 (0)

continuar con las iteraciones en el algoritmo

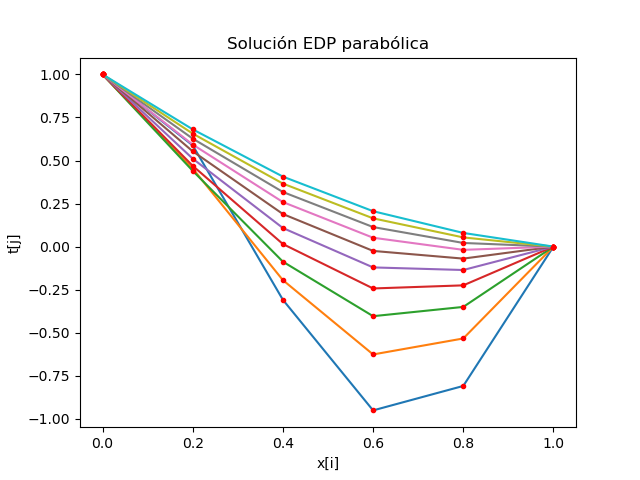
Resultados con el algoritmo

Tabla de resultados
[[ 1.    1.    1.    1.    1.    1.    1.    1.    1.    1.  ]
 [ 0.59  0.58  0.56  0.55  0.54  0.53  0.53  0.52  0.51  0.5 ]
 [-0.31 -0.3  -0.3  -0.29 -0.28 -0.28 -0.27 -0.27 -0.26 -0.26]
 [-0.95 -0.93 -0.91 -0.89 -0.88 -0.86 -0.84 -0.82 -0.81 -0.79]
 [-0.81 -0.79 -0.78 -0.76 -0.74 -0.73 -0.71 -0.7  -0.68 -0.67]
 [ 0.    0.    0.    0.    0.    0.    0.    0.    0.    0.  ]]

Instrucciones en Python

# EDP parabólicas d2u/dx2  = K du/dt
# método explícito,usando diferencias divididas
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
# Valores de frontera
Ta = 1
Tb = 0
#T0 = 25
fx = lambda x: np.cos(3*np.pi/2*x)
# longitud en x
a = 0
b = 1
# Constante K
K = 2
# Tamaño de paso
dx = 0.2
dt = dx/100
# iteraciones en tiempo
n = 10

# PROCEDIMIENTO
# iteraciones en longitud
xi = np.arange(a,b+dx,dx)
fi = fx(xi)
m = len(xi)
ultimox = m-1

# Resultados en tabla u[x,t]
u = np.zeros(shape=(m,n), dtype=float)

# valores iniciales de u[:,j]
j=0
ultimot = n-1
u[0,:]= Ta
u[1:ultimox,j] = fi[1:ultimox]
u[ultimox,:] = Tb

# factores P,Q,R
lamb = dt/(K*dx**2)
P = lamb
Q = 1 - 2*lamb
R = lamb

# Calcula U para cada tiempo + dt
j = 0
while not(j>=ultimot): # igual con lazo for
    for i in range(1,ultimox,1):
        u[i,j+1] = P*u[i-1,j] + Q*u[i,j] + R*u[i+1,j]
    j=j+1

# SALIDA
print('Tabla de resultados')
np.set_printoptions(precision=2)
print(u)

# Gráfica
salto = int(n/10)
if (salto == 0):
    salto = 1
for j in range(0,n,salto):
    vector = u[:,j]
    plt.plot(xi,vector)
    plt.plot(xi,vector, '.r')
    
plt.xlabel('x[i]')
plt.ylabel('t[j]')
plt.title('Solución EDP parabólica')
plt.show()