s2Eva_2023PAOI_T3 EDP elíptica, placa rectangular con frontera variable

Ejercicio: 2Eva_2023PAOI_T3 EDP elíptica, placa rectangular con frontera variable

Dada la EDP elíptica,

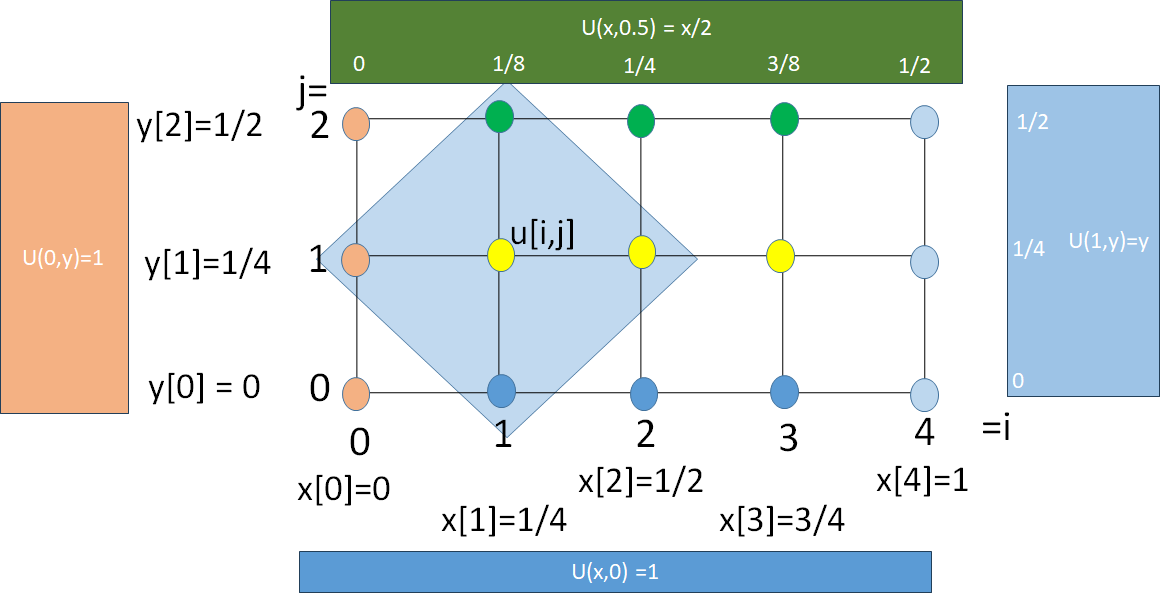
\frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2} = \Big( x^2 + y^2 \Big) e^{xy}

0 \lt x \lt 1

0 \lt y \lt 0.5

Se convierte a la versión discreta usando diferencias divididas centradas, según se puede mostrar con la gráfica de malla.

literal b

literal a

\frac{u[i-1,j]-2u[i,j]+u[i+1,j]}{\Delta x^2} +

+ \frac{u[i,j-1]-2u[i,j]+u[i,j+1]}{\Delta y^2} = \Big( x^2 + y^2 \Big) e^{xy}

literal c

Se agrupan los términos Δx, Δy semejante a formar un λ al multiplicar todo por Δy²

\frac{\Delta y^2}{\Delta x^2}\Big(u[i-1,j]-2u[i,j]+u[i+1,j] \Big) +

+ \frac{\Delta y^2}{\Delta y^2}\Big(u[i,j-1]-2u[i,j]+u[i,j+1]\Big) = \Big( x^2 + y^2 \Big) e^{xy}\frac{\Delta y^2}{\Delta x^2}

los tamaños de paso en ambos ejes son de igual valor, se simplifica la ecuación

\lambda= \frac{\Delta y^2}{\Delta x^2} = 1

se simplifica el coeficiente en λ =1

u[i-1,j]-2u[i,j]+u[i+1,j] +

+ u[i,j-1]-2u[i,j]+u[i,j+1] = \Big( x^2 + y^2 \Big) e^{xy}

Se agrupan los términosiguales

u[i-1,j]-4u[i,j]+ u[i+1,j] + u[i,j-1] +u[i,j+1]

= \Big( x^2 + y^2 \Big) e^{xy}

Se desarrollan las iteraciones para tres rombos y se genera el sistema de ecuacioens a resolver.
para i=1,j=1

u[0,1]-4u[1,1]+ u[2,1] + u[1,0] +u[1,2]

= \Big( x[1]^2 + y[1]^2 \Big) e^{x[1]y[1]}

1-4u[1,1]+ u[2,1] + 1 + \frac{1}{8}

= \Big( 0.25^2 + 0.25^2 \Big) e^{(0.25) (0.25)}

-4u[1,1]+ u[2,1] = \Big( 0.25^2 + 0.25^2 \Big) e^{(0.25) (0.25)} - \frac{1}{8}

para i=2, j=1

u[1,1]-4u[2,1]+ u[3,1] + u[2,0] +u[2,2]

= \Big( x[2]^2 + y[1]^2 \Big) e^{x[2]y[1]}

u[1,1]-4u[2,1]+ u[3,1] + 1 + 0.25

= \Big( 0.5^2 + 0.25^2 \Big) e^{(0.5)(0.25)}

u[1,1]-4u[2,1]+ u[3,1] = \Big( 0.5^2 + 0.25^2 \Big) e^{(0.5)(0.25)} -1.25

para i=3, j=1

u[2,1]-4u[3,1]+ u[4,1] + u[3,0] +u[3,2]

= \Big( x[3]^2 + y[1]^2 \Big) e^{x[3]y[1]}

u[2,1]-4u[3,1]+ 0.25 + 0 + \frac{3}{8}

= \Big( 0.75^2 + 0.25^2 \Big) e^{(0.75)(0.25)}

u[2,1]-4u[3,1] = \Big( 0.75^2 + 0.25^2 \Big) e^{(0.75)(0.25)} - 0.25 - \frac{3}{8}

con lo que se puede crear un sistema de ecuaciones y resolver el sistema para cada punto desconocido

\begin{pmatrix} -4 & 1 & 0 & \Big| & 0.008061807364732415 \\ 1 & -4 & 1 & \Big| & -0.8958911084166168 \\0 & 1 & -4 &\Big| & 0.1288939058881129 \end{pmatrix}

se obtiene los resultados para:

u[1,1] = 0.05953113
u[2,1] = 0.24618634
u[3,1] = 0.02932311

>>> import numpy as np
>>> (0.25**2+0.25**2)*np.exp(0.25*0.25) - 1/8
0.008061807364732415
>>> (0.5**2+0.25**2)*np.exp(0.5*0.25) - 1.25
-0.8958911084166168
>>> (0.75**2+0.25**2)*np.exp(0.75*0.25) - 0.25 -3/8
0.1288939058881129
>>> A=[[-4,1,0],[1,-4,1],[0.0,1.0,-4.0]]
>>> B = [0.008061807364732415, -0.8958911084166168, 0.1288939058881129]
>>> np.linalg.solve(A,B)
array([0.05953113, 0.24618634, 0.02932311])