Ejercicio: 2Eva_2025PAOI_T1 coordenadas centroide por integración numérica
Para el integral con Qy use fórmulas de Simpson con al menos 3 tramos,
Q_y = \int x dA = \int_0^5 x^3 dxa. Para el intervalo de integración [0,5], al considerar 3 tramos, h = 5/3 que es mayor que 1. Se prefiere h≤1 de tal forma que al calcular los errores, la cota del error disminuya por estar en el orden O(hk), por lo que tramos será al menos 5 obteniendo h=1.
xi = [ 0, 1, 2, 3, 4, 5]
c. Con 5 tramos, 6 muestras, se usarán Simpson de 3/8 y luego Simpson de 1/3.
I_{3/8} = \frac{3}{8} (1) \left( 0^3+3(1^3)+3(2^3)+3^3\right) = 20.25 I_{1/3} = \frac{1}{3} (1) \left( 3^3+4(4^3)+5^3\right) = 136d. Q_y =I_{3/8} + I_{1/3} = 20.25+136 =156.25
cota de error = O(h5)+O(h5) = 2[ O(h5)] = 2(15) = 2
Fórmulas compuestas, tramos: 5 métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado tramos iguales en xi: [3 0 0 2 0 0] ['S38', 20.25] ['S13', 136.0] tramos iguales en xi: [3 0 0 2 0 0] Integral: 156.25
Para el integral con Qx use Cuadratura de Gauss de dos puntos
Q_x = \int ydA = \int_0^5 \frac{x^4}{2} dxb. Para cuadratura de Gauss, se tomarían al menos 3 tramos, dado que la cota de error por truncamiento se aproxima con la ≅ f(4)( x )
xi = [ 0, 5/3, 10/3, 5]
c. intervalo [0, 5/3]
x_a = \frac{5/3+0}{2} - \left( \frac{1}{\sqrt{3}} \right) \frac{5/3-0}{2} =0.352208 x_b = \frac{5/3+0}{2} + \left( \frac{1}{\sqrt{3}}\right) \frac{5/3-0}{2} =1.314458 I_0 = \frac{5/3-0}{2} \left( f(x_a) +f(1.314458) \right) = \frac{5/3-0}{2} \left( \frac{(0.352208)^4}{2} +\frac{(1.314458) ^4}{2} \right) = 1.2502d. usando el algoritmo se puede obtener el resultado de:
[xa,xb,f(xa),f(xb)],area [0.352208, 1.314458, 0.007694, 1.492648] 1.250285 [xa,xb,f(xa),f(xb)],area [2.018874, 2.981125, 8.306298, 39.490340] 39.830532 [xa,xb,f(xa),f(xb)],area [3.685541, 4.647791, 92.251874, 233.322542] 271.312014 Integral: 312.39283264746234
Para el integral de área A:
se plantea usando Simpson de 3/8 o cualquier otro método numérico. con h=1
xi = [ 0, 1, 2, 3, 4, 5]
A = \int f(x) dx = \int_0^5 x^2 dx I_{3/8} = \frac{3}{8} (1) \left( 0^2+3(1^2)+3(2^2)+3^2\right) = 9 I_{1/3} = \frac{1}{3} (1) \left( 3^2+4(4^2)+5^2\right) = 32.6666d. Q_y =I_{3/8} + I_{1/3} = 9+32.6666 =41.6666
cota de error = O(h5)+O(h5) = 2[ O(h5)] = 2(15) = 2
usando el algoritmo se obtiene:
Fórmulas compuestas, tramos: 5 métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado tramos iguales en xi: [3 0 0 2 0 0] ['S38', 9.0] ['S13', 32.666666666666664] tramos iguales en xi: [3 0 0 2 0 0] Integral: 41.666666666666664
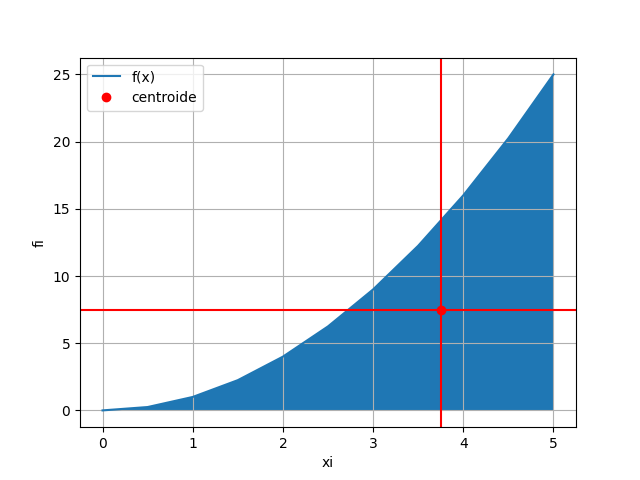
e. Determine las coordenadas del centroide según las fórmulas presentadas.
\bar{x} = \frac{Q_y}{A}= \frac{156.25}{41.6666} = 3.75 \bar{y} = \frac{Q_x}{A}= \frac{312.5}{41.6666} = 7.5
literal f se deja como tarea.