Ejercicio: 2Eva_IIT2019_T2 EDO, problema de valor inicial
la ecuación del problema planteado es:
y'(t) = f(t,y) = \frac{y}{2t^3}0 ≤ t ≤ 1
y(0.5) = 1.5
literal a
La solución empieza usando la Serie de Taylor por ejemplo para tres términos:
y_{i+1} = y_{i} + h y'_i + \frac{h^2}{2!} y''_i x_{i+1} = x_{i} + h E = \frac{h^3}{3!} y'''(z) = O(h^3)Se observa que se tiene el valor inicial y la primera derivada, si usamos tres términos se puede usar la segunda derivada.
y'(t) = f(t,y) = \frac{y}{2t^3} y''(t) = f'(t,y) = \frac{y'}{2t^3} + y \Big(\frac{-3}{2t^4}\Big) y''(t) = \frac{1}{2t^3}\Big( \frac{y}{2t^3} \Big) - \frac{3y}{2t^4} y''(t) = \frac{y}{4t^6} -\frac{3y}{2t^4}por lo que la ecuación de Taylor a usar queda de la siguiente forma:
y_{i+1} = y_{i} + h y'_i + \frac{h^2}{2!} y''_i y_{i+1} = y_{i} + h\frac{y}{2t^3}+\frac{h^2}{2} \Big( \frac{y}{4t^6} -\frac{3y}{2t^4}\Big)que es la ecuacion que se usará con un error de O(h3)
Reemplazando los valores en la fórmula se obtiene la siguiente tabla:
estimado [ti, yi, d1yi, d2yi] [[ 0.5 1.5 6. -12. ] [ 0.6 2.04 4.7222 -12.68004115] [ 0.7 2.4488 3.5697 -10.09510219] [ 0.8 2.7553 2.6907 -7.46259891] [ 0.9 2.9870 2.0487 -5.42399041] [ 1. 3.1648 0. 0. ]]
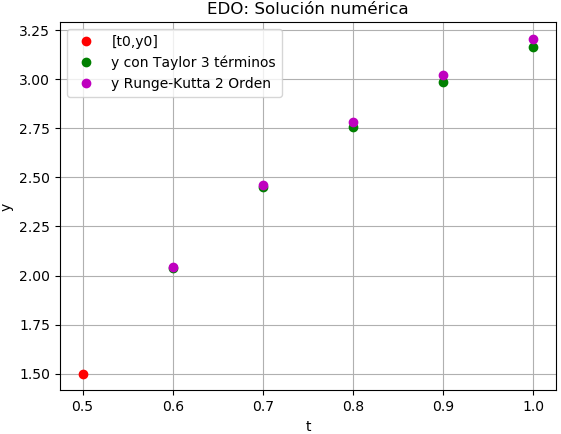
cuya gráfica es:
literal b
Para desarrollar Runge-Kutta de 2do orden se dispone de los siguientes datos:
y'(t) = f(t,y) = \frac{y}{2t^3}t0 = 0.5, y0 = 1.5, h = 0.1
pasos del algoritmo,
K_1 = h * y'(t_i) K_2 = h * y'(t_i+h, y_i + K_1) y_{i+1} = y_i + \frac{K_1+K_2}{2} t_i = t_i + h</p> <p>iteración 1: i = 0
K_1 = 0.1 * y'(0.5) = 0.6 K_2 = 0.1 * y'(0.5+0.1, 1.5 + 0.6) = 0.4861 y_{1} = 1.5 + \frac{0.6+0.4861}{2} = 2.0430 t_1 = 0.5 + 0.1 = 0.6</p> <p>iteración 2: i = 1
K_1 = 0.1 * y'(0.6) = 0.4729 K_2 = 0.1 * y'(0.6+0.1, 2.0430 + 0.4729) = 0.3667 y_{1} = 2.0430 + \frac{0.4729+0.3667}{2} = 2.4629 t_1 = 0.6 + 0.1 = 0.7</p> <p>iteración 3: i = 2
K_1 = 0.1 * y'(0.7) = 0.3590 K_2 = 0.1 * y'(0.7+0.1, 2.4629 + 0.3590) = 0.3667 y_{1} = 2.4629 + \frac{0.3590+0.3667}{2} = 2.7802 t_1 = 0.7 + 0.1 = 0.8</p> <p>obteniendo la siguiente tabla:
estimado [ti, yi, K1, K2] [[0.5 1.5 0. 0. ] [0.6 2.0430 0.6 0.4861] [0.7 2.4629 0.4729 0.3667] [0.8 2.7802 0.3590 0.2755] [0.9 3.0206 0.2715 0.2093] [1. 3.2048 0.2071 0.1613]] Diferencias entre Taylor y Runge-Kutta2 [ 0. -0.0030 -0.0140 -0.0248 -0.0335 -0.0400]
Algoritmo en Python
# EDO. Método de Taylor 3 términos # Runge-Kutta de 2 Orden # 2Eva_IIT2019_T2 EDO, problema de valor inicial import numpy as np # Funciones desarrolladas en clase def edo_taylor3t(d1y,d2y,x0,y0,h,muestras): tamano = muestras + 1 estimado = np.zeros(shape=(tamano,4),dtype=float) # incluye el punto [x0,y0] estimado[0] = [x0,y0,0,0] x = x0 y = y0 for i in range(1,tamano,1): estimado[i-1,2:]= [d1y(x,y),d2y(x,y)] y = y + h*d1y(x,y) + ((h**2)/2)*d2y(x,y) x = x+h estimado[i,0:2] = [x,y] return(estimado) def rungekutta2(d1y,x0,y0,h,muestras): tamano = muestras + 1 estimado = np.zeros(shape=(tamano,4),dtype=float) # incluye el punto [x0,y0] estimado[0] = [x0,y0,0,0] xi = x0 yi = y0 for i in range(1,tamano,1): K1 = h * d1y(xi,yi) K2 = h * d1y(xi+h, yi + K1) yi = yi + (K1+K2)/2 xi = xi + h estimado[i] = [xi,yi,K1,K2] return(estimado) # PROGRAMA PRUEBA # INGRESO # d1y = y', d2y = y'' d1y = lambda t,y: y/(2*t**3) d2y = lambda t,y: y/(4*t**6)-(3/2)*y/(t**4) t0 = 0.5 y0 = 1.5 h = 0.1 muestras = 5 # PROCEDIMIENTO # Edo con Taylor puntos = edo_taylor3t(d1y,d2y,t0,y0,h,muestras) ti = puntos[:,0] yi = puntos[:,1] # Runge-Kutta puntosRK2 = rungekutta2(d1y,t0,y0,h,muestras) # ti = puntosRK2[:,0] # lo mismo del anterior yiRK2 = puntosRK2[:,1] # diferencias diferencia = yi-yiRK2 # SALIDA print('estimado[ti, yi, d1yi, d2yi]') print(puntos) print('estimado[ti, yi, K1, K2]') print(puntosRK2) print('Diferencias entre Taylor y Runge-Kutta2') print(diferencia) # Gráfica import matplotlib.pyplot as plt plt.plot(ti[0],yi[0],'o', color='r', label ='[t0,y0]') plt.plot(ti[1:],yi[1:],'o', color='g', label ='y con Taylor 3 términos') plt.plot(ti[1:],yiRK2[1:],'o', color='m', label ='y Runge-Kutta 2 Orden') plt.title('EDO: Solución numérica') plt.xlabel('t') plt.ylabel('y') plt.legend() plt.grid() plt.show())