Ejercicio: 2Eva_IT2012_T1_MN Longitud de teleférico
Los datos tomados para el problema son:
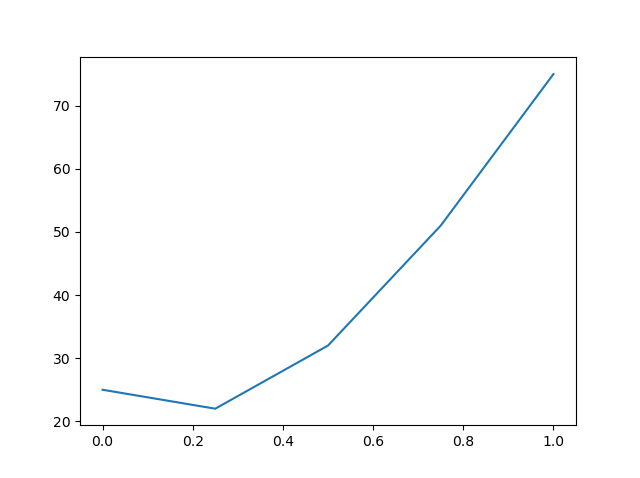
x = [0.00, 0.25, 0.50, 0.75, 1.00] f(x) = [25.0, 22.0, 32.0, 51.0, 75.0]
Se debe considerar que los datos tienen tamaño de paso (h) del mismo valor.
Literal a)
Fórmulas de orden 2, a partir de:
https://blog.espol.edu.ec/analisisnumerico/formulas-de-diferenciacion-por-diferencias-divididas/
considere que el término del Error O(h2), perdió una unidad del exponente en el proceso, por lo que las fórmulas de orden 2 tienen un error del mismo orden.
Se puede usar por ejemplo:
Para los términos x en el intervalo [0,0.50] hacia adelante
f'(x_i) = \frac{-f(x_{i+2})+4f(x_{i+1})-3f(x_i)}{2h} + O(h^2)Para el término x con 0.75, centradas:
f'(x_i) = \frac{f(x_{i+1})-f(x_{i-1})}{2h} + O(h^2)y para el término x con 1.0, hacia atras:
f'(x_i) = \frac{3f(x_{i})-4f(x_{i-1})+f(x_{i-2})}{2h} + O(h^2)Luego se aplica el resultado en la fórmula:
g(x) = \sqrt{1+[f'(x)]^2}L = \int_a^b g(x) \delta x .
Literal b)
Use las fórmulas de integración numérica acorde a los intervalos. Evite repetir intervalos, que es el error más común.
Por ejemplo, se puede calcular el integral de g(x) aplicando dos veces Simpson de 1/3, que sería la más fácil de aplicar dado los h iguales.
Otra opción es Simpson de 3/8 añadido un trapecio, otra forma es solo con trapecios en todo el intervalo.
Como ejemplo de cálculo usando un algoritmo en Python se muestra que:
f'(x): [-38. 22. 66. 86. 106.] g(x): [ 38.0131 22.0227 66.0075 86.0058 106.0047] L con S13: 59.01226169578733 L con trapecios: 61.511260218050175
los cálculos fueron realizados a partir de la funciones desarrolladas durante la clase. Por lo que se muestran 3 de ellas en el algoritmo.
import numpy as np import matplotlib.pyplot as plt # Funciones para integrar realizadas en clase def itrapecio (datos,dt): n=len(datos) integral=0 for i in range(0,n-1,1): area=dt*(datos[i]+datos[i+1])/2 integral=integral + area return(integral) def isimpson13(f,h): n = len(f) integral = 0 for i in range(0,n-2,2): area = (h/3)*(f[i]+4*f[i+1]+f[i+2]) integral = integral + area return(integral) def isimpson38 (f,h): n=len(f) integral=0 for i in range(0,n-3,3): area=(3*h/8)*(f[i]+3*f[i+1]+3*f[i+2] +f[i+3] ) integral=integral + area return(integral) # INGRESO x = np.array( [0.0,0.25,0.50,0.75,1.00]) fx= np.array([ 25.0, 22.0, 32.0, 51.0, 75.0]) # PROCEDIMIENTO n = len(fx) dx = x[1]-x[0] # Diferenciales dy = np.zeros(n) for i in range(0,n-2,1): dy[i] = (-fx[i+2]+4*fx[i+1]-3*fx[i])/(2*dx) # Diferenciales penúltimo i = n-2 dy[i] = (fx[i+1]-fx[i-1])/(2*dx) # Diferenciales último i = n-1 dy[i] = (3*fx[i]-4*fx[i-1]+fx[i-2])/(2*dx) # Función gx gx = np.sqrt(1+(dy**2)) # Integral integral = isimpson13(gx,dx) integrartr = itrapecio(gx,dx) # SALIDA print('f\'(x):', dy) print(' g(x):', gx) print("L con S13: ", integral ) print("L con trapecios: ", integrartr ) plt.plot(x,fx) plt.show()