Ejercicio: 3Eva_IIT2018_T2 Drenar tanque cilíndrico
La ecuación a desarrollar es:
\frac{\delta y}{\delta t} = -k\sqrt{y}con valores de k =0.5, y(0)=9
Formula de Taylor con término de error:
P_{n}(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} (x-x_0)^k P_{n}(x) = f(x_0)+\frac{f'(x_0)}{1!} (x-x_0) + + \frac{f''(x_0)}{2!}(x-x_0)^2 + + \frac{f'''(x_0)}{3!}(x-x_0)^3 + \text{...}Se requiere la 2da y 3ra derivadas:
\frac{\delta^2 y}{\delta t^2} = -k\frac{1}{2} y^{(\frac{1}{2}-1)} = -\frac{k}{2} y^{-\frac{1}{2}} \frac{\delta^3 y}{\delta t^3} = -\frac{k}{2}\Big(-\frac{1}{2}\Big) y^{(-\frac{1}{2}-1)} = \frac{k}{4} y^{-\frac{3}{2}}con lo que inicia las iteraciones y cálculo del error, con avance de 0.5 para t.
t=0 , y(0) = 9
t = 0.5
\frac{\delta y(0)}{\delta t} = -(0.5)\sqrt{9} = -1.5 \frac{\delta^2 y(0)}{\delta t^2} = -\frac{0.5}{2} 9^{-\frac{1}{2}} = - 0.08333 \frac{\delta^3 y(0)}{\delta t^3} = \frac{0.5}{4} 9^{-\frac{3}{2}} = 0.004628 P_{2}(0.5) = 9 - 1.5 (0.5-0) + \frac{-0.08333}{2}(0.5-0)^2 P_{2}(0.5) = 8.2395Error orden de:
Error = \frac{0.004628}{3!}(0.5-0)^3 = 9.641 . 10^{-5}t = 1
\frac{\delta y(0.5)}{\delta t} = -(0.5)\sqrt{8.2395} = -1.4352 \frac{\delta^2 y(0.5)}{\delta t^2} = -\frac{0.5}{2} (8.2395)^{-\frac{1}{2}} = - 0.08709 \frac{\delta^3 y(0.5)}{\delta t^3} = \frac{0.5}{4} (8.2395)^{-\frac{3}{2}} = 0.005285 P_{2}(1) = 8.2395 - 1.4352(1-0.5) + \frac{-0.08709}{2}(1-0.5)^2 P_{2}(1) = 7.5110Error orden de:
Error = \frac{0.005285}{3!}(1-0.5)^3 = 4.404 . 10^{-4}t = 1.5
\frac{\delta y(1)}{\delta t} = -(0.5)\sqrt{7.5110} = -1.3703 \frac{\delta^2 y(1)}{\delta t^2} = -\frac{0.5}{2} (7.5110)^{-\frac{1}{2}} = - 0.09122 \frac{\delta^3 y(1)}{\delta t^3} = \frac{0.5}{4} (7.5110)^{-\frac{3}{2}} = 0.006072 P_{2}(1.5) = 7.5110 - 1.3703(1.5-1) + \frac{-0.09122}{2}(1.5-1)^2 P_{2}(1.5) = 6.8144Error orden de:
Error = \frac{0.006072}{3!}(1.5-1)^3 = 1.4 . 10^{-4}t = 2
\frac{\delta y(1.5)}{\delta t} = -(0.5)\sqrt{6.8144} = -1.3052 \frac{\delta^2 y(1.5)}{\delta t^2} = -\frac{0.5}{2} (6.8144)^{-\frac{1}{2}} = - 0.09576 \frac{\delta^3 y(1.5)}{\delta t^3} = \frac{0.5}{4} (6.8144)^{-\frac{3}{2}} = 0.007026 P_{2}(2) = 6.8144 - 1.3052 (2-1.5) - \frac{0.09576}{2}(2-1.5)^2 P_{2}(2) = 6.1498Error orden de:
Error = \frac{0.007026}{3!}(2-1.5)^3 = 1.4637 . 10^{-4}Se estima que el próximo término pasa debajo de 6 pies.
Por lo que estima esperar entre 2 y 2.5 minutos.
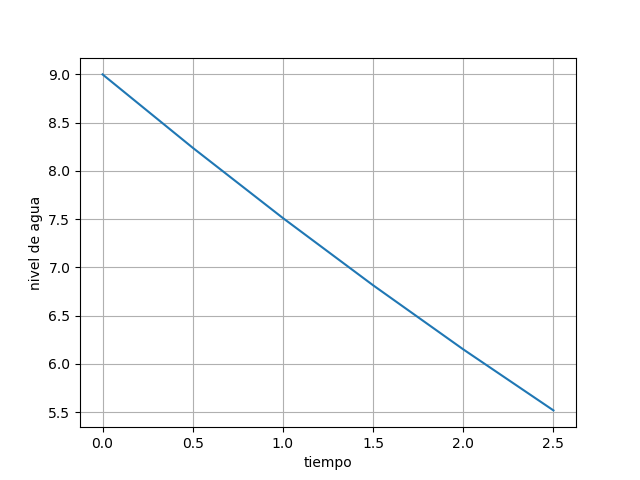
resultados usando el algoritmo:
ti, p_i, error [[0.00000000e+00 9.00000000e+00 0.00000000e+00] [5.00000000e-01 8.23958333e+00 9.64506173e-05] [1.00000000e+00 7.51107974e+00 1.10105978e-04] [1.50000000e+00 6.81451855e+00 1.26507192e-04] [2.00000000e+00 6.14993167e+00 1.46391550e-04] [2.50000000e+00 5.51735399e+00 1.70751033e-04]]
Algoritmo en Python
# 3Eva_IIT2018_T2 Drenar tanque cilíndrico import numpy as np import matplotlib.pyplot as plt # INGRESO y0 = 9 t0 = 0 buscar = 6 k = 0.5 h = 0.5 dy = lambda t,y: -k*np.sqrt(y) d2y = lambda t,y: -(k/2)*(y**(-1/2)) d3y = lambda t,y: (k/4)*(y**(-3/2)) # PROCEDIMIENTO resultado = [[t0,y0,0]] yi = y0 ti = t0 while not(yi<buscar): ti = ti+h dyi = dy(ti,yi) d2yi = d2y(ti,yi) d3yi = d3y(ti,yi) p_i = yi +dyi*(h) + (d2yi/2)*(h**2) errado = (d3yi/6)*(h**3) yi = p_i resultado.append([ti,p_i,errado]) resultado = np.array(resultado) # SALIDA print('ti, p_i, error') print(resultado) # Grafica plt.plot(resultado[:,0],resultado[:,1]) plt.ylabel('nivel de agua') plt.xlabel('tiempo') plt.grid() plt.show()