Ejercicio: 1Eva_IIIT2007_T2 Función Cobb-Douglas
[ a1 interpola filas ] [a2 interpola punto Y] [ b1 interpola columnas ] [ b2 raíz Newton-Raphson] [ Algoritmo ]
..
literal a.1 Interpola tabla por filas
Se usa la tabla para plantear los polinomios usando los datos de cada fila. Se evalúa el polinomio con el valor de K=25 (en miles) para completar los datos de la columna K=25
| L\K (miles $) | 10 | 20 | 25 | 30 | 40 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 10 | 11.0000 | 13.0813 | 14.4768 | 15.5563 | |
| 20 | 18.4997 | 22.0000 | 24.3470 | 26.1626 | |
| 25 | Y | ||||
| 30 | 25.0746 | 29.8189 | 33.0000 | 35.4608 |
Para la fila L=0 no es necesario realizar un polinomio, pues se observa que para 0 trabajadores la producción es nula, no existe producción p(K)=0 y pK(25)=0.
Para la fila L=10, se disponen de 4 puntos, por lo que se plantea un polinomio de grado 3:
P_{L10}(K) = 11\frac{(K-20)(K-30)(K-40)}{(10-20)(10-30)(10-40)} + + 13.0813\frac{(K-10)(K-30)(K-40)}{(20-10)(20-30)(20-40)} + + 14.4768\frac{(K-10)(K-20)(K-40)}{(30-10)(30-20)(30-40)} + + 15.5563\frac{(k-10)(k-20)(k-30)}{(40-10)(40-20)(40-30)}Con el algoritmo se simplifica la expresión:
P_{L10}(K) =0.0000616335 K^3 - 0.0071269*K^2 + 0.378796 K + 7.8630Se evalúa el polinomio con K=25
P_{L10}(K) =0.0000616335 (25)^3 - 0.0071269*(25)^2 + 0.378796 (25) + 7.8630 P_{L10}(25) = 13.84166Se observan los resultados encontrados en la primera gráfica:
Se continua el ejercicio usando los algoritmos para encontrar los polinomios de Lagrange obteniendo:
**** literal a:
Polinomio de Lagrange por fila de L
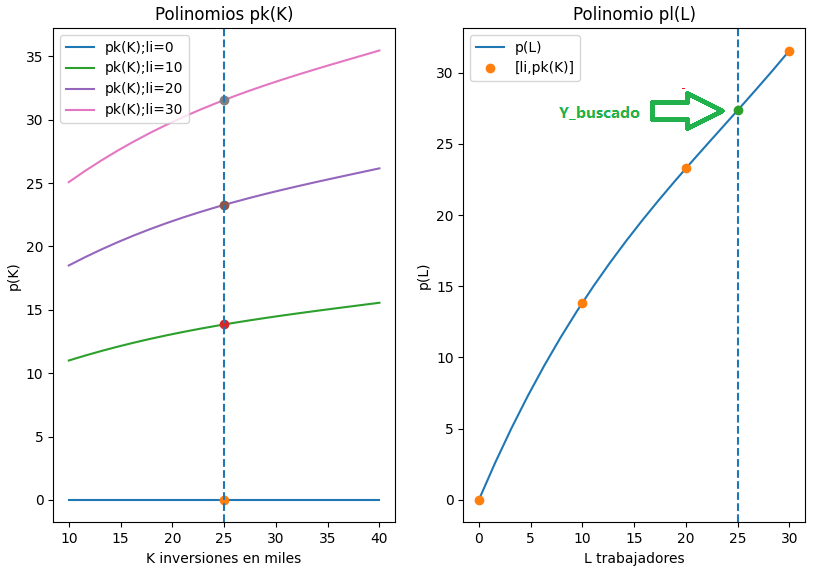
fila: 0 , li[fila]: 0 , polinomio pk :
0
pk[25]: 0
___
fila: 1 , li[fila]: 10 , polinomio pk :
3 2
6.16333333333342e-5*K - 0.00712699999999999*K + 0.378796666666668*K + 7.86309999999999
pk[25]: 13.8416625000000
___
fila: 2 , li[fila]: 20 , polinomio pk :
3 2
0.000103649999999999*K - 0.0119855*K + 0.637039999999995*K + 13.2242
pk[25]: 23.2787937499999
___
fila: 3 , li[fila]: 30 , polinomio pk :
3 2
0.00014048333333333*K - 0.0162449999999998*K + 0.863441666666663*K + 17.9242
pk[25]: 31.5521687500000
___
Datos para el polinomio de L
li:
[ 0 10 20 30]
k_buscado:
[0, 13.8416625000000, 23.2787937499999, 31.5521687500000]
[ a1 interpola filas ] [a2 interpola punto Y] [ b1 interpola columnas ] [ b2 raíz Newton-Raphson] [ Algoritmo ]
literal a.2 Interpola un punto en Y con K=25
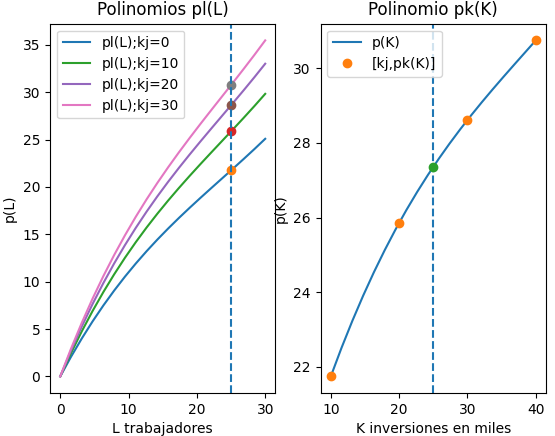
Con los datos obtenidos se genera el siguiente polinomio P(L), que corresponde a la parte derecha de la gráfica mostrada.
P_{k=25}(L) = 0\frac{(L-10)(L-20)(L-30)}{(0-10)(0-20)(0-30)} + + 13.84166\frac{(L-0)(L-20)(L-30)}{(10-0)(10-20)(10-30)} + + 23.27879\frac{(L-0)(L-10)(L-30)}{(20-0)(20-10)(20-30)} + + 31.55216\frac{(L-0)(L-10)(L-20)}{(30-0)(30-10)(30-20)}simplificando con el algoritmo se tiene:
P_{k=25}(L) = 00.00054012 L^3 - 0.038226 L^2 + 1.71241 Levaluando el polinomio con L=25
P_{k=25}(L) = 00.00054012 (25)^3 - 0.038226 (25)^2 + 1.71241 (25) P_{k=25}(L) = 27.358402Con los datos obtenidos se realiza la gráfica en 3D marcando los puntos calculados con los polinomios.
![Cobb Douglas Y[L,K]](https://blog.espol.edu.ec/analisisnumerico/files/2017/11/CobbDouglas01.png)
[ a1 interpola filas ] [a2 interpola punto Y] [ b1 interpola columnas ] [ b2 raíz Newton-Raphson] [ Algoritmo ]
literal b.1 Interpola tabla por columnas
| L\K (miles $) | 10 | 20 | K=? | 30 | 40 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 10 | 11.0000 | 13.0813 | 14.4768 | 15.5563 | |
| 20 | 18.4997 | 22.0000 | 24.3470 | 26.1626 | |
| 25 | Y=30 | ||||
| 30 | 25.0746 | 29.8189 | 33.0000 | 35.4608 |
Se repite el ejercicio del literal a, con el mismo algoritmo para no rescribir todo por las filas por columnas. En el algoritmo se intercambian las filas por columnas y se transpone la matriz.
# INGRESO ... # Se intercambian los valores de fila columna para repetir el algoritmo # obteniendo Y(L=25,k) M = np.transpose(M) kj = [0, 10, 20, 30] li = [10, 20, 30, 40] l_busca = 25 # trabajadores k_busca = 25 # inversión en miles de $
Se ajustan las etiquetas de las gráficas y se obtiene el polinomio a usar, que es la producción Y(k) para un capital K dado:
Y(K) = P_{L=25}(K) =
0.000121812500000016*K**3 - 0.0140857812500013*K**2 +
0.748676562500027*K + 15.5417812499999
Y(K) = 0.00012181 K^3 - 0.014085 K^2 + 0.74867 K + 15.54178
[ a1 interpola filas ] [a2 interpola punto Y] [ b1 interpola columnas ] [ b2 raíz Newton-Raphson] [ Algoritmo ]
literal b.2 raíz con Newton-Raphson
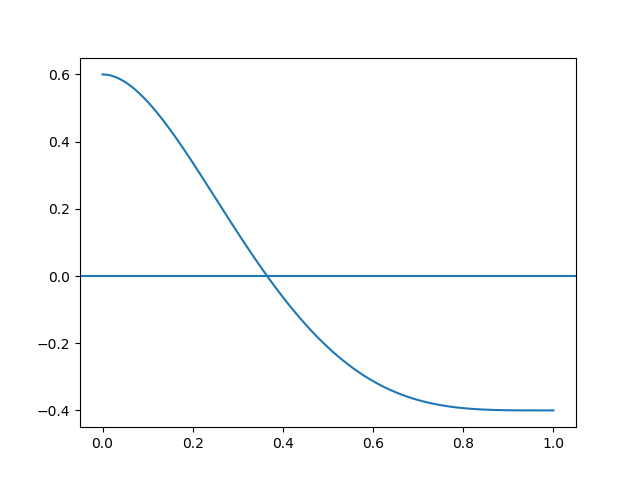
Para el algoritmo de Newton- Raphson, el ejercicio se plantea igualando el polinomio al valor buscado de producción Y=30. Se escribe luego la expresión en como f(x)=0 y f'(x):.
0.00012181 K^3 - 0.014085 K^2 + 0.74867 K + 15.54178 = 30 f(K) = 0.00012181 K^3 - 0.014085 K^2 + 0.74867 K + 15.54178 - 30 f'(K) = 0.0001218(3) K^2 - 0.014085(2) K+ 0.74867 f'(K) = 0.00036543 K^2 - 0.02817 K+ 0.74867Usando la gráfica se inicia con K0=30, por ser el valor mas cercano de los puntos conocidos a Y=30, se obtienen los siguientes resultados:
itera = 0
f(30) = 0.00012181 (30)^3 - 0.014085 (30)^2 + 0.74867 (30) + + 15.54178 - 30 = -1.3862 f'(30) = 0.00036543 (30)^2 - 0.02817 (30)+ 0.74867 = 0.2325 K_{1} = 30 -\frac{-1.3862}{0.2325} = 35.963 errado = |35.963 -30| = 5.963itera = 1
f(35.963) = 0.00012181 (35.963)^3 - 0.014085 (35.963)^2 + + 0.74867 (35.963) + 15.54178 - 30 = -0.0854 f'(35.963) = 0.00036543 (35.963)^2 - 0.02817 (35.963) + 0.74867 = 0.2082 K_{2} = 35.963 -\frac{-0.0854}{0.2082} = 36.3734 errado = |36.3734 -35.963| = 0.4104itera = 2
f( 36.3734) = 0.00012181 ( 36.3734)^3 - 0.014085 ( 36.3734)^2 + + 0.74867 ( 36.3734) + 15.54178 - 30 = -0.00016955 f'( 36.3734) = 0.00036543 ( 36.3734)^2 - 0.02817 ( 36.3734)+ + 0.74867 = 0.20751 K_{3} = 36.3734 -\frac{-0.00016955}{0.20751} = 36.374 errado = |36.374 - 36.3734| = 0.00081705Se observa que el error disminuye en cada iteración, por lo que el método converge.
Se sigue con las iteraciones usando el algoritmo:
método de Newton-Raphson i ['xi', 'fi', 'dfi', 'xnuevo', 'tramo'] 0 [30. -1.3862 0.2325 35.963 5.963 ] 1 [35.963 -0.0854 0.2082 36.3734 0.4104] 2 [ 3.6373e+01 -1.6955e-04 2.0751e-01 3.6374e+01 8.1705e-04] 3 [ 3.6374e+01 -3.8858e-08 2.0751e-01 3.6374e+01 1.8726e-07] raíz en: 36.3742052500759
Se encuentra la raíz en 36.3741, que corresponde a una inversión K un poco mas de 36 mil dólares para una producción Y de 30 mil unidades.
[ a1 interpola filas ] [a2 interpola punto Y] [ b1 interpola columnas ] [ b2 raíz Newton-Raphson] [ Algoritmo ]
Instrucciones en Python. literal a
#1Eva_IIIT2007_T2 Función Cobb-Douglas # Interpolacion de Lagrange import numpy as np import matplotlib.pyplot as plt import sympy as sym def interpola_lagrange(xi,yi): ''' Interpolación con método de Lagrange resultado: polinomio en forma simbólica ''' # PROCEDIMIENTO n = len(xi) x=sym.Symbol('x') # Polinomio polinomio = 0*x # inicializa con cero for i in range(0,n,1): # Termino de Lagrange termino = 1 for j in range(0,n,1): if (j!=i): termino = termino*(x-xi[j])/(xi[i]-xi[j]) polinomio = polinomio + termino*yi[i] # Expande el polinomio polinomio = polinomio.expand() return(polinomio) # INGRESO M = [[ 0, 0, 0, 0 ], [11.0000, 13.0813, 14.4768, 15.5563], [18.4997, 22.0000, 24.3470, 26.1626], [25.0746, 29.8189, 33.0000, 35.4608]] li = [0, 10, 20, 30] kj = [10, 20, 30, 40] l_busca = 25 # trabajadores k_busca = 25 # inversion en miles de $ # PROCEDIMIENTO M = np.array(M) tamano = np.shape(M) n = tamano[0] m = tamano[1] x,K,L = sym.symbols('x,K,L') # Literal a.1 Interpola polinomio pk # por fila de trabajadores L # evalua en k_busca, inversiones en miles poli_fila = [] pk_columna =[] for fila in range(0,n,1): pk = interpola_lagrange(kj,M[fila,:]) pk = pk.subs(x,K) poli_fila.append(pk) pk_busca = poli_fila[fila].subs(K,k_busca) pk_columna.append(pk_busca) # Interpola un polinomio en columna de inversiones pk_columna # evalua en l_busca pkl_busca = interpola_lagrange(li,pk_columna) pkl_busca = pkl_busca.subs(x,L) Ykl_busca = pkl_busca.subs(L,l_busca) # SALIDA np.set_printoptions(precision=4) print(' **** literal a:') print('___ Polinomio por fila de trabajadores L') for fila in range(0,n,1): print(fila,', L['+str(fila)+']=',li[fila], ', pk(K) :') print(poli_fila[fila]) print(' pk['+str(k_busca)+']:',pk_columna[fila]) print('___') print('\n Datos para el polinomio de L') print(' Li: ',li) print('k_busca: ',pk_columna) print('Polinomio p(L):') print(pkl_busca) print('Y[l_busca,k_busca]: ',Ykl_busca) # Grafica de P(k) por cada L muestras = 20 xk = np.linspace(min(kj),max(kj),muestras) plt.subplot(121) for fila in range(0,n,1): pk = poli_fila[fila] if pk.has(K): pk_lambda = sym.lambdify(K,pk) pkx = pk_lambda(xk) else: nk = len(xk) pkx = np.ones(nk)*float(pk) plt.plot(xk,pkx, label='pk(K);li='+str(li[fila])) plt.plot(k_busca,pk_columna[fila],'o') plt.ylabel('p(K)') plt.xlabel('K inversiones en miles') plt.axvline(k_busca, linestyle ='dashed') plt.title('Polinomios pk(K)') plt.legend() # Grafica de p(L) en k_busca xl = np.linspace(min(li),max(li),muestras) pl_lambda = sym.lambdify(L,pkl_busca) plx = pl_lambda(xl) plt.subplot(122) plt.plot(xl,plx, label='p(L)') plt.plot(li,pk_columna,'o', label='[li,pk(K)]') plt.axvline(l_busca, linestyle ='dashed') plt.plot(l_busca,Ykl_busca,'o') plt.ylabel('p(L)') plt.xlabel('L trabajadores') plt.title('Polinomio pl(L)') plt.legend() # plt.show() # Grafica 3D from mpl_toolkits.mplot3d import axes3d X, Y = np.meshgrid(kj,li) figura = plt.figure() ax = figura.add_subplot(111, projection = '3d') ax.plot_wireframe(X,Y,M) ax.plot(k_busca,l_busca,Ykl_busca,'o',label='(25,25,Y)') ax.plot(k_busca*np.ones(len(li)),li,pk_columna,'o') ax.set_xlabel('K inversion') ax.set_ylabel('L trabajadores') ax.set_zlabel('Y producción') ax.set_title('Cobb-Douglas') plt.show()
[ a1 interpola filas ] [a2 interpola punto Y] [ b1 interpola columnas ] [ b2 raíz Newton-Raphson] [ Algoritmo ]
Instrucciones en Python. literal b
#1Eva_IIIT2007_T2 Función Cobb-Douglas # Interpolacion de Lagrange # Newton-Raphson import numpy as np import matplotlib.pyplot as plt def newton_raphson(fx,dfx,xi, tolera, iteramax=100, vertabla=False, precision=4): ''' funciónx y fxderiva en forma numérica lambda xi es el punto inicial de búsqueda ''' itera=0 tramo = abs(2*tolera) if vertabla==True: print('i', ['xi','fi','dfi', 'xnuevo', 'tramo']) np.set_printoptions(precision) while (tramo>=tolera and itera<iteramax): fi = fx(xi) dfi = dfx(xi) xnuevo = xi - fi/dfi tramo = abs(xnuevo-xi) if vertabla==True: print(itera,np.array([xi,fi,dfi,xnuevo,tramo])) xi = xnuevo itera = itera + 1 if itera>=iteramax: xi = np.nan print('itera: ',itera, 'No converge,se alcanzó el máximo de iteraciones') return(xi) # INGRESO y_busca = 30 fx = lambda K: 0.0001218125*K**3 - 0.0140857812500013*K**2 + 0.748676562500027*K + 15.5417812499999 -y_busca dfx = lambda K: 0.00036543*K**2 - 0.02817*K + 0.748676562500027 x0 = 30 tolera = 0.00001 muestras = 20 # PROCEDIMIENTO respuesta = newton_raphson(fx,dfx,x0, tolera, vertabla=True) # SALIDA print('raíz en: ', respuesta) # Grafica xl = np.linspace(0,40,muestras) plx = fx(xl) plt.plot(xl,plx, label='Y(k)') plt.axhline(0,linestyle='dotted') plt.ylabel('f(K)') plt.xlabel('K inversiones en miles') plt.title('f(K) = Y(K)-'+str(y_busca)) plt.show()
[ a1 interpola filas ] [a2 interpola punto Y] [ b1 interpola columnas ] [ b2 raíz Newton-Raphson] [ Algoritmo ]
