Ejercicio: 3Eva_IT2019_T2 Integral con interpolación
El ejercicio considera dos partes: interpolación e integración
a. Interpolación
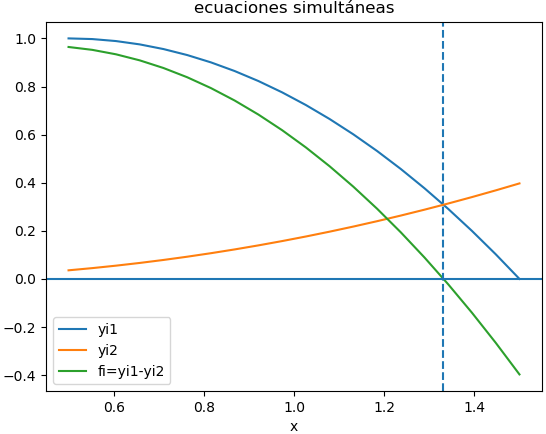
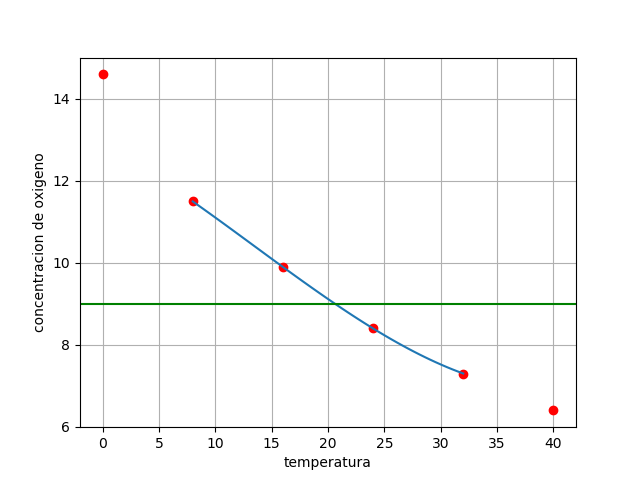
Se requiere aproximar la función usando tres puntos. Para comprender la razón del método solicitado, se compara la función con dos interpolaciones:
a.1 Lagrange
a.2 Trazador cúbico sujeto
Observando la gráfica se aclara que en éste caso, una mejor aproximación se obtiene con el método de trazador cúbico sujeto. Motivo por lo que el tema tiene un peso de 40/100 puntos
Los valores a considerar para la evaluación son:
puntos referencia xi,yi:
[0. 0.78539816 1.57079633]
[ 0. 0.62426595 -0.97536797]
derivadas en los extremos:
3.141592653589793
0.6929852019184021
Polinomio de Lagrange
-1.80262534301178*x**2 + 2.21061873102778*x
Trazadores cúbicos sujetos
[0. 0.78539816]
-0.548171611756137*x**3 - 2.55744517923506*x**2 + 3.14159265358979*x
[0.78539816 1.57079633]
4.66299098804068*x**3 - 14.8359577843727*x**2 + 12.7851139029174*x - 2.52466795930204
------------------
Valores calculados para Trazadores cúbicos sujetos:
Matriz A:
[[-0.26179939 -0.13089969 0. ]
[ 0.78539816 3.14159265 0.78539816]
[ 0. 0.13089969 0.26179939]]
Vector B:
[ 2.34675256 -16.9893436 2.72970237]
coeficientes S:
[-5.11489036 -7.69808822 14.27573913]
coeficientes a,b,c,d
[-0.54817161 4.66299099]
[-2.55744518 -3.84904411]
[ 3.14159265 -1.89005227]
[0. 0.62426595]
b. Integración
Como forma de comparacíon de resultados, se requiere integrar con varios métodos para comparar resultados y errores.
b.1 Integración con Cuadratura de Gauss, usando el resultado de trazador cúbico.
Se integra en cada tramo de cada polinomio:
Trazadores cúbicos sujetos [0. 0.78539816] -0.548171611756137*x**3 - 2.55744517923506*x**2 + 3.14159265358979*x
Se obtienen los puntos del método de cuadratura desplazados en el rango:
xa: 0.16597416116944688 xb: 0.6194240022280014 area: 0.5037962958529855
Para el segundo tramo:
[0.78539816 1.57079633] 4.66299098804068*x**3 - 14.8359577843727*x**2 + 12.7851139029174*x - 2.52466795930204 xa: 0.9513723245668951 xb: 1.4048221656254496 area: -0.2706563884589365
Con lo que el integral total es:
Integral total: 0.23313990739404894
b.2 Integración analítica
\int_0^{\pi /2}sin(\pi x) dxu = πx
du/dx = π
dx = du/π
se convierte en:
\frac{1}{\pi}\int sin(u) du \frac{1}{\pi}(-cos(u))volviendo a la variable x:
\frac{1}{\pi}(-cos(\pi x)) \Big\rvert_{0}^{\frac{\pi}{2}} -\frac{1}{\pi}(cos(\pi \frac{\pi}{2})-cos(\pi(0))) = 0.24809580527879377c. Estimación del error
Se restan los resultados de las secciones b.1 y b.2
error = |0.24809580527879377 - 0.23313990739404894 |
error = 0.014955897884744829
Algoritmo en Python
separado por literales
# 3Eva I T 2019 Interpola e Integra import numpy as np import sympy as sym import matplotlib.pyplot as plt def interpola_lagrange(xi,yi): ''' Interpolación con método de Lagrange resultado: polinomio en forma simbólica ''' # PROCEDIMIENTO n = len(xi) x = sym.Symbol('x') # Polinomio polinomio = 0 for i in range(0,n,1): # Termino de Lagrange termino = 1 for j in range(0,n,1): if (j!=i): termino = termino*(x-xi[j])/(xi[i]-xi[j]) polinomio = polinomio + termino*yi[i] # Expande el polinomio polinomio = polinomio.expand() return(polinomio) def traza3sujeto(xi,yi,u,v): ''' Trazador cúbico sujeto, splines resultado: polinomio en forma simbólica ''' n = len(xi) # Valores h h = np.zeros(n-1, dtype=float) # Sistema de ecuaciones A = np.zeros(shape=(n,n), dtype=float) B = np.zeros(n, dtype=float) S = np.zeros(n-1, dtype=float) # coeficientes a = np.zeros(n-1, dtype=float) b = np.zeros(n-1, dtype=float) c = np.zeros(n-1, dtype=float) d = np.zeros(n-1, dtype=float) polinomios=[] if (n>=3): for i in range(0,n-1,1): h[i]=xi[i+1]-xi[i] A[0,0] = -h[0]/3 A[0,1] = -h[0]/6 B[0] = u-(yi[1]-yi[0])/h[0] for i in range(1,n-1,1): A[i,i-1] = h[i-1] A[i,i] = 2*(h[i-1]+h[i]) A[i,i+1] = h[i] B[i] = 6*((yi[i+1]-yi[i])/h[i] - (yi[i]-yi[i-1])/h[i-1]) A[n-1,n-2] = h[n-2]/6 A[n-1,n-1] = h[n-2]/3 B[n-1] = v-(yi[n-1]-yi[n-2])/h[n-2] # Resolver sistema de ecuaciones S = np.linalg.solve(A,B) # Coeficientes for i in range(0,n-1,1): a[i]=(S[i+1]-S[i])/(6*h[i]) b[i]=S[i]/2 c[i]=(yi[i+1]-yi[i])/h[i]-(2*h[i]*S[i]+h[i]*S[i+1])/6 d[i]=yi[i] # polinomio en forma simbólica x=sym.Symbol('x') polinomios=[] for i in range(0,n-1,1): ptramo = a[i]*(x-xi[i])**3 + b[i]*(x-xi[i])**2 + c[i]*(x-xi[i])+ d[i] ptramo = ptramo.expand() polinomios.append(ptramo) parametros = [A,B,S,a,b,c,d] return(polinomios, parametros) # INGRESO f = lambda x: np.sin(np.pi*x) muestrasf = 20 a = 0 b = np.pi/2 # Derivadas en los extremos u = np.pi*np.cos(np.pi*a) v = np.pi*np.cos(np.pi*b) muestras = 3 # literal a # PROCEDIMIENTO xif = np.linspace(a,b,muestrasf) yif = f(xif) xi = np.linspace(a,b,muestras) yi = f(xi) # Usando Lagrange x = sym.Symbol('x') pL = interpola_lagrange(xi,yi) pxL = sym.lambdify(x,pL) pxiL = pxL(xif) # Trazador cúbico sujeto pS, parametros = traza3sujeto(xi,yi,u,v) pxiS = np.zeros(muestrasf,dtype=float) # Evalua trazadores cúbicos sujetos i=0 ap = xi[i] bp = xi[i+1] poli = sym.lambdify(x, pS[i]) for j in range(0,muestrasf,1): punto = xif[j] if (punto>bp): i = i+1 ap = xi[i] bp = xi[i+1] poli = sym.lambdify(x,pS[i]) pxiS[j] = poli(punto) # SALIDA print('puntos referencia xi,yi: ') print(xi) print(yi) print('derivadas en los extremos: ',u,v) print('Polinomio de Lagrange') print(pL) print('Trazadores cúbicos sujetos') n = len(xi) for i in range(0,n-1,1): print(xi[i:i+2]) print(pS[i]) # Parametros de Trazadores cúbicos sujetos print('Matriz A: ') print(parametros[0]) print('Vector B: ') print(parametros[1]) print('coeficientes S: ') print(parametros[2]) print('coeficienetes a,b,c,d') print(parametros[3]) print(parametros[4]) print(parametros[5]) print(parametros[6]) # Gráficas plt.plot(xif,yif, label='funcion') plt.plot(xi,yi,'o', label='muestras') plt.plot(xif,pxiL, label='p(x)_Lagrange') plt.plot(xif,pxiS, label='p(x)_Traza3Sujeto') plt.legend() plt.xlabel('x') plt.show() # literal b # cuadratura de Gauss de dos puntos def integraCuadGauss2p(funcionx,a,b): x0 = -1/np.sqrt(3) x1 = -x0 xa = (b+a)/2 + (b-a)/2*(x0) xb = (b+a)/2 + (b-a)/2*(x1) area = ((b-a)/2)*(funcionx(xa) + funcionx(xb)) print('xa: ',xa) print('xb: ',xb) print('area: ', area) return(area) # INGRESO f0 = sym.lambdify(x,pS[0]) f1 = sym.lambdify(x,pS[1]) # Procedimiento I0 = integraCuadGauss2p(f0,xi[0],xi[1]) I1 = integraCuadGauss2p(f1,xi[1],xi[2]) It = I0+I1 # SALIDA print('Integral 1: ', I0) print('Integral 2: ', I1) print('Integral total: ',It)