1ra Evaluación 2025-2026 PAO I. 1/Julio/2025
Tema 3 (30 puntos) El avistamiento de ballenas es una actividad popular en Ecuador que atrae a miles de turistas cada año.
 Puerto López, en la provincia de Manabí, a 219 kilómetros de Guayaquil, es uno de los epicentros de esta actividad.
Puerto López, en la provincia de Manabí, a 219 kilómetros de Guayaquil, es uno de los epicentros de esta actividad.
Esta pequeña localidad costera celebra anualmente el Festival de Observación de Ballenas Jorobadas.
El evento busca promover el turismo y la importancia de la conservación marina.
Usando los registros de coordenadas (relativas x,y)donde se han observado las ballenas, realice el trazado de una ruta de avistamiento turístico siguiendo el viaje de las ballenas.
Los puntos registrados son:
| x | 1.03 | 2.2 | 3.6 | 4.24 | 5.3 |
| y | -0.5 | 0.7 | 4.1 | 2.3 | 0.1 |
a. Describa el planteamiento del ejercicio, justificando el grado del polinomio seleccionado.
b. Realice el desarrollo analítico para la ruta de avistamiento, usando interpolación de Lagrange
c. Presente el polinomio simplificado usando el algoritmo.
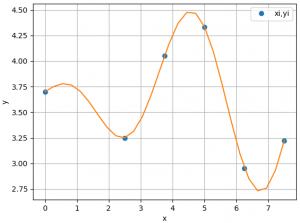
d. Verifique que el polinomio pasa por los puntos usados para el planteamiento usando una gráfica. Observe y comente sus resultados
e. Adjunte algoritmo.py, resultados.txt y gráfica.png en “aulavirtual”.
Rúbrica: literal a (5 puntos), literal b (10 puntos), literal c (5 puntos), literal d (5 puntos), literal e (5 puntos)
xi = [ 1.03, 2.2, 3.6, 4.24, 5.3] yi = [-0.5 , 0.7, 4.1, 2.3, 0.1]
Referencia: [1] Turistas asombrados por avistamiento de ballena blanca en la costa de Ecuador. Teleamazonas.com. 24-junio-2025 https://www.teleamazonas.com/tendencias/turistas-asombrados-avistamiento-ballena-blanca-costa-ecuador-97688/
[2] El impresionante viaje de las ballenas jorobadas a Ecuador. Yalilé Loaiza, Infobae. 30 junio 2024. https://www.infobae.com/america/america-latina/2024/06/30/el-impresionante-viaje-de-las-ballenas-jorobadas-a-ecuador/
[3] Primer avistamiento de una ballena blanca en Ecuador. Televistazo-Ecuavisa. 24-Junio-2025.
[4] Inicia temporada de avistamiento de ballenas en la costa. Televistazo-Ecuavisa.18-junio-2024.