1ra Evaluación 2022-2023 PAO II. 22/Noviembre/2022
Tema 1 (35 puntos) Según el principio de Arquímedes, la fuerza de flotación o empuje es igual al peso de el fluido desplazado por la porción sumergida de un objeto. 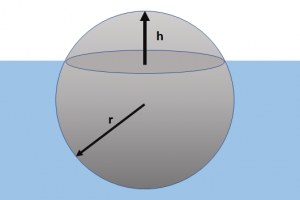
Para la esfera de la figura, determine la altura h de la porción que se encuentra sobre el agua considerando las constantes con los valores mostrados.
ρesfera = 200 Kg/m3
ρagua = 1000 kg/m3
r = 1 m
g =9.8 m/s2
Observe que la porción del volumen sobre el agua de la esfera puede ser determinado como la fórmula presentada.
Fempuje = ρagua Vsumergido g
Fpeso = ρesfera Vesfera g
Para el desarrollo del ejercicio use el método del punto fijo.
Rúbrica: Planteamiento (5 puntos), iteraciones con el error (15 puntos), análisis de la convergencia (10 puntos). observación de resultados (5 puntos).
Referencia:
[1] Ejercicio 5.19. p143 Steven C. Chapra. Numerical Methods 7th Edition.
[2] Fuerza de empuje y flotación. Ingenia UdeA. 29 Abril 2015
[3] Problema - Principio de Arquímedes y fuerza de empuje (Archimedes' principle - problem). Problemas de Física.13 octubre 2019.