Algoritmos 101

Cursos Python

Categoría: 1ra Evaluación

  • 1Eva_IIT2004_T3 Estimar π por Montecarlo

    Parcial  II Término 2004 - 2005, Diciembre, 2004 /ICM00794

    Tema 3. (25 puntos) Encuentre un valor aproximado de la constante π con el siguiente procedimiento. 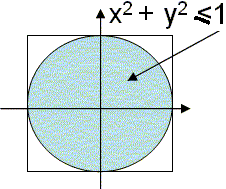circulo centrado en origen de radio 1

    Considere un círculo de radio unitario, centrado en el origen e inscrito en un cuadrado:

    Dado el valor n, genere las coordenadas x, y para n puntos.

    Asigne valores aleatorios reales entre 0 y 1 y cuente cuantos puntos caen dentro del cuadrante de círculo.

    Si llamamos a este contador k, se puede establecer la siguiente relación aproximada suponiendo n grande:

    \frac{k}{n} = \frac{\frac{1}{4} \text{del área del círculo}}{\frac{1}{4} \text{del área del cuadrado}} \frac{\frac{1}{4}\pi(1)^2}{\frac{1}{4} (2)^2}=\frac{\pi}{4} \frac{k}{n} =\frac{\pi}{4}

    Donde se puede obtener el valor aproximado de π a partir de k y n.

    Rúbrica: Puntos de coordenadas aleatorias dentro del cuadrado (5 puntos), verificar punto dentro del círculo (5 puntos), conteo de puntos dentro del círculo (5 puntos), calcular el valor de π (5 puntos). Algoritmo estructurado (5 puntos)

    Referencia:  Fontana di Trevi, https://es.wikipedia.org/wiki/Fontana_di_Trevi

  • 1Eva_IIT2004_T2 Apuestas a números con dados

    Parcial II Término 2004 – 2005. Diciembre, 2004 /ICM00794

    Tema 2. (25 puntos) Simule en un algoritmo el juego descrito entre dos personas: A y B. dado
    Muestre cuál jugador gana el juego y cuántos turnos se tuvieron que jugar.

    • Inicialmente cada una tiene $20
    • En cada turno se lanza un dado
    • Si sale 6 o 4, A gana $3 y B pierde $3
    • Si sale 2, ninguno gana ni pierde
    • Si sale 1, A pierde $6 y B gana $6
    • Si sale 3 o 5, A pierde $1 y B gana $1

    El juego termina cuando una de las dos personas pierde todo su dinero.

  • 1Eva_IIT2004_T1 Nicómano de Gerasa

    Parcial II Término 2004 – 2005. Diciembre, 2004 /ICM00794

    Para cada tema describa un algoritmo con un Diagrama de Flujo, Seudolenguaje , o Matlab

    Tema 1. (25 puntos) Nicómano de Gerasa descubrió la siguiente propiedad de los números naturales:

    Al sumar el primer impar se obtiene el primer cubo: 1 = 1
    Al sumar los dos siguientes impares se obtiene el segundo cubo: 3+5 = 8
    Al sumar los tres siguientes impares se obtiene el tercer cubo: 7+9+11 = 27
    Al sumar los cuatro siguientes impares se obtiene el cuarto cubo: 13+15+17+19 = 64 Etc…

    Con esta propiedad, para un n dado, calcule y muestre los cubos de los primeros n números naturales.

  • 1Eva_IT2004_T4 Verificar matriz simétrica

    Parcial I Término 2004 – 2005. Julio 06, 2004 /ICM00794

    Tema 4. (25 puntos) Se dice que una matriz cuadrada A de orden n es simétrica, si se cumple que:

    ∀ i, ∀j
    (aij = aji)
    1 ≤ i ≤n
    1 ≤ j ≤n    		 1 2 3 4
    2 1 5 6
     3 5 1 7
    4 6 7 1

    Escriba un algoritmo que permita ingresar los elementos de una matriz A con un orden n≤10 y verifique si la matriz es simétrica.

    La matriz presentada es simética respecto a la diagonal, es decir matriz[f,c] = matriz[c.f]

    Nota: símbolo ∀ "Para todo"

    import numpy as np
matriz = [[1,2,3,4],
          [2,1,5,6],
          [3,5,1,7],
          [4,6,7,1]]

matriz = np.array(matriz,dtype=float)

    El resultado debería mostrar:

    "Es simétrica"
>>>

    Si usa la matriz:

    matriz = [[1,4,3,2],
          [2,1,5,6],
          [3,5,1,7],
          [4,6,7,1]]

matriz = np.array(matriz,dtype=float)

    el resultado será:

    "No es simétrica"

  • 1Eva_IT2004_T3 Sortear parejas para tenis

    Parcial I Término 2004 – 2005. Julio 06, 2004 /ICM00794

    Tema 3. (25 puntos) Se tiene una lista de códigos de 25 personas de género masculino numerados del 1 al 25 y otra lista de códigos de 25 personas de género femenino numerados del 26 al 50. tenisjuego

    a) Escriba un algoritmo para sortear parejas mixtas de tenis, tal que a cada persona de género masculino le asigne aleatoriamente una persona de género femenino. Muestre las parejas resultantes.

    b) Muestre los códigos de género femenino que se encuentran en más de una ocasión.

    c) Muestre los códigos de género femenino que no aparecen en asignación alguna.

    Rúbrica:  generación de parejas aleatorias (5 puntos), asignación de parejas en tabla (5 puntos), contar jugadores repetidos (5 puntos),  mostrar jugadores repetidos (5 puntos), mostrar jugadores sin pareja (5 puntos).

  • 1Eva_IT2004_T2 Verificar ISBN

    Parcial I Término 2004 – 2005. Julio 06, 2004 /ICM00794

    Tema 2. (25 puntos) El número estándar internacional de un libro (ISBN: International Standard Book Number) es un código de 10 dígitos. La última cifra es un dígito verificador que indica si el ISBN está correcto. isbn libro

    El dígito verificador es obtenido mediante la operación residuo de S para 11, donde S es la suma de:

    una vez el primer dígito,
    mas dos veces el segundo dígito,
    mas tres veces el tercer dígito,
    . . . ,
    mas nueve veces el noveno dígito.

    Ejemplo:
 la suma S para el ISBN 9684443242 es:
 1*9+2*6+3*8+4*4+5*4+6*4+7*3+8*2+9*4 = 178
 El dígito verificador es el residuo(178/11) 
 que es igual a 2.

    a) Escriba un algoritmo que lea un número ISBN que verifique si éste es o no correcto.

    b) Realice la prueba de escritorio de su algoritmo, utilizando el ISBN 9701702533.

    Referencia: ¿Qué es un ISBN? isbn-international.org. https://www.isbn-international.org/es/content/%C2%BFqu%C3%A9-es-un-isbn

     

  • 1Eva_IT2004_T1 Aleatorios en región sombreada

    Parcial I Término 2004 – 2005. Julio 06, 2004 /ICM00794

    Tema 1. (25 puntos) Escriba un algoritmo que genere aleatoriamente 1000 pares ordenados (x,y), donde x e y son números reales con 2 cifras decimales, tales que: franjaplano

    0.00 ≤ x ≤ 4.00

    0.00 ≤ y ≤ 4.00

    Su algoritmo deberá determinar la cantidad de puntos que se ubicaron dentro de la región sombreada mostrada en la figura.

    Rúbrica: Generar n pares aleatorios (5 puntos), verificar punto debajo de frontera superior (5 puntos), verificar punto por encima de frontera inferior (5 puntos). Conteo de puntos en franja (5 puntos). Algoritmo estructurado (5 puntos)

  • 1Eva_IIIT2003_T4 Dividir Polinomio usando Paolo Ruffini

    Parcial III Término 2003 - 2004. Abril 02, 2004 /ICM00794

    Tema 4. (25 Puntos) La regla de Paolo Ruffini sirve para realizar la división de un polinomio (de grado mayor que 1) para un binomio de la forma (x - a), ambos con coeficientes enteros.

    Al dividir:
    (x3 + 3x2 - x + 1)
    para: (x - 2)

    el coeficiente de la division es: (x2 + 5x + 9)
    y el residuo es: 19

    Escriba un algoritmo en seudo-código que realice lo siguiente:

    a) Permita el ingreso de:

    • El grado n de un polinomio, validando que n sea entero mayor que 1 y menor que 10.
    • Los coeficientes de dicho polinomio en un arreglo de enteros (el orden de ingreso será desde los coeficientes del término de mayor grado hasta el término independiente).
    • El valor de a (entero) del divisor ( x - a )

    b) Muestre por pantalla el resultado de la división (cociente y residuo).

    Rúbrica: validar grado de polinomio (5 puntos), ingreso de coeficientes en arreglo (5 puntos) operaciones (10 puntos),  residuo correcto(5 puntos).

  • 1Eva_IIIT2003_T3 Coordenadas enteras en un círculo

    Parcial III Término 2003 - 2004. Abril 02, 2004 /ICM00794

    Tema 3. (25 puntos) Escriba un algoritmo en seudo-código para determinar el número de puntos del plano cartesiano con coordenadas de valores enteros que pertenecen al círculo limitado por la circunferencia de ecuación

    x^2 + y^2 = 100

    (centro en el origen y radio 10).

    Muestre también el promedio de las distancias de dichos puntos al origen de coordenadas.

    Rúbrica: Manejo de índices enteros como coordenadas (5 puntos). control de intervalos de coordendas en dos dimensiones (5 puntos), manejo de contadores y condicionales (10 puntos), promedio de distancias (5 puntos).

  • 1Eva_IIIT2003_T2 Verificar números triangulares

    Parcial III Término 2003 - 2004. Abril 02, 2004 /ICM00794

    Tema 2. (25 puntos) Considere la secuencia de números triangulares, cuyo nombre refleja su ley de formación:

    1, 3, 6, 10, ...


    Escriba un algoritmo en seudo-código que indique si un número natural t, ingresado por teclado, es triangular.

    Esto es, si es de la forma:

    t = \sum_{i=1}^{n}i

    para algún número natural n

    Rúbrica: identificación de piso en operación (5 puntos), cálculo de usados (5 puntos), control de pisos construidos (5 puntos), validar suma t es triangular (5 puntos), algoritmo estructurado (5 puntos)

    Referencia: Número triangular. Wikipedia