Categoría: Sol_1Eva 2001-2002-2003

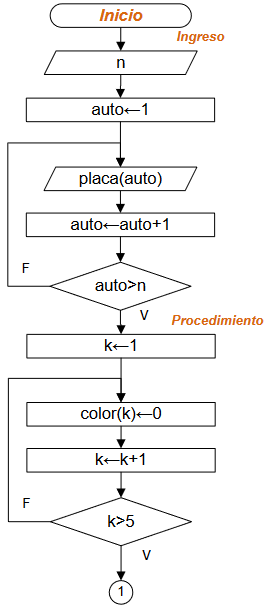
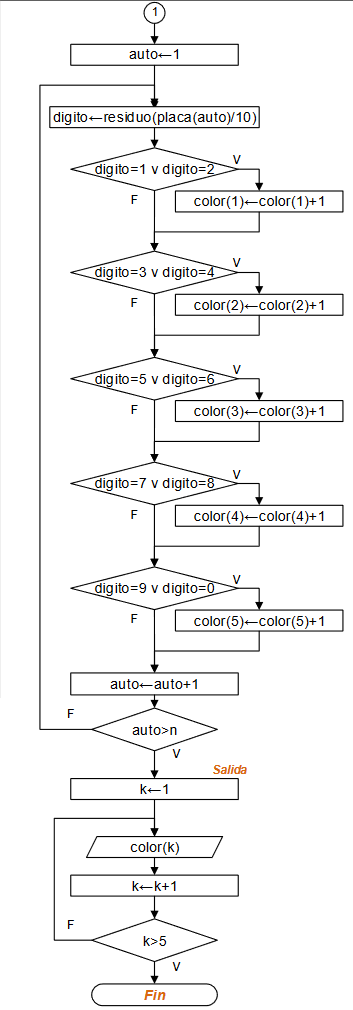
Ejercicio: 1Eva_IIIT2003_T3 Coordenadas enteras en un círculo

Considere el círculo centrado en el origen (0,0),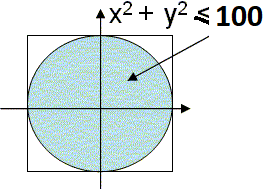 siendo su intervalo entre [-radio, radio].

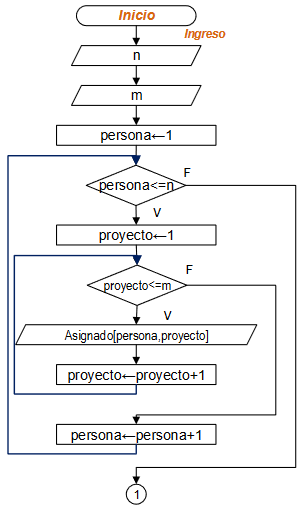
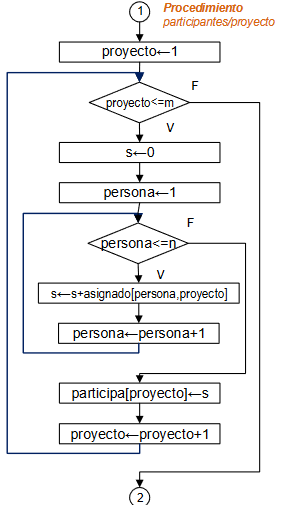
Recorrer las coordenadas de números  enteros en el recuadro limitado por [-radio,radio] en cada lado, determinando la distancia del punto al origen.

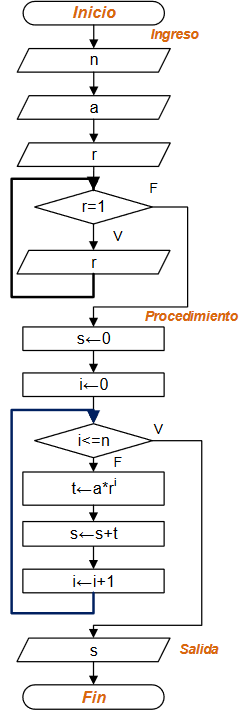
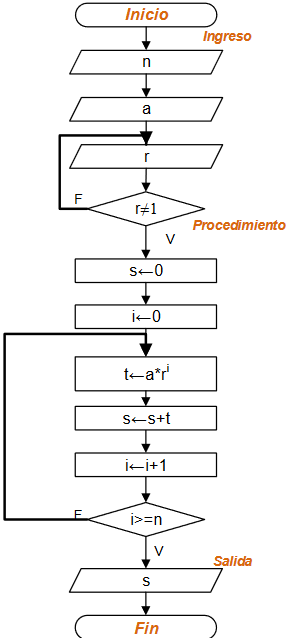
radio = 10
x = [-10, -9, -8, -7, -6 ... 8, 9, 10]

\text{distancia} = \sqrt{x^2+y^2}

dist = np.sqrt(x**2 + y**2)

Con la distancia revisar si el punto está dentro del círculo.

if dist<=radio:
    encirculo = encirculo + 1
    sumadist  = sumadist + dist  

Instrucciones en Python

# 1Eva_IIIT2003_T3 Coordenadas enteras en un círculo
import numpy as np

# INGRESO
radio = 10

# PROCEDIMIENTO
a =  - int(radio)
b = int(radio)

encirculo = 0
sumadist = 0
for y in range(a,b+1,1):
    for x in range(a,b+1,1):
        dist = np.sqrt(x**2 + y**2)
        if dist<=radio:
            encirculo = encirculo + 1
            sumadist  = sumadist + dist          

promdist = sumadist/encirculo
# SALIDA
print(' coordenadas enteras en círculo: ')
print(encirculo)
print('promedio distancias al centro: ')
print(promdist)

resultado:

 coordenadas enteras en círculo: 
317
promedio distancias al centro: 
6.698944789255016
>>> 

Ejercicio: 1Eva_IIT2002_T3 Conjetura de Ullman

Propuesta de solución en Python

Para el número seleccionado o «pensado» se realizan las operaciones paso a paso indicadas en el enunciado.

# INGRESO
n = int(input('piensa un número: '))

Para determinar paridad se obtiene el «residuo» de la división del número para 2 y así decidir cuál operación realizar.

r = n%2

Se sustituye el número por el resultado de la operación y se vuelve a aplicar si el resultado aún no es 1.

    if (r == 0):
        n = n//2
    else:
        n = n*3 + 1

Para conocer el número de operaciones realizadas se usa un contador.

La secuencia se puede almacenar en un vector (lista) para mostrar al final (TAREA)

Se usa un contador de operaciones para la respuesta

El esquema básico del algoritmo en Python es el siguiente:

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2002_T3 Conjetura de Ullman
# propuesta: edelros@espol.edu.ec
# Tarea: convertir a función

# INGRESO
n = int(input('piensa un número: '))

# PROCEDIMIENTO
contar = 0
while not(n==1):
    r = n%2
    
    if (r == 0):
        n = n//2
    else:
        n = n*3 + 1
    print(n)
    contar = contar + 1

# SALIDA
print('operaciones realizadas: ', contar)

Ejercicio: 1Eva_IIT2003_T3 Personas asignadas a proyectos

Propuesta de solución en Python: py_pdf, también propuesta en matlab: m_pdf

Ingresar los datos en una matriz, de tamaño nxm, considerando en las filas a las personas y en las columnas a los proyectos.

Para la parte b), realizar la cuenta de personas asignadas al primer proyecto. Cada resultado por columna de proyecto, se guarda como parte de un vector de participa[proyecto].

El vector de participantes es el resultado de la suma de cada columna.

Para la parte c), se requiere encontrar la carga[persona], que es la suma de cada fila. Por lo que se fija el valor de una persona, una fila, y se revisa para cada persona, todas las columnas, el valor se acumula en «carga».

Se muestra solo aquellas personas que tienen carga de trabajo 0.

Tarea: Validar los datos quese ingresan a la matriz Asigna[persona,proyecto]. Desarrollar la parte para c)

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2003_T3 Personas asignadas a proyectos
# Propuesta: edelros@espol.edu.ec
# Tarea: validar los datos de asignado

import numpy

# INGRESO
n = int(input('cuantas personas: '))
m = int(input('cuantos proyectos: '))
asignado = numpy.zeros((n+1,m+1),dtype=int)
persona = 1
while (persona<=n):
    proyecto = 1
    while (proyecto<=m):
        print('persona: '+str(persona)+
              ', proyecto: '+
              str(proyecto))
        asignado[persona,proyecto] = int(input(' /asignado (1/0): '))
        proyecto = proyecto + 1
    persona = persona+1

# PROCEDIMIENTO
# participantes por proyecto
participan = numpy.zeros(m+1,dtype=int)
proyecto = 1
while (proyecto<=m):
    s = 0
    persona = 1
    while (persona<=n):
        s = s + asignado[persona,proyecto]
        persona = persona+1
    participan[proyecto] = s
    proyecto = proyecto+1

# Carga de trabajo por persona
carga = numpy.zeros(n+1,dtype=int)
persona = 1
while (persona<=n):
    s = 0
    proyecto = 1
    while (proyecto<=m):
        s = s+asignado[persona,proyecto]
        proyecto = proyecto+1
    carga[persona] = s
    persona = persona+1

# SALIDA
print('Participantes/Proyecto:')
proyecto = 1
while (proyecto<=m):
    print(participan[proyecto])
    proyecto = proyecto+1

print('Persona sin carga de trabajo:')
persona = 1
while (persona<=n):
    if carga[persona]==0:
        print(persona)
    persona = persona+1

Ejercicio: 1Eva_IIT2002_T2 Color de placas de vehículos

Propuesta de solución en Python: py_pdf , también en matlab: matlab en pdf

Para el ejercicio se requiere el uso de vectores para almacenar cada placa y procesar los datos en el bloque de procedimiento.

Como todos los datos de entrada se han simplificado a la parte numérica de la placa, se usarán arreglos, aprovechando para practicar con numpy.

En el procedimiento se extrae una placa de un auto para obtener el dígito de las unidades. Con el dígito se puede usar condicionales para indicar cuál es el color que le corresponde y contar la placa de cada color asignado.

dígito	COLOR	¿Cuántos?
1, 2	amarillo (código 1)	…
3, 4	café (código 2)	…
5, 6	rojo (código 3	…
7, 8	azul (código 4)	…
9, 0	verde (código 5)	…

Se continúa con el siguiente auto hasta completar todos los autos registrados en el arreglo.

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2002_T2 Color de placas de vehículos
# propuesta: edelros@espol.edu.ec

import numpy

# INGRESO
n = int(input('cuántos autos: '))

placa = numpy.zeros(n+1,dtype=int)
auto = 1
while not(auto>n):
    print('placa[',auto,']: ')
    placa[auto] = int(input('  : '))
    auto = auto+1

# PROCEDIMIENTO
# contadores por color
color = numpy.zeros(5+1,dtype=int)

# analiza cada auto
auto = 1
while not(auto>n):
    digito = placa[auto]%10
    if (digito==1 or digito==2):
        color[1] = color[1]+1
    if (digito==3 or digito==4):
        color[2] = color[2]+1
    if (digito==5 or digito==6):
        color[3] = color[3]+1
    if (digito==7 or digito==8):
        color[4] = color[4]+1
    if (digito==9 or digito==0):
        color[5] = color[5]+1
    auto = auto+1

# SALIDA
print('Autos por cada color:')
k = 1
while not(k>5):
    print('Color tipo ',k,'= ',color[k])
    k = k+1

Podría intentar realizar el ejercicio con listas, para comparar como se aplican los conceptos.

Tarea: validar que el número de vehículos sea positivo mayor que 0, validar que sean solo tres dígitos en cada placa.

Ejercicio: 1Eva_IIT2003_T4 Juego con icosaedros

Propuesta de solución en Python: py_pdf, también en versión matlab: m_pdf

Se propone desarrollar el tema conociendo el número n de lanzamientos que desea participar el jugador, dejando el control del juego como tarea.

Se inicia un contador de lanzamientos y un acumulador de premios.

Un icosaedro se simula con un aleatorio para el color y otro para el número, para luego comparar éstos valores con lo simulado para el segundo icosaedro.

    d1num   = int(random.random()*5)+1
    d1color = int(random.random()*4)+1
    d2num   = int(random.random()*5)+1
    d2color = int(random.random()*4)+1

Las reglas descritas se implementan con condicionales, considerando que de cumplirse la tercera, ya se ha pagado premio por igualdad de números y color.

    if d1color==d2color:
        premio = premio+10
    if d1num==d2num:
        premio = premio+10
    if ((d1color==d2color)and(d1num==d2num)):
        premio = premio+30

Se repite el juego hasta cumplir el número de lanzamientos.

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2003_T4 Juego con icosaedros
# Propuesta solucion: edelros@espol.edu.ec
# Tarea. Completar el control del juego

import random

# INGRESO
n = int(input('Numero de lanzamientos: '))

# PROCEDIMIENTO
i = 0
premio = 0
while (i<n):
    d1num   = int(random.random()*5)+1
    d1color = int(random.random()*4)+1
    d2num   = int(random.random()*5)+1
    d2color = int(random.random()*4)+1

    if d1color==d2color:
        premio = premio+10
    if d1num==d2num:
        premio = premio+10
    if ((d1color==d2color)and(d1num==d2num)):
        premio = premio+30

    s = d1num+d2num
    r = s%2
    if r>0:
        premio = premio+5

    i = i+1

# SALIDA
print('total ganado: ')
print(premio)
print('lanzamientos: ')
print(n)

Ejercicio: 1Eva_IIT2003_T2 Sumar términos de progresión geométrica

Propuesta de solución en Python: python en pdf, y en versión matlab en pdf

Ingresar la cantidad n de términos, el factor a y r, validando que r no sea 1.

S = \sum_{i=0}^{n} a + ar + ar^2 + ar^3 + ... + ar^n

Iniciar con 0 las variables: s que acumula términos, i como el contador de términos que adicionalmente se usa como exponente.

# PROCEDIMIENTO
s = 0
i = 0
while (i<=n):
    t = a*(r**i)
    s = s + t
    i = i + 1

Como paso siguiente, calcular cada término y acumularlos en s tantas veces como sea necesario hasta que que i llega a n.

El resultado buscado se encontrará en s.

Observe que el primer término es solo la constante a, con equivalente ar⁰.

Lazo mientras-repita:

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2003_T2 Sumar términos de progresión geométrica
# Propuesta de solución. edelros@espol.edu.ec.

# INGRESO
n = int(input('¿Valor de n?: '))
a = float(input('factor a: '))
r = float(input('factor r: '))
while (r==1):
    r = int(input('factor r debe ser diferente de 1: '))

# PROCEDIMIENTO
s = 0
i = 0
while (i<=n):
    t = a*(r**i)
    s = s + t
    i = i + 1

# SALIDA
print(s)

Ejercicio: 1Eva_IIIT2003_T2 Números triangulares

Propuesta de solución en Python: python.pdf , y versión matlab.pdf

El problema planteado es semejante a construir una pirámide, en la que se disponen de solo t bloques y se requiere saber si el número de bloques es exacto para formar una pirámide.

El ejercicio se desarrolla suponiendo que se construirá una pirámide con bloques de varios «pisos».

Se observa que el número de bloques coincide con el número de piso a construir.

Ejemplo:

• Piso 1 tiene 1 bloque,
• piso 2 tiene 2 bloques,
• etc.

Cada piso usa una cierta cantidad de bloques que se cuentan como «usados». La cantidad de bloques por piso es la misma que el número del piso.

El lazo acumula los bloques usados en cada piso.

Dado un número t de bloques ,se calcula la secuencia de números triangulares mientras los bloques usados sean menores que los t disponibles.

En caso que el número “usados” de la secuencia es igual a t, se considera al número t como un número triangular.

La respuesta es un valor de verdad, si es triangular 1, si no lo es 0.

Lazo mientras-repita

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIIT2003_T2 Números triangulares
# Propuesta de solución. edelros@espol.edu.ec

# INGRESO
t=int(input('Verificar si es triangular: '))

# PROCEDIMIENTO
piso = 1
usados = 0
while (usados<t):
    usados = usados+piso
    piso = piso+1

# verifica si es triangular
if usados==t:
    estriangular = 1
else:
    estriangular = 0

# SALIDA
print(estriangular )

Lazo Repita-hasta

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIIT2003_T2 Números triangulares
# Propuesta de solución. edelros@espol.edu.ec

# INGRESO
t = int(input('Verificar si es triangular: '))

# PROCEDIMIENTO
piso = 1
usados = 0
while not(usados>=t):
    usados = usados+piso
    piso = piso+1

# verifica si es triangular
if usados==t:
    estriangular = 1
else:
    estriangular = 0

# SALIDA
print(estriangular )

Ejercicio: 1Eva_IT2001_T5 Verificar divisibilidad para 9

Propuesta de solución en Python: python.pdf, también en versión matlab.pdf

Para la separación de los dígitos de un número entero se usa el residuo de la división para 10.

Por ejemplo:

para el número 15,
el residuo para 10 es 5
y el cociente es 1

La instrucción en Python que obtiene el residuo es

digito = numero%10

y la que obtiene el cociente

numero = numero//10

Una respuesta simplificada es un valor de verdad 1 o 0 para verdadero y falso, que es la que se usa en éste ejemplo.

Lazo mientras-repita

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2001_T5 Verificar divisibilidad para 9
# Propuesta de solución. edelros@espol.edu.ec

# INGRESO
numero = int(input('Número a verificar divisibilidad 9: '))

# PROCEDIMIENTO
sumacifra = 0
# Extrae las cifras
while (numero>0):
    digito    = numero%10
    sumacifra = sumacifra+digito
    numero    = numero//10

if (sumacifra>9):
    numero = sumacifra
    sumacifra = 0
    while (numero>0):
        digito    = numero%10
        sumacifra = sumacifra+digito
        numero    = numero//10

if (sumacifra==9):
    respuesta = 1
else:
    respuesta = 0

# SALIDA
print(respuesta)

lazo repita-hasta

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2001_T5 Verificar divisibilidad para 9
# Propuesta de solución. edelros@espol.edu.ec

# INGRESO
numero=int(input('Numero a verificar divisibilidad 9: '))

# PROCEDIMIENTO
sumacifra=0
# Extrae las cifras
while not(numero==0):
    digito=numero%10
    sumacifra=sumacifra+digito
    numero=numero//10

if (sumacifra>9):
    numero=sumacifra
    sumacifra=0
    while not(numero==0):
        digito=numero%10
        sumacifra=sumacifra+digito
        numero=numero//10

if (sumacifra==9):
    respuesta=1
else:
    respuesta=0

# SALIDA
print(respuesta)

Ejercicio: 1Eva_IIT2002_T4 cociente de Fibonacci

Propuesta de solución en Python:

El ejercicio es una extensión del Algoritmo – Secuencia de Fibonacci, añadiendo la operación del cociente.

Se requiere guardar valores consecutivos del cociente para comparar su diferencia hasta cumplir con la precisión requerida.

Ejemplo de ejecución de algoritmo

>>> 
precision decimal: 0.001
cociente: 0.6181818181818182
con diferencia de:  0.0005347593582887278

Se añade al algoritmo de Fibonacci el cálculo del cociente.

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2002_T4 Cociente de fibonacci
# propuesta: edelros@espol.edu.ec

# INGRESO
precision = float(input('precision decimal: '))

# PROCEDIMIENTO
a = 1 # Primer cociente
b = 1
c = a+b
cociente1 = a/b

a = b # Segundo cociente
b = c
c = a+b
cociente2 = a/b

diferencia = abs(cociente2-cociente1)
while not(diferencia<=precision):
    cociente1 = cociente2
    a = b
    b = c
    c = a+b
    cociente2 = a/b
    diferencia = abs(cociente2-cociente1)

# SALIDA
print('cociente:', cociente2)
print('con diferencia de: ', diferencia)