Ejercicio: 1Eva_IIT2003_T4 Juego con icosaedros
[ algoritmo ] [ diagrama flujo ]
Se propone desarrollar el tema conociendo el número n de lanzamientos que desea participar el jugador, dejando el control del juego como tarea.
Se inicia un contador de lanzamientos y un acumulador de premios.
Un icosaedro se simula con un aleatorio para el color y otro para el número, para luego comparar éstos valores con lo simulado para el segundo icosaedro.
d1num = int(random.random()*5)+1 d1color = int(random.random()*4)+1 d2num = int(random.random()*5)+1 d2color = int(random.random()*4)+1
Las reglas descritas se implementan con condicionales, considerando que de cumplirse la tercera, ya se ha pagado premio por igualdad de números y color.
if d1color==d2color: premio = premio+10 if d1num==d2num: premio = premio+10 if ((d1color==d2color)and(d1num==d2num)): premio = premio+30
Se repite el juego hasta cumplir el número de lanzamientos.
[ algoritmo ] [ diagrama flujo ]
..
Algoritmo en Python
# ICM00794-Fundamentos de Computación - FCNM-ESPOL # 1Eva_IIT2003_T4 Juego con icosaedros # Propuesta solucion: edelros@espol.edu.ec # Tarea. Completar el control del juego import random # INGRESO n = int(input('Numero de lanzamientos: ')) # PROCEDIMIENTO i = 0 premio = 0 while (i<n): d1num = int(random.random()*5)+1 d1color = int(random.random()*4)+1 d2num = int(random.random()*5)+1 d2color = int(random.random()*4)+1 if d1color==d2color: premio = premio+10 if d1num==d2num: premio = premio+10 if ((d1color==d2color)and(d1num==d2num)): premio = premio+30 s = d1num+d2num r = s%2 if r>0: premio = premio+5 i = i+1 # SALIDA print('total ganado: ') print(premio) print('lanzamientos: ') print(n)
[ algoritmo ] [ diagrama flujo ]
..
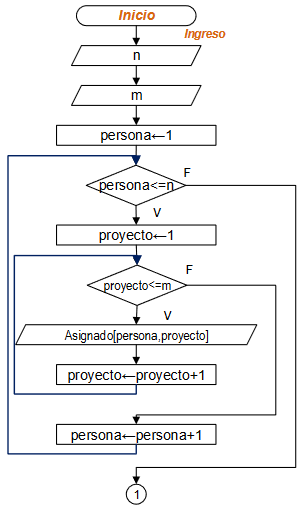
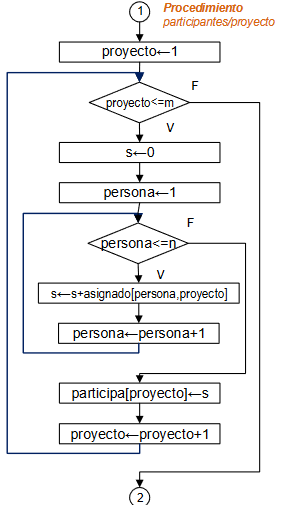
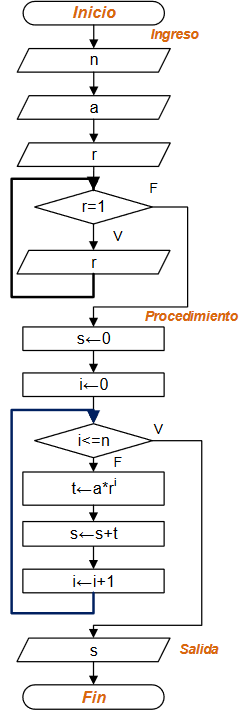
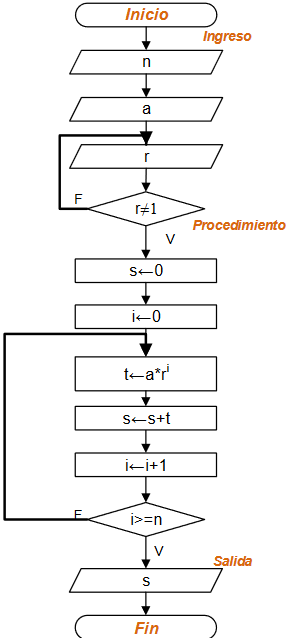
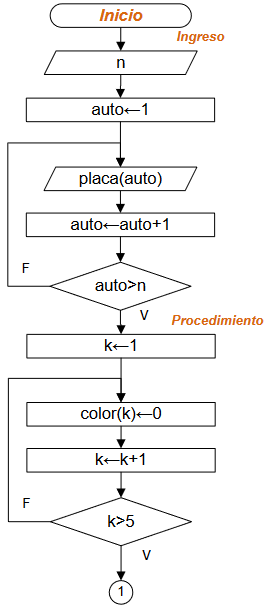
Diagrama de Flujo
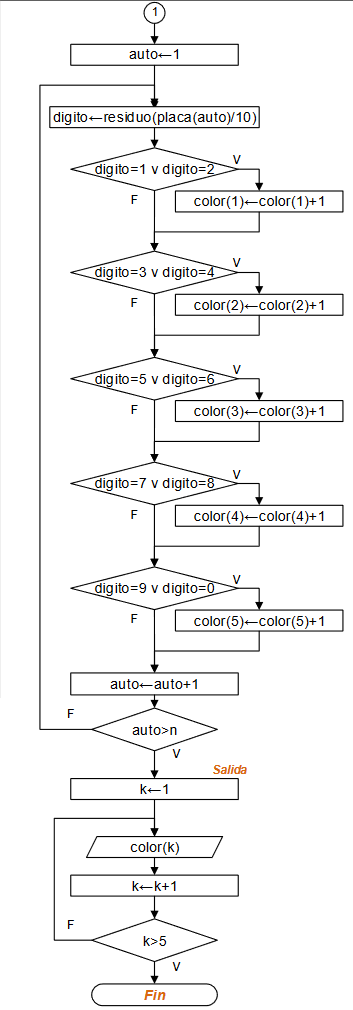
continuación
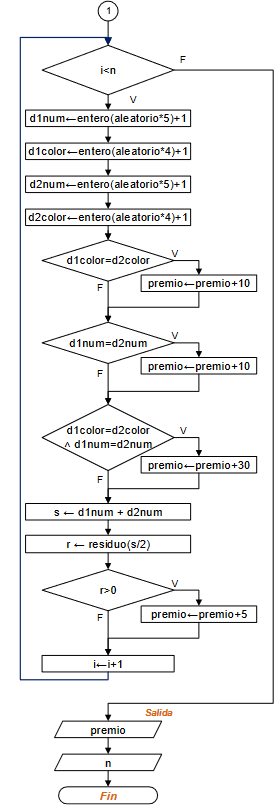
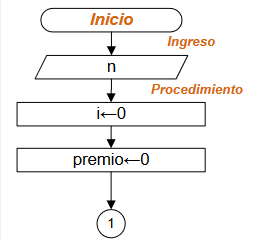
[ algoritmo ] [ diagrama flujo ]
Propuesta de solución con diagrama de flujo: