El curso da una introducción a los conceptos generales de la representación de señales en sistemas continuos y discretos en el dominio del tiempo y frecuencia.
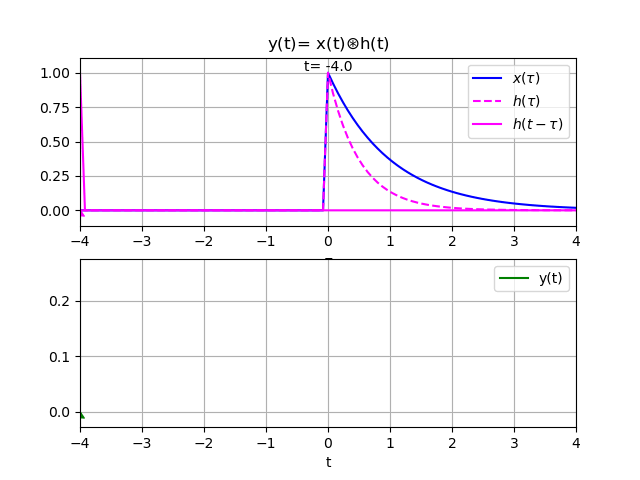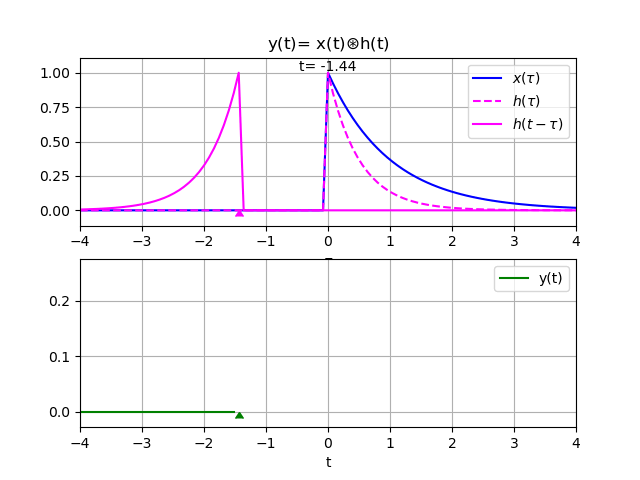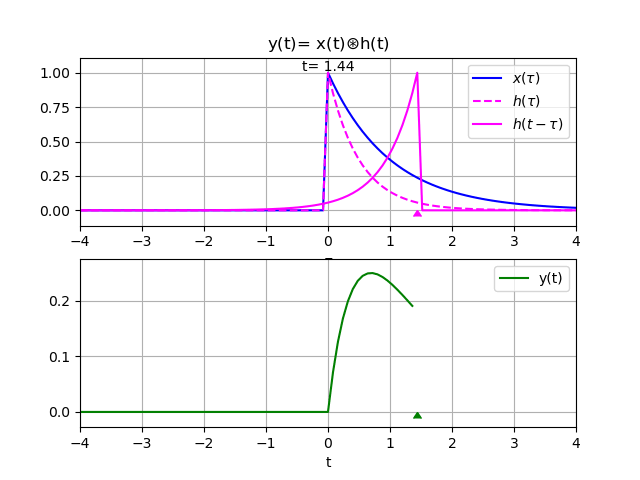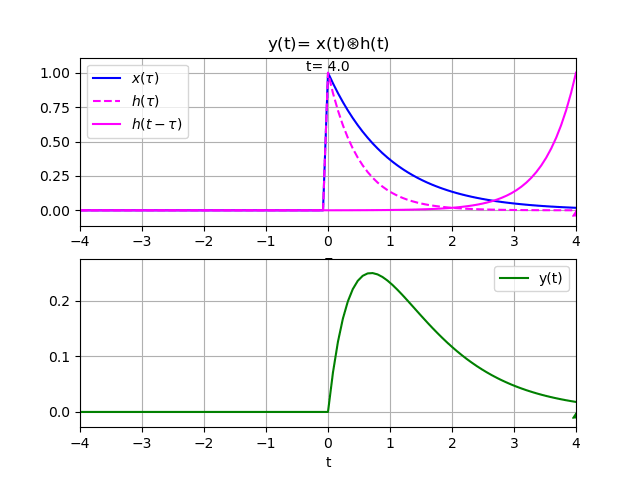
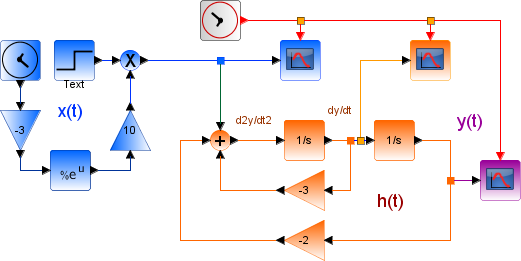
Se plantean soluciones a través de software abierto para cálculo numérico y simbólico con Python y las librerías Sympy, Numpy y Scipy, a la par de cada tema y su solución analítica. De forma complementaria se usa SciLab con Xcos para el manejo de diagrama de bloques.
Contiene material de estudio, problemas y soluciones algorítmicas de las evaluaciones anteriores de los cursos:
- TELG1037 - Señales y Sistemas, desde 2020
- TELG1001 - Señales y Sistemas, 2016-2019
- FIEC05058 - Sistemas Lineales, 2009-2016