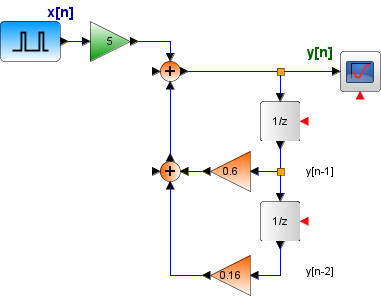
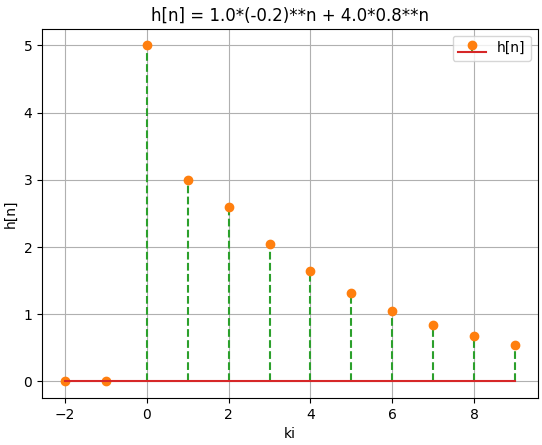
Referencia: Lathi 5.1-1 p495, Oppenheim 10.3 p757
Muchas de las transformadas X[z] de interés práctico son fracciones de polinomios en z, que pueden ser expresadas como una suma de fracciones parciales cuya inversa puede ser revisada en una tabla de transformadas z.
El método de fracciones parciales funciona dado que para cada x[n] transformable con n≥0 le corresponde una X[z] única definida para |z|>a y viceversa. Para lo mostrado, se supone que se usa la fracción parcial mas simple.
Ejemplo 1a. Transformada z inversa de una fracción X[1/z]
Referencia: Oppenheim Ejemplo 10.13 p761, Lathi Ejemplo 5.1 p490
Continuando con el ejercicio presentado para convertir x[n] a X[z], se tiene que:
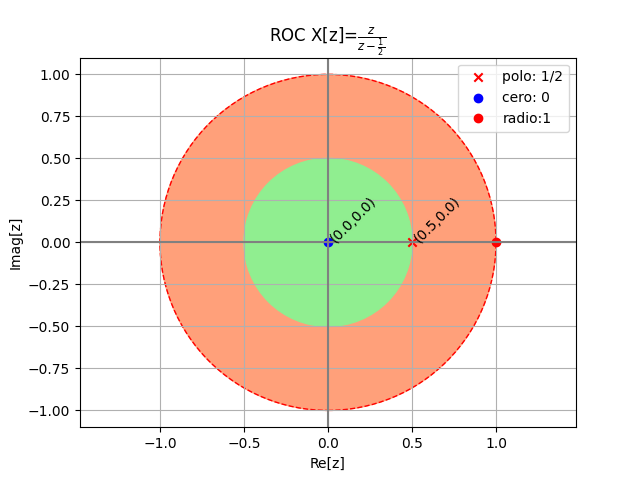
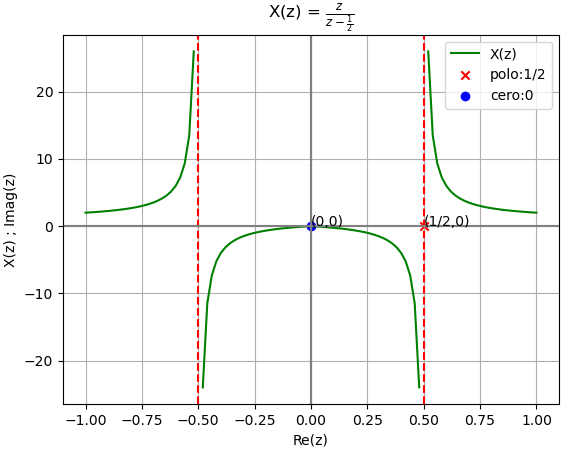
X[z] = \frac{1}{1-a z^{-1}}\text{ , } |z|>|a|la expresión se puede expandir en series se potencias y obtener los primeros términos de la secuencia de x[n]. Los términos son útiles si se se requieren los m primeros términos de la secuencia, es decir n se encuentra en [0,m-1]
X[z]:
z
------
-a + z
F[z]:
2 3 4 5 6
a a a a a a /1 \
1 + - + -- + -- + -- + -- + -- + O|--; z -> oo|
z 2 3 4 5 6 | 7 |
z z z z z \z /
Términos x[n] entre[0,7]
[1, a, a**2, a**3, a**4, a**5, a**6]
x[n] con a= 1/2
[1.0, 0.5, 0.25, 0.125, 0.0625, 0.03125, 0.015625]
Al final de la serie F[z] se muestra un término con el orden del error.
De los términos mostrados, se observa que X[n] = an
Usando por ejemplo a=1/2, se obtiene como resultado de x[n],
>>> xi [1.0, 0.5, 0.25, 0.125, 0.0625, 0.03125, 0.015625]
Ejemplo 1a. Instrucciones Python
# transformada z inversa de X[z] import sympy as sym # INGRESO z = sym.symbols('z',) n = sym.symbols('n', nonnegative=True) a = sym.symbols('a') u = sym.Heaviside(n) Xz = 1/(1-a*z**(-1)) # valor a como racional en dominio 'ZZ' enteros a_k = sym.Rational(1/2).limit_denominator(100) m = 7 # Términos a graficar # PROCEDIMIENTO # Series de potencia z**(-1) Fz = sym.series(Xz,z**(-1), n=m) # Terminos de X[n] xn = [] termino = Fz.args for i in range(0,m,1): xn.append(termino[i]*(z**i)) # SALIDA print('X[z]: ') sym.pprint(Xz) print('\n F[z]:') sym.pprint(Fz) print('\n Términos x[n] entre [0,'+str(m)+']') print(xn) # GRAFICA valores --------------- import numpy as np import matplotlib.pyplot as plt # Terminos de X[n] xi = [] ; ki=[] for i in range(0,m,1): valor = xn[i].subs({z:1,a:a_k}) xi.append(float(valor)) ki.append(i) print('\n x[n] con a=',a_k) print(xi) # grafica entrada x[n] plt.axvline(0,color='grey') plt.stem(ki,xi,label='x[n]') plt.xlabel('n') plt.ylabel('x[n]') plt.title(r'x[n]= $'+str(sym.latex(xn))+'$') plt.grid() plt.show()
Ejemplo 1b. Transformada z inversa de una fracción dada con X[z]
Referencia: Oppenheim Ejemplo 10.13 p761, Lathi Ejemplo 5.1 p490
Si la expresión se usa de la forma simplificada, que es la más común para tratar las expresiones con Sympy, el algoritmo anterior para las series no realiza la misma respuesta.
X[z] = \frac{z}{z-a}\text{ , } \Big|z|>|a| X[z] = \frac{1}{1-a z^{-1}}\text{ , } \Big|z|>|a|Para este caso se multiplica el numerador y denominador por 1/z, obteniendo la expresión del ejemplo anterior. Para generar la serie se realiza el, cambio de variable Z=1/z para generar la serie sobre Z. Luego se restablece en la expresión antes de mostrar los términos, y se obtiene el mismo resultado.
De los términos mostrados, se observa que X[n] = an
Ejemplo 1b. Instrucciones en Python
# transformada z inversa de X[z] # supone que la expresión son fracciones parciales import sympy as sym # INGRESO z = sym.symbols('z') n = sym.symbols('n', integer=True, positive=True) a = sym.symbols('a') Xz = z/(z-a) # valor a como racional en dominio 'ZZ' enteros a_k = sym.Rational(1/2).limit_denominator(100) m = 7 # Términos a graficar # PROCEDIMIENTO # expresión Xz con z para aplicar serie # separa numerador y denominador [Pz,Qz] = Xz.as_numer_denom() Pz = (Pz*(1/z)).expand(1/z) Qz = (Qz*(1/z)).expand(1/z) # cambia Z por 1/z Z = sym.symbols('Z') PZ = Pz.subs(1/z,Z) QZ = Qz.subs(1/z,Z) XZ = PZ/QZ # Series de potencia de Z FZ = sym.series(XZ,Z, n=m) Fz = FZ.subs(Z,1/z) # restituye 1/z # Terminos de X[n] xn = [] termino = Fz.args for i in range(0,m,1): xn.append(termino[i]*(z**i)) # SALIDA print('X[z]: ') sym.pprint(Xz) print('\n F[z]:') sym.pprint(Fz) print('Términos x[n] entre[0,'+str(m)+']') print(xn) # GRAFICA valores --------------- import numpy as np import matplotlib.pyplot as plt # Terminos de X[n] xi = [] ; ki=[] for i in range(0,m,1): valor = xn[i].subs({z:1,a:a_k}) xi.append(float(valor)) ki.append(i) print('\n x[n] con a=',a_k) print(xi) # grafica entrada x[n] plt.axvline(0,color='grey') plt.stem(ki,xi,label='x[n]') plt.xlabel('n') plt.ylabel('x[n]') plt.title(r'x[n]= $'+str(sym.latex(xn))+'$') plt.grid() plt.show()
El algoritmo presentado puede ser tomado como punto de partida para los siguientes ejercicios. Realizado para explicación conceptual.

![Transformada Z Ej01 X[z] x[n]](https://blog.espol.edu.ec/telg1001/files/2017/07/TransformadaZ_Ej01Xz_Xn.png)
![Transformada Z Ej01x[n]](https://blog.espol.edu.ec/telg1001/files/2017/07/TransformadaZ_Ej01xn.png)