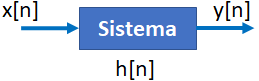
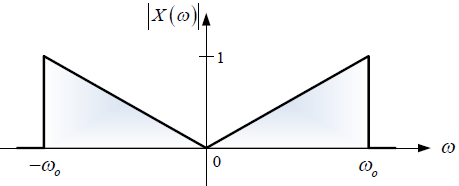
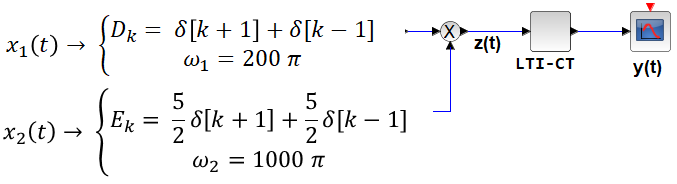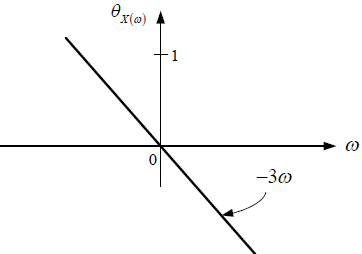Ejercicio: 2Eva2012TI_T3 LTI DT causal, coeficientes de respuesta impulso h[n]
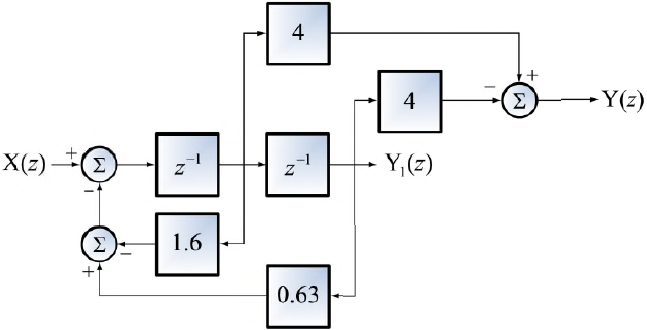
La ecuación de diferencias descrita se usa para crear el diagrama de bloques.
y[n] - \frac{5}{4} y[n-1] + \frac{1}{36} y[n-2] + \frac{1}{18} y[n-3] = x[n] - \frac{1}{2} x[n-1]
literal a. Respuesta impulso h[n]
La forma para usar transformadas z requiere que se desplazar tres unidades.
y[n+3] - \frac{5}{4} y[n+2] + \frac{1}{36} y[n+1] + \frac{1}{18} y[n] = x[n+3] - \frac{1}{2} x[n+2]
z^3 Y[z] - \frac{5}{4} z^2 Y[z] + \frac{1}{36} z Y[z] + \frac{1}{18} Y[z] = z^3X[z] - \frac{1}{2} z^2 X[z]
(z^3 - \frac{5}{4} z^2 + \frac{1}{36} z + \frac{1}{18}) Y[z] = (z^3 - \frac{1}{2} z^2) X[z]
H[z] = \frac{Y[z]}{X[z]} = \frac{z^3 - \frac{1}{2} z^2}{z^3 - \frac{5}{4} z^2 + \frac{1}{36} z + \frac{1}{18}}
las raíces del denominador obtenidas con Sympy-Python:
>>> sym.roots(Pz)
{1/2: 1, 0: 2}
>>> sym.factor(Pz)
z**2*(2*z - 1)/2
>>> sym.factor(Qz)
(4*z - 1)*(9*z**2 - 9*z - 2)/36
>>> sym.roots(Qz)
{1/4: 1, 1/2 - sqrt(17)/6: 1, 1/2 + sqrt(17)/6: 1}
>>>
Observación: existe una raíz con distancia al origen superior al radio=1, por lo que habría un termino creciente no acotado.
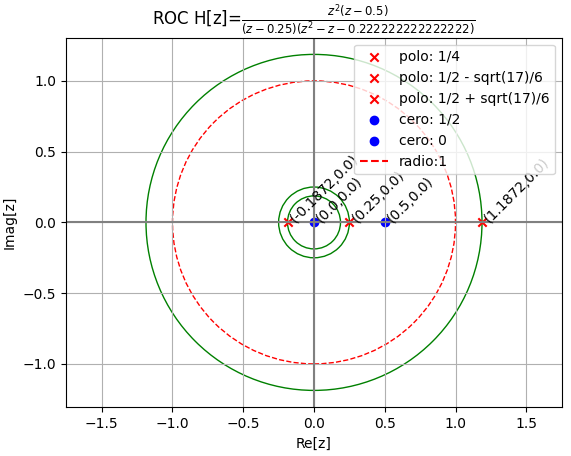
que se observa también como:
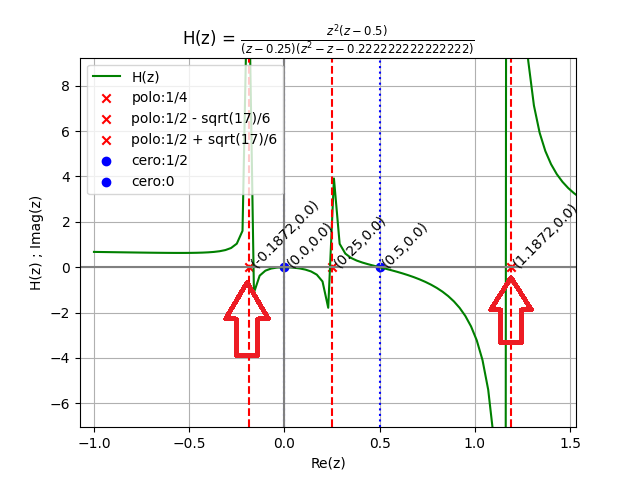
El modelo se puede plantear como:
H[z] = \frac{z^2\Big(z-\frac{1}{2}\Big)}{\Big(z-\frac{1}{4}\Big)\Big(z^2-z-\frac{2}{9}\Big)}
para usar fracciones parciales modificadas, se multiplica cada lado por 1/z:
\frac{H[z]}{z} = \frac{z\Big(z-\frac{1}{2}\Big)}{\Big(z-\frac{1}{4}\Big)\Big(z^2-z-\frac{2}{9}\Big)}
Se puede plantear un modelo de respuesta por cada raíz como:
\frac{H[z]}{z} = \frac{k1}{z-\frac{1}{4}}+\frac{k_2 z +k_3}{z^2-z-\frac{2}{9}}
usando el método de Heaviside,
k_1 = \frac{z\Big(z-\frac{1}{2}\Big)}{\cancel{\Big(z-\frac{1}{4}\Big)}\Big(z^2-z-\frac{2}{9}\Big)}\Big|_{z=\frac{1}{4}}
k_1 = \frac{\frac{1}{4}\Big(\frac{1}{4}-\frac{1}{2}\Big)}{\Big(\frac{1}{4}^2-\frac{1}{4}-\frac{2}{9}\Big)}
k_1 = -\frac{1}{16}\frac{1}{\frac{(4)(9)-(16)(9)-(2)(16)(4)}{(16)(4)(9)}} =\frac{36}{236}
con lo que ahora en la expresión se convierte en:
\frac{H[z]}{z} = \frac{z\Big(z-\frac{1}{2}\Big)}{\Big(z-\frac{1}{4}\Big)\Big(z^2-z-\frac{2}{9}\Big)} =\frac{\frac{36}{236}}{z-\frac{1}{4}}+\frac{k_2 z +K_3}{z^2-z-\frac{2}{9}} =
Usando el método de los factores cuadráticos, se multiplica ambos lados por z y z→∞
\frac{H[z]}{z} z = \frac{z^2\Big(z-\frac{1}{2}\Big)}{\Big(z-\frac{1}{4}\Big)\Big(z^2-z-\frac{2}{9}\Big)} =\frac{\frac{36}{236}z}{z-\frac{1}{4}}+z\frac{k_2 z +K_3}{z^2-z-\frac{2}{9}} =
se divide numerador y denominador del lado izquierdo para 1/z3 y el lado derecho el primer termino 1/z y el segundo termino 1/z2
\frac{\Big(1-\frac{1}{2}\frac{1}{z}\Big)}{\Big(1-\frac{1}{4}\frac{1}{z}\Big)\Big(1-\frac{1}{z}-\frac{2}{9}\frac{1}{z^2}\Big)} =\frac{\frac{36}{236}}{1-\frac{1}{4}\frac{1}{z}}+\frac{k_2 +K_3\frac{1}{z}}{1-\frac{1}{z}-\frac{2}{9}\frac{1}{z}}
y cuando z→∞
\frac{\Big(1-\frac{1}{2}(0)\Big)}{\Big(1-\frac{1}{4}(0)\Big)\Big(1-(0)-\frac{2}{9}(0)\Big)} =\frac{\frac{36}{236}}{1-\frac{1}{4}(0)}+\frac{k_2 +K_3(0)}{1-(0)-\frac{2}{9}(0)}
1 =\frac{36}{236}+k_2
k_2 = 1-\frac{36}{236}=\frac{200}{236} = \frac{50}{59}
con lo que K2=50/59 , para encontrar K3 se usa un valor conveniente de z=0
H[0] = \frac{(0)\Big((0)-\frac{1}{2}\Big)}{\Big((0)-\frac{1}{4}\Big)\Big((0)^2-(0)-\frac{2}{9}\Big)} =\frac{\frac{36}{236}}{(0)-\frac{1}{4}}+\frac{\frac{50}{59}(0) +K_3}{(0)^2-(0)-\frac{2}{9}} =
0 =\frac{\frac{36}{236}}{-\frac{1}{4}}+\frac{K_3}{-\frac{2}{9}} =
K_3 = \frac{2}{9}\frac{\frac{36}{236}}{-\frac{1}{4}} = -4\frac{2}{9}\frac{36}{236} = -\frac{8}{59}
\frac{H[z]}{z} = \frac{36}{236}\frac{1}{z-\frac{1}{4}}+\frac{50/59 z -8/59}{z^2-z-\frac{2}{9}} =
\frac{H[z]}{z} = \frac{36}{236}\frac{1}{z-\frac{1}{4}}+\frac{2}{59}\frac{25 z -4}{z^2-z-\frac{2}{9}}
y restaurando en fracciones parciales al multiplicar por z cada lado
H[z] = \frac{9}{59}\frac{z}{z-\frac{1}{4}}+\frac{2}{59}\frac{z(25 z -4)}{z^2-z-\frac{2}{9}}
los valores no se ajustan al modelo planteado en el enunciado, y existe un polo con radio>1, por lo que el sistema es creciente,y otro polo en posición r<0.
h[n] = a \alpha^n \mu [n] + b \beta^n \mu[n] + c \gamma^n \mu [n]
obtenga entonces los valores pertinentes.
| a= 9/59 = 0.1525 |
b= ... creciente sin cota, con polo mayor a 1 |
c=... con polo negativo, lo que es un término con signo alternado. |
| α= 1/4 = 0.25 |
β = 1/2 + np.sqrt(17)/6 = 1.1871842709362768 |
γ = 1/2 - np.sqrt(17)/6 = -0.18718427093627676 |
Resultados iniciales con el algoritmo
Se encuentra que hay un término que no se puede usar para encontrar la transformada z.
Hz:
2
3 z
z - --
2
-------------------
2
3 5*z z 1
z - ---- + -- + --
4 36 18
Hz en fracciones parciales
50*z*(z - 4/25) 9*z
--------------- + ------------
/ 2 2\ 59*(z - 1/4)
59*|z - z - -|
\ 9/
Hz en factores
2
z *(z - 0.5)
---------------------------------------
/ 2 \
(z - 0.25)*\z - z - 0.222222222222222/
{Q_polos:veces}: {1/4: 1, 1/2 - sqrt(17)/6: 1, 1/2 + sqrt(17)/6: 1}
{P_ceros:veces}: {1/2: 1, 0: 2}
parametros cuadraticos:
termino: 50*z*(z - 4/25)/(59*(z**2 - z - 2/9))
r : 120.72788283210394
gamma : None
beta : None
theta : None
estabilidad asintótica en z:
circ1_dentro : 2
circ1_repetidos : 0
circ1_sobre : 0
circ1_fuera : 1
unicos : 3
repetidos : 0
asintota : inestable
h[n]:
-n
9*4 *Heaviside(n)
------------------
59
revisar terminos sin transformada de tabla:
50*z*(z - 4/25)/(59*(z**2 - z - 2/9))
señal discreta h[n]
n : [0. 1. 2. 3. 4. 5. 6. 7. 8. 9.]
h[n]: [1.52542373e-01 3.81355932e-02 9.53389831e-03 2.38347458e-03
5.95868644e-04 1.48967161e-04 3.72417903e-05 9.31044756e-06
2.32761189e-06 5.81902973e-07]
Instrucciones en Python
Desarrollo con las expresiones iniciales, sin corrección sobre los parámetros que se indican en el enunciado.
Nota: cuando se produzca el siguiente error con Numpy para evaluar una expresión con exponente negativo,
Traceback (most recent call last):
File "D:\MATG1052Ejemplos\Transformadaz\ejercicio03.py", line 93, in
fi = f_n(ki)
File "", line 2, in _lambdifygenerated
return (9/59)*4**(-n)*Heaviside(n, 1/2)
ValueError: Integers to negative integer powers are not allowed.
proceda actualizando los valores a evaluar como tipo real (dtype float), tan solo usando en la línea de ki con lo siguiente:
ki = np.arange(0,muestras_fn,1.0)
quedando las instrucciones de la siguiente forma, que si evalúa valores para realizar gráficas.
# Transformada z- Fracciones parciales
# https://blog.espol.edu.ec/telg1001/lti-dt-transformada-z-xz-fracciones-parciales-con-python/
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt
import telg1001 as fcnm
#sym.SYMPY_DEBUG=True
# INGRESO
z = sym.Symbol('z')
n = sym.Symbol('n', real=True)
# coeficientes como racional en dominio 'ZZ' enteros
a0 = sym.Rational(1,2)
a1 = sym.Rational(5,4)
a2 = sym.Rational(1,36)
a3 = sym.Rational(1,18)
Pz = z**3-a0*z**2
Qz = z**3-a1*z**2+a2*z+a3
F = Pz/Qz
# para graficar
f_nombre = 'H' # nombre de función[z]: H,X,Y, etc
muestras_fn = 10 # muestras para f[n]
# PROCEDIMIENTO
Fz = fcnm.apart_z(F)
Fz_factor = sym.factor(F.evalf())
Fz_factor = fcnm._round_float_is_int(Fz_factor)
# polos y ceros de Hz
[P,Q] = F.as_numer_denom()
P = sym.poly(P,z)
Q = sym.poly(Q,z)
P_ceros = sym.roots(P)
Q_polos = sym.roots(Q)
estable_z = fcnm.estabilidad_asintotica_z(Q_polos)
# Inversa de transformada z
fn = 0*n ; f_noeval = 0*n ; Qz2_term =[]
term_sum = sym.Add.make_args(Fz)
for term_k in term_sum:
term_kn = fcnm.inverse_z_transform(term_k,z,n)
if type(term_kn)==tuple:
fn = fn + term_kn[0]
elif term_kn is not None:
fn = fn + term_kn
elif term_kn is None:
f_noeval = f_noeval + term_k
Qz2 = fcnm.Q_cuad_z_parametros(term_k)
if Qz2:
Qz2_term.append(Qz2)
fn = fn.collect(sym.Heaviside(n))
fn = fn.collect(sym.DiracDelta(n))
# SALIDA
print('\n '+f_nombre+'z:')
sym.pprint(F)
print('\n '+f_nombre+'z en fracciones parciales')
sym.pprint(Fz)
print('\n '+f_nombre+'z en factores')
sym.pprint(Fz_factor)
print('\n {Q_polos:veces}:',Q_polos)
print(' {P_ceros:veces}:',P_ceros)
if len(Qz2_term)>0:
print('\nparametros cuadraticos: ')
for i in range(0,len(Qz2_term),1):
for unterm in Qz2_term[i]:
print(' termino:',unterm)
fcnm.print_resultado_dict(Qz2_term[i][unterm])
print('\nestabilidad asintótica en z:')
fcnm.print_resultado_dict(estable_z)
print('\n '+f_nombre.lower()+'[n]:')
sym.pprint(fn)
if not f_noeval==sym.S.Zero:
print('revisar terminos sin transformada de tabla:')
print(f_noeval)
# # GRAFICA -----------
fig_ROC = fcnm.graficar_Fz_polos(Fz_factor,Q_polos,P_ceros,
muestras=101,f_nombre=f_nombre)
fig_Fz = fcnm.graficar_Fs(Fz_factor,Q_polos,P_ceros,
muestras=101,
f_nombre=f_nombre)
# graficar f[n] -------
f_n = sym.lambdify(n,fn.expand(),modules=fcnm.equivalentes)
ki = np.arange(0,muestras_fn,1.0)
fi = f_n(ki)
print('\nseñal discreta '+f_nombre.lower()+'[n]')
print('n :',ki)
print(f_nombre.lower()+'[n]:',fi)
# graficar f[n]
fig_fn, grafxn = plt.subplots()
plt.axvline(0,color='grey')
plt.stem(ki,fi)
plt.grid()
plt.xlabel('n')
plt.ylabel(f_nombre.lower()+'[n]')
etiqueta = r''+f_nombre.lower()+'[n]= $'+str(sym.latex(fn))+'$'
plt.title(etiqueta)
plt.show()