Ejercicio: 2Eva2011TI_T2 LTI DT Determinar H[z] desde bloques

literal a. expresión de la función de transferencia

El diagrama de bloques del enunciado se reordena de la siguiente forma:

El nuevo diagrama muestra que el sistema tiene dos sub-componentes en paralelo.

H[z] = -\frac{(11/2)z +7}{z^2-1z-2} +\frac{z}{2} -\frac{9}{2}

como existen varios componentes, se pueden tratar de forma separada.

H[z] = H_1[z] +\frac{z}{2} -\frac{9}{2} H_1[z] = -\frac{(11/2)z +7}{z^2-z-2}

los polos y ceros de H₁

 {Q_polos:veces}: {2: 1, -1: 1}
 {P_ceros:veces}: {-14/11: 1}

H_1[z] = -\frac{(11/2)z +7}{(z-2)(z+1)}

usando fracciones parciales modificadas

\frac{H_1[z]}{z} = -\frac{(11/2)z +7}{z(z-2)(z+1)} = \frac{k_1}{z}+\frac{k_2}{z-2}+\frac{k_3}{z+1}

usando el algoritmo se tiene:

\frac{H_1[z]}{z} = \frac{\frac{7}{2}}{z}-\frac{3}{z-2}-\frac{\frac{1}{2}}{z+1}

restaurando a fracciones parciales, al multiplicar cada lado por z, se obtiene la función de transferencia H[z] completa como componentes en paralelo junto con H₁

H_1[z] = \frac{7}{2}-\frac{3z}{z-2}-\frac{1}{2}\frac{z}{z+1}

usando la tabla de transformadas z

h_1[n] = \frac{7}{2}\delta[n]-3(2)^n \mu[n] -\frac{1}{2}(-1)^n \mu[n]

Usando el algoritmo de la sección X[z] Fracciones parciales modificadas con Python para H1[z]

con entrada:

# coeficientes como racional en dominio 'ZZ' enteros
a0 = sym.Rational(11,2)

Pz = -(a0*z+7)
Qz = z**2-z-2

se obtiene:

 Hz:
  11*z    
- ---- - 7
   2      
----------
 2        
z  - z - 2

 Hz en fracciones parciales
      z        3*z    7
- --------- - ----- + -
  2*(z + 1)   z - 2   2

 Hz en factores
-3.5*(0.785714285714286*z + 1) 
-------------------------------
      (0.5*z - 1)*(z + 1)      

 {Q_polos:veces}: {2: 1, -1: 1}
 {P_ceros:veces}: {-14/11: 1}

estabilidad asintótica en z:
circ1_dentro : 0
circ1_repetidos : 0
circ1_sobre : 1
circ1_fuera : 1
unicos : 2
repetidos : 0
asintota : inestable

 h[n]:
/      n       \                               
|  (-1)       n|                7*DiracDelta(n)
|- ----- - 3*2 |*Heaviside(n) + ---------------
\    2         /                       2       

señal discreta h[n]
n   : [0. 1. 2. 3. 4. 5. 6. 7. 8. 9.]
h[n]: [    0.     -5.5   -12.5   -23.5   -48.5
         -95.5  -192.5  -383.5  -768.5 -1535.5]

resultado que se completan con los términos de los otros componentes, al incorporar la expresión con los elementos en paralelo como se desarrolla en el siguiente literal.

Instrucciones en Python

# Transformada z- Fracciones parciales
# https://blog.espol.edu.ec/telg1001/lti-dt-transformada-z-xz-fracciones-parciales-con-python/
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt
import telg1001 as fcnm
#sym.SYMPY_DEBUG=True

# INGRESO
z = sym.Symbol('z')
n = sym.Symbol('n', real=True)

# coeficientes como racional en dominio 'ZZ' enteros
a0 = sym.Rational(11,2).limit_denominator(100)

Pz = -(a0*z+7)
Qz = z**2-z-2
F = Pz/Qz

# para graficar
f_nombre = 'H'    # nombre de función[z]: H,X,Y, etc
muestras_fn = 10  # muestras para f[n]

# PROCEDIMIENTO
Fz  = fcnm.apart_z(F)
Fz_factor = sym.factor(F.evalf())

# polos y ceros de Hz
[P,Q] = F.as_numer_denom()
P = sym.poly(P,z)
Q = sym.poly(Q,z)
P_ceros = sym.roots(P)
Q_polos = sym.roots(Q)

estable_z = fcnm.estabilidad_asintotica_z(Q_polos)

# Inversa de transformada z
fn = 0*n ; Fz_revisar = [] ; Qz2_term =[]
term_sum = sym.Add.make_args(Fz)
for term_k in term_sum:
    term_kn = fcnm.inverse_z_transform(term_k,z,n)
    if type(term_kn)==tuple:
        fn = fn + term_kn[0]
    elif term_kn is not None:
        fn = fn + term_kn
    elif term_kn is None:
        f_noeval = f_noeval + term_k
    Qz2 = fcnm.Q_cuad_z_parametros(term_k)
    if Qz2:
        Qz2_term.append(Qz2)
fn = fn.collect(sym.Heaviside(n))
fn = fn.collect(sym.DiracDelta(n))
#fn = fcnm._round_float_is_int(fn)

# SALIDA
print('\n '+f_nombre+'z:')
sym.pprint(F)
print('\n '+f_nombre+'z en fracciones parciales')
sym.pprint(Fz)
print('\n '+f_nombre+'z en factores')
sym.pprint(Fz_factor)
print('\n {Q_polos:veces}:',Q_polos)
print(' {P_ceros:veces}:',P_ceros)
if len(Qz2_term)>0:
    print('\nparametros cuadraticos: ')
    for i in range(0,len(Qz2_term),1):
        for unterm in Qz2_term[i]:
            print(' termino:',unterm)
            fcnm.print_resultado_dict(Qz2_term[i][unterm])
print('\nestabilidad asintótica en z:')
fcnm.print_resultado_dict(estable_z)
print('\n '+f_nombre.lower()+'[n]:')
sym.pprint(fn)
if len(Fz_revisar)>0:
    print('revisar terminos sin transformada de tabla:')
    for un_term in Fz_revisar:
        print(un_term)

# # GRAFICA  -----------
fig_ROC = fcnm.graficar_Fz_polos(Fz_factor,Q_polos,P_ceros,
                      muestras=101,f_nombre=f_nombre)

fig_Fz = fcnm.graficar_Fs(Fz_factor,Q_polos,P_ceros,
                     muestras=101,
                     f_nombre=f_nombre)

# graficar f[n] -------
f_n = sym.lambdify(n,fn.expand(),modules=fcnm.equivalentes)
ki  = np.arange(0,muestras_fn,1.0)
fi  = f_n(ki)

print('\nseñal discreta '+f_nombre.lower()+'[n]')
print('n   :',ki)
print(f_nombre.lower()+'[n]:',fi)

# graficar f[n]
fig_fn, grafxn = plt.subplots()
plt.axvline(0,color='grey')
plt.stem(ki,fi)
plt.grid()
plt.xlabel('n')
plt.ylabel(f_nombre.lower()+'[n]')
etiqueta = r''+f_nombre.lower()+'[n]= $'+str(sym.latex(fn))+'$'
plt.title(etiqueta)

plt.show()

literal b. Ecuación de diferencias

Se realiza la conversión por la suma de cada componente (en paralelo):

Para y₁[n]:

Y_1[z] = H_1[z]X[z] = \Big[-\frac{(11/2)z +7}{z^2-z-2}\Big] X[z] Y_1[z] [z^2-z-2]= -(11/2)zX[z] -7X[z] y_![n+2] - y_1[n+1] -2y_1[n] = -\frac{11}{2} x[n+1] -7x[n]

Para y₂[n]:

Y_2[z] = H_2[z]X[z] = \frac{z}{2}X[z] y_2[n] = \frac{1}{2}x[n+1]

Para y₃[n]:

Y_3[z] = H_3[z]X[z] = -\frac{9}{2} X[z] y_3[n] = -\frac{9}{2} x[n]

se suman las expresiones obtenidas de Y₁[z] + Y₂[z]+Y₃[z]

y[n+2] - y[n+1] -\cancel{2y[n]} +\cancel{y[n]} + \cancel{y[n]}= -\frac{11}{2} x[n+1] -7x[n] +\frac{1}{2}x[n+1]-\frac{9}{2} x[n]

la ecuación de diferencias simplificada es;

y[n+2] - y[n+1] = -5 x[n+1] -\frac{23}{2} x[n]

El sistema global se puede reescribir nuevamente en z como

z^2Y[z] - zY[z] = -5 zX[z] -\frac{23}{2} X[z] z(z-1)Y[z] = (-5 z -\frac{23}{2}) X[z]

se tiene que el sistema tienen polos en 0 y 1, que se encuentran dentro del radio 1 del plano z.

literal d. Respuesta al impulso H[z]

H[z] se obtiene a partir de la última ecuación

H[z] = \frac{Y[z]}{H[z]} = -\frac{5 z +\frac{23}{2}}{z(z-1)}

aplicando fracciones parciales modificadas:

\frac{H[z]}{z} = -\frac{5 z +\frac{23}{2}}{z^2(z-1)} \frac{H[z]}{z} = \frac{33}{2} \frac{1}{z} +\frac{23}{2}\frac{1}{z^2} -\frac{33}{2} \frac{1}{z-1}

restaurando fracciones parciales al multiplicar por z

H[z] = \frac{33}{2} +\frac{23}{2} \frac{1}{z} -\frac{33}{2} \frac{z}{z-1}

usando la tabla de transformada z se tiene:

h[n] = \frac{33}{2}\delta [n] +\frac{23}{2} \delta [n-1] - \frac{33}{2} \mu[n]

usando el algoritmo con entrada:

# coeficientes como racional en dominio 'ZZ' enteros
a0 = sym.Rational(11,2)
a1 = sym.Rational(9,2)
a2 = sym.Rational(23,2)
#F = -(a0*z+7)/(z**2-z-2) + z/2 -a1
F = -(5*z+a2)/(z*(z-1))

se tiene como resultado:

 Hz:
-5*z - 23/2
-----------
 z*(z - 1) 

 Hz en fracciones parciales
  16.5*z          11.5
- ------ + 16.5 + ----
  z - 1            z  

 Hz en factores
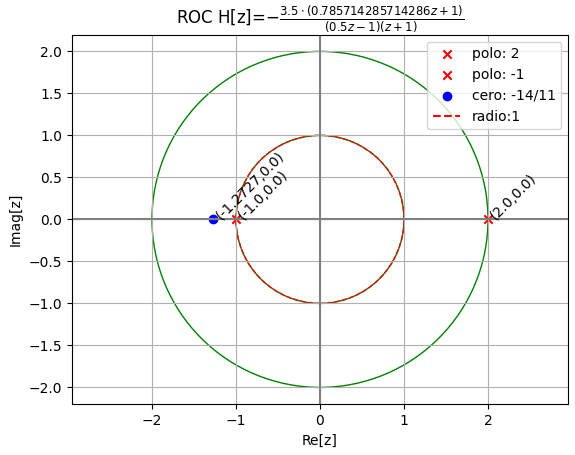
-11.5*(0.434782608695652*z + 1) 
--------------------------------
           z*(z - 1)            

 {Q_polos:veces}: {1: 1, 0: 1}
 {P_ceros:veces}: {-2.30000000000000: 1}

estabilidad asintótica en z:
circ1_dentro : 1   circ1_repetidos : 0 
circ1_sobre : 1  circ1_fuera : 0
unicos : 2  repetidos : 0
asintota : marginalmente estable

 h[n]:
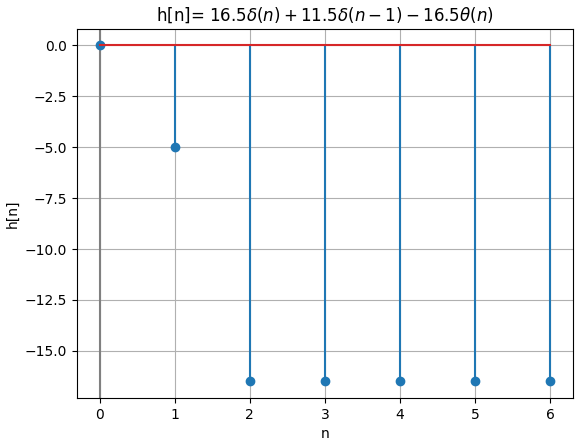
16.5*DiracDelta(n) + 11.5*DiracDelta(n - 1) - 16.5*Heaviside(n)

señal discreta h[n]
n   : [0. 1. 2. 3. 4. 5. 6.]
h[n]: [  0.   -5.  -16.5 -16.5 -16.5 -16.5 -16.5]