Categoría: 3ra Evaluación

3ra Evaluación I Término 2010-2011. 16/Septiembre/2010. TELG1001

Tema3. (20 puntos) De acuerdo a la figura que se muestra a continuació, a un sistema LTI-CT cuya función de transferencia

H(s) = e^{\frac{\pi}{6}s}

le ingresa una señal

x(t) = x₁(t) – x₂(t) + x₃(t)

a. Determine y esquematice el espectro de magnitud y fase de las series de Fourier complejas y exponenciales de x(t).

b. Determine y esquematice el espectro de magnitud y fase de las series de Fourier complejas y exponenciales de y(t).

c. Determine la potencia de la señal de salida y(t).

---

Coordinador: Tama Alberto

3ra Evaluación I Término 2010-2011. 16/Septiembre/2010. TELG1001

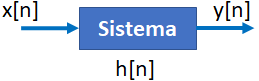
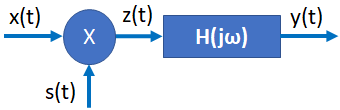
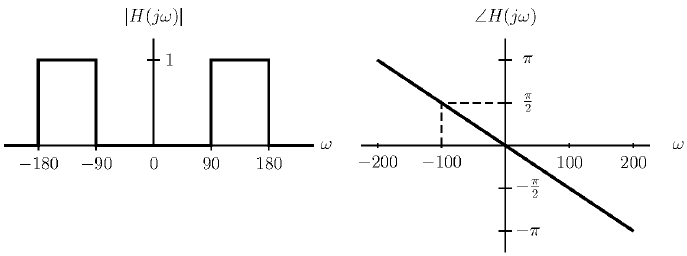
Tema2. (20 puntos) Un estudiante de la materia Sistemas Lineales, ha determinado que la respuesta impulso h(t) de un sistema LTI-CT, es aquella que se muestra en la siguiente figura.

Si el referido sistema es excitado con la señal cuadrada periódica x(t),

determinar, esquematizar y etiquetar según corresponda:

a. La respuesta de frecuencia H(ω) vs ω.

b. La respuesta de frecuencia X(ω) vs ω.

c. La respuesta de frecuencia Y(ω) vs ω y Z(ω) vs ω.

d. La expresión analítica de la salida y(t).

---

Coordinador: Tama Alberto

 

3ra Evaluación II Término 2009-2010. 18/Febrero/2010. TELG1001

Tema 3. (20 puntos) Para el sistema mostrado en la figura, determinar:

a. La Transformada de Fourier de las señales x₁(t) y x₂(t), es decir X₁(ω) y X₂(ω), esquematizando el respectivo espectro de Fourier.

b. La transformada de Fourier de la señal z(t), es decir Z(ω), esquematizando el respectivo espectro de Fourier para cuando a=1 y ω₀=2.

c. La transformada de Fourier de la señal y(t), es decir Y(ω), esquematizando su espectro de magnitud y fase para cuando a=1 y ω₀=2.

3ra Evaluación II Término 2009-2010. 18/Febrero/2010. TELG1001

Tema 1. (20 puntos) Una señal de entrada sinusoidal x(t) = cos(10t) es muestreada y filtrada tal como se aprecia en la siguiente figura:

Donde la respuesta de frecuencia del filtro está dada por:

|H(j \omega)| = \begin {cases} 1 , 90 <|\omega|<180 \\ 0, \text{en otro caso}\end{cases} \angle H(j \omega) = - \frac{\pi \omega}{200}

a. Suponiendo que

s(t) = \sum_{k=-\infty}^{\infty} \delta(t-kT) T= \frac{2 \pi}{90}

Determinar, esquematizar y etiquetar la Transformada de Fourier de la señal z(t). Es decir Z(jω).

b. Determinar la respuesta del sistema, es decir, y(t)