Referencia: Lathi 2.4-1 p170, Ej 2.8 p173.
El integral de convolución de dos funciones x(t) y h(t) usa como operador el símbolo ⊗ que representa el integral de la ecuación mostrada.
La función h(t) representa la repuesta del sistema, función de transferencia o respuesta a impulso, que por la forma de obtenerla se considera causal por tener componente μ(t) y δ(t) que aseguraría que la función se desarrolle en el lado derecho del plano.
x(t) \circledast h(t) = \int_{-\infty}^{+\infty} x(\tau)h(t-\tau) \delta \tauLa función x(t) representa la entrada del sistema y el integral de convolución se utiliza para determinar la respuesta de estado cero de un sistema ZSR.
Si las funciones x(t) y el sistema h(t) son causales, la respuesta también será causal. Teniendo como límites del integral τa = 0 y τb = t
y(t)=\begin{cases}\int_{0^{-}}^{t} x(\tau)h(t-\tau) \delta \tau , & t\ge 0\\ 0, & t<0 \end{cases}El límite inferior del integral se usa como 0-, implica aunque se escriba solo 0 se pretende evitar la dificultad cuando x(t) tiene un impulso en el origen.
Convolución: [ ejemplo 1: x(t) y h(t) causales ] [ ejemplo 2 : x(t) no causal y h(t) causal ] [ejemplo 3: rectangulo y rampa]
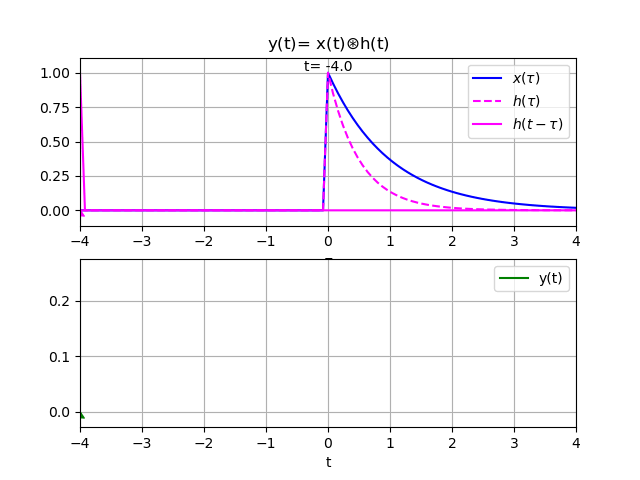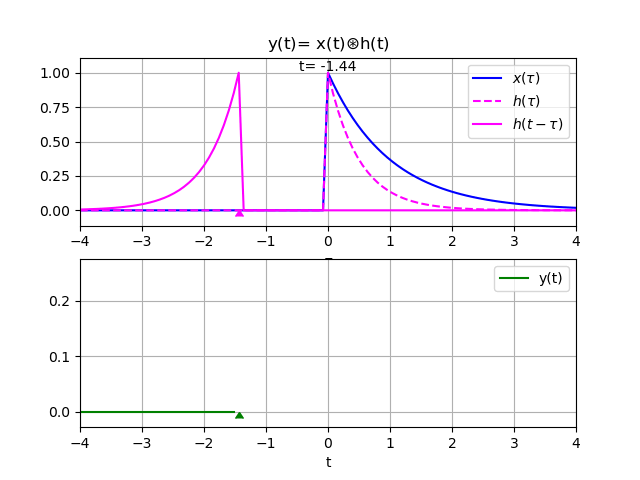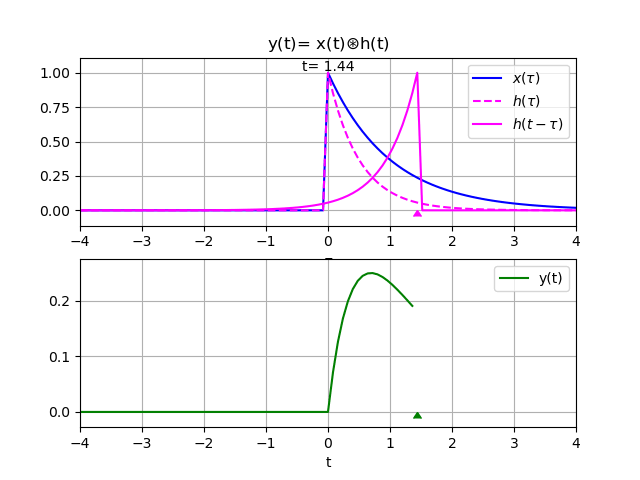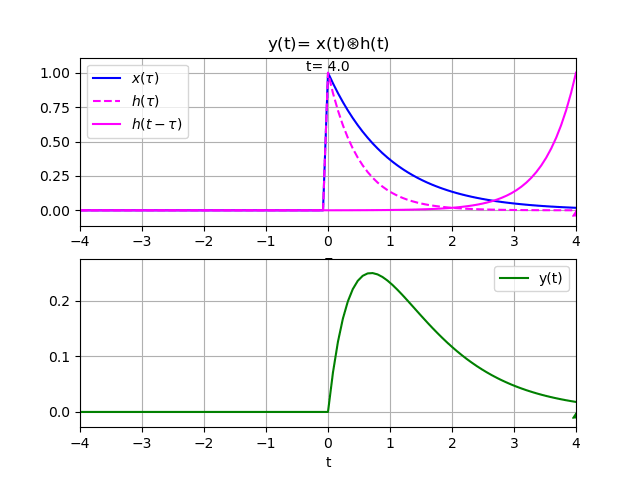
Ejemplo 1. Algoritmo para el integral de convolución con x(t) y h(t) causales con Sympy
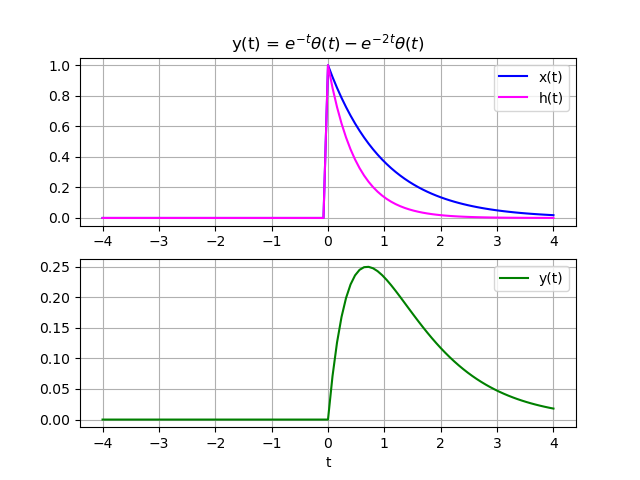
Realizar la convolución entre la respuesta al impulso h(t) y la entrada x(t) mostradas:
x(t) = e^{-t} \mu(t) h(t) = e^{-2t} \mu(t)Para el algoritmo, se define las variables a usar, escalón e impulso unitarios, definiendo las funciones x(t) y y(t) como:
# entrada x(t), respuesta impulso h(t)
x = sym.exp(-t)*u
h = sym.exp(-2*t)*u
Se revisa la causalidad de las señales para actualizar los límites del integral de convolución.
xcausal = fcnm.es_causal(x) hcausal = fcnm.es_causal(h) # limites de integral de convolución tau_a = -sym.oo ; tau_b = sym.oo if hcausal==True: tau_b = t if (xcausal and hcausal)==True: tau_a = 0
El integral de convolución se aplica a la multiplicación entre x(t) y h(t), realizando el cambio de variable por τ y (t-τ). Para facilitar la operación del integral, se simplifica la expresión xh como términos de suma
# integral de convolucion xh = x.subs(t,tau)*h.subs(t,t-tau) xh = sym.expand(xh,t) y = sym.integrate(xh,(tau,tau_a,tau_b)) y = sym.expand(y,t) y = y.subs(u**2,u) # Heaviside**2=Heaviside
El resultado del integral se muestra como,
xcausal: True hcausal: True limites de integral: [ 0 , t ] x(t)*h(t-tau): -2*t tau e *e *Heaviside(tau)*Heaviside(t - tau) y(t): -t -2*t e *Heaviside(t) - e *Heaviside(t)
Instrucciones en Python
# Integral de convolucion con Sympy # Revisar causalidad de x(t) y h(t) import numpy as np import matplotlib.pyplot as plt import sympy as sym equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] import telg1001 as fcnm # INGRESO t = sym.Symbol('t',real=True) tau = sym.Symbol('tau',real=True) u = sym.Heaviside(t) d = sym.DiracDelta(t) # entrada x(t), respuesta impulso h(t) x = sym.exp(-t)*u h = sym.exp(-2*t)*u # grafica intervalo [t_a,t_b] simetrico a 0 t_b = 4 ; t_a = -t_b muestras = 201 # PROCEDIMIENTO xcausal = fcnm.es_causal(x) hcausal = fcnm.es_causal(h) # limites de integral de convolución tau_a = -sym.oo ; tau_b = sym.oo if hcausal==True: tau_b = t if (xcausal and hcausal)==True: tau_a = 0 # integral de convolucion x(t)*h(t) xh = x.subs(t,tau)*h.subs(t,t-tau) xh = sym.expand(xh,t) y = sym.integrate(xh,(tau,tau_a,tau_b)) y = sym.expand(y,t) if not(y.has(sym.Integral)): y = fcnm.simplifica_escalon(y) #ZSR = ZSR.subs(u**2,u) # Heaviside**2=Heaviside # SALIDA print('xcausal: ',xcausal) print('hcausal: ',hcausal) print('limites de integral: [',tau_a,',',tau_b,']') print('x(t)*h(t-tau):') sym.pprint(xh) print('\n y(t):') sym.pprint(y) if hcausal==False: print('revisar causalidad de h(t)') if xcausal==False: print('revisar causalidad de x(t)')
Grafica para el integral de convolución entre x(t) y h(t)
Con los resultados se puede construir la gráfica, para observar en un intervalo simétrico que permita visualizar la operación de convolución.
Instrucciones complementarias para las gráficas, se realiza como una función a ser añadida a telg1001.py por ser reutilizada en los ejercicios.
# GRAFICA ----- def graficar_xh_y(xt,ht,yt,t_a,t_b, muestras=101,x_nombre='x', h_nombre='h',y_nombre='y'): '''dos subgraficas, x(t) y h(t) en superior h(t) nn inferior ''' # grafica evaluacion numerica x_t = sym.lambdify(t,xt,modules=equivalentes) h_t = sym.lambdify(t,ht,modules=equivalentes) ti = np.linspace(t_a,t_b,muestras) xi = x_t(ti) hi = h_t(ti) y_t = sym.lambdify(t,yt,modules=equivalentes) yi = y_t(ti) colorlinea_y = 'green' if y_nombre =='ZSR': colorlinea_y = 'dodgerblue' fig_xh_y, graf2 = plt.subplots(2,1) untitulo = y_nombre+'(t) = $'+ str(sym.latex(yt))+'$' graf2[0].set_title(untitulo) graf2[0].plot(ti,xi, color='blue', label='x(t)') graf2[0].plot(ti,hi, color='magenta', label='h(t)') graf2[0].legend() graf2[0].grid() graf2[1].plot(ti,yi,colorlinea_y, label = y_nombre+'(t)') graf2[1].set_xlabel('t') graf2[1].legend() graf2[1].grid() #plt.show() return(fig_xh_y) figura_xh_y = graficar_xh_y(x,h,y,t_a,t_b,muestras) plt.show()
Convolución: [ ejemplo 1: x(t) y h(t) causales ] [ ejemplo 2 : x(t) no causal y h(t) causal ] [ejemplo 3: rectángulo y rampa]
Ejercicio 2. Convolución entre h(t) causal y x(t) no causal
Referencia: Opennheim 2.8 p101
Realizar la convolución entre h(t) y x(t) mostradas:
x(t) = e^{2t} \mu (-t) h(t) = \mu (t-3)La señal x(t) es creciente desde el lado izquierdo del plano, es decir es no causal, también es acotada en cero por el escalón unitario invertido en el tiempo.
Mientras que h(t) presenta una respuesta con retraso de 3 unidades de tiempo con el escalón unitario, se encuentra en el lado derecho del plano, por lo que se la considera causal.
Para el análisis, el gráfico se presenta la animación de la operación de convolución
Para el ejercicio, es importante considerar que en un sistema lineal causal, solo se desarrolla una salida y(t) ante una entrada x(t). La señal de entrada x(t) no se registra a partir de tiempo con valor cero. Observe en la gráfica que la señal de salida y(t) se desarrolla con retardo de tres unidades respecto a la entrada.
Desde luego el sistema responderá en cualquier momento que se presenta la señal, por lo que x(t) podría ser no causal, La referencia de t=0 se considera desde el punto de vista del sistema h(t).
# entrada x(t), respuesta impulso h(t) x = sym.exp(-2*t)*u h = u # grafica intervalo [t_a,t_b] plano simétrico t_b = 5 ; t_a = -t_b muestras = int(t_b)*10+1
Esto implica que de darse el caso que exista un h(t) no causal y x(t) causal, por la propiedad conmutativa de la convolución, para el desarrollo del integral se pueden intercambiar las entradas y hacerlo mas simple.
# intercambia si h(t) no es_causal # con x(t) es_causal por propiedad conmutativa intercambia = False if hcausal==False and xcausal==True: temporal = h h = x x = temporal xcausal = False hcausal = True intercambia = True
El resultado con el algoritmo es:
xcausal: False hcausal: True limites de integral: [ -oo , t ] x(t)*h(t-tau): 2*tau e *Heaviside(-tau)*Heaviside(t - tau - 3) ZSR(t): / -6 2*t \ |e *e 1| 1 |-------- - -|*Heaviside(3 - t) + - \ 2 2/ 2 revisar causalidad de x(t)
En la respuesta se observa que el témino u(3-t)/2 en -∞ se convierte en 1/2 que anula la constante de 1/2 del tercer término. Al revisar la convergencia del primer término se encuentra que tiende a cero, en consecuencia en la señal hacia el lado izquierdo tiende a cero.
gráfica con el algoritmo
Instrucciones en Python
Para los ejercicios se agrupan las instrucciones en una función respuesta_ZSR(x,h) que recibe las dos señales x(t) y h(t), como se desarrolla en la siguiente sección. En la función se analiza con los algoritmos anteriores si son de tipo causal incluida en telg1001.py.
# Integral de convolucion con Sympy # como Respuesta a estado cero ZSR con x(t) y h(t) # https://blog.espol.edu.ec/telg1001/lti-ct-respuesta-a-estado-cero-con-sympy-python/ import numpy as np import matplotlib.pyplot as plt import sympy as sym equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] import telg1001 as fcnm # INGRESO t = sym.Symbol('t',real=True) tau = sym.Symbol('tau',real=True) u = sym.Heaviside(t) d = sym.DiracDelta(t) # entrada x(t), respuesta impulso h(t) x = sym.exp(2*t)*u.subs(t,-t) h = u.subs(t,t-3) # grafica intervalo [t_a,t_b] plano simétrico t_b = 7 ; t_a = -t_b muestras = int(t_b)*10+1 # PROCEDIMIENTO # revisa causalidad de señales xcausal = fcnm.es_causal(x) hcausal = fcnm.es_causal(h) # intercambia si h(t) no es_causal # con x(t) es_causal por propiedad conmutativa intercambia = False if hcausal==False and xcausal==True: temporal = h h = x x = temporal xcausal = False hcausal = True intercambia = True # limites de integral de convolución tau_a = -sym.oo ; tau_b = sym.oo if hcausal==True: tau_b = t if (xcausal and hcausal)==True: tau_a = 0 # integral de convolución x(t)*h(t) xh = x.subs(t,tau)*h.subs(t,t-tau) xh = sym.expand(xh,t) ZSR = sym.integrate(xh,(tau,tau_a,tau_b)) ZSR = sym.expand(ZSR,t) if not(ZSR.has(sym.Integral)): ZSR = fcnm.simplifica_escalon(ZSR) #ZSR = ZSR.subs(u**2,u) # Heaviside**2=Heaviside lista_escalon = ZSR.atoms(sym.Heaviside) ZSR = sym.expand(ZSR,t) # terminos suma ZSR = sym.collect(ZSR,lista_escalon) # restaura si hubo intercambio de x(t) y h(t) if intercambia == True: xcausal = True hcausal = False # graficar si no tiene Integral o error cond_graf = not(ZSR.has(sym.Integral)) cond_graf = cond_graf and not(ZSR.has(sym.oo)) cond_graf = cond_graf and not(ZSR.has(sym.nan)) # SALIDA print('xcausal: ',xcausal) print('hcausal: ',hcausal) print('limites de integral: [',tau_a,',',tau_b,']') print('x(t)*h(t-tau):') if xh.is_Add: i=0 for term_suma in xh.args: if i>0: print('+') sym.pprint(term_suma) i=i+1 else: sym.pprint(xh) print('\n ZSR(t):') sym.pprint(ZSR) if hcausal==False: print('revisar causalidad de h(t)') if xcausal==False: print('revisar causalidad de x(t)') if intercambia: print('considere intercambiar h(t)con x(t)') if not(cond_graf): print('revisar acortar x(t) o h(t) para BIBO') # GRAFICA if cond_graf: figura_xh_y = fcnm.graficar_xh_y(x,h,ZSR,t_a,t_b, muestras,y_nombre='ZSR') else: # terminos de integrales sin evaluar, infinito o nan figura_x = fcnm.graficar_ft(x,t_a,t_b,muestras,'x') figura_h = fcnm.graficar_ft(h,t_a,t_b,muestras,'h') #plt.show() # grafica animada de convolución # n_archivo = '' # sin crear archivo gif animado n_archivo = 'convolucion02' # requiere 'imagemagick' if cond_graf: figura_animada = fcnm.graf_animada_xh_y(x,h,ZSR,t_a,t_b, muestras, reprod_x = 4,y_nombre='y', archivo_nombre = n_archivo) plt.show()
Convolución: [ ejemplo 1: x(t) y h(t) causales ] [ ejemplo 2 : x(t) no causal y h(t) causal ] [ejemplo 3: rectangulo y rampa]
Ejemplo 3. Convolución entre rectangular y rampa causales
Referencia: Oppenheim Ejemplo 2.7 p99
Realizar la convolución entre las siguientes dos señales:
x(t) = \mu (t) - \mu (t-1) h(t) = t\mu (t) - t\mu (t-2)Para el desarrollo analítico, se propone considerar usar las funciones por intervalos separados:
y(t) = \begin{cases} 0 , & t \lt 0 \\ \frac{1}{2} t^2 , & 0 \lt t \lt T \\ Tt-\frac{1}{2}T^2 , & T \lt t \lt 2T \\ - \frac{1}{2}t^2 + Tt + \frac{3}{2} T^2 , & 2T \lt t \lt 3T \\ 0 . & 3T \lt t \end{cases}Con las indicaciones se propone como tarea realizar el desarrollo analítico. Observando la gráfica animada y considerando los intervalos propuestos.

El resultado con el algoritmo del ejercicio anterior es:
xcausal: True
hcausal: True
limites de integral: [ 0 , t ]
x(t)*h(t-tau):
t*Heaviside(tau)*Heaviside(t - tau)
+
t*Heaviside(tau - 1)*Heaviside(t - tau - 2)
+
tau*Heaviside(tau)*Heaviside(t - tau - 2)
+
tau*Heaviside(t - tau)*Heaviside(tau - 1)
+
-t*Heaviside(tau)*Heaviside(t - tau - 2)
+
-t*Heaviside(t - tau)*Heaviside(tau - 1)
+
-tau*Heaviside(tau)*Heaviside(t - tau)
+
-tau*Heaviside(tau - 1)*Heaviside(t - tau - 2)
ZSR(t):
2 2
t *Heaviside(t)*Heaviside(t - 1) t *Heaviside(t)
- -------------------------------- + --------------- +
2 2
2 2 2
t *Heaviside(t - 3)*Heaviside(t - 2) t *Heaviside(t - 2)
+ ------------------------------------ - -------------------- +
2 2
+ t*Heaviside(t)*Heaviside(t - 1) - t*Heaviside(t - 3)*Heaviside(t - 2)
Heaviside(t)*Heaviside(t - 1) 3*Heaviside(t- 3)*Heaviside(t - 2)
- ----------------------------- - ----------------------------------- +
2 2
2
+ 2*Heaviside(t - 2)
>>>
En el resultado del algoritmo se encuentra que es necesario simplificar la expresión resultante al menos para los términos con escalón unitario, tales como u*u o u*u(t-1). Sympy '1.11.1' aún no incorpora esta simplificación, por lo que se realiza una función que revise término a término la expresión.
La función para simplificar escalón unitario multiplicados se desarrolla en Simplificar multiplicación entre impulso δ(t) o escalón unitario μ(t) con Sympy
De donde se obtiene la instrucción para el algoritmo,
ZSR = fcnm.simplifica_escalon(ZSR)
El resultado luego de aplicar la función sobre ZSR se muestra un poco mas simple:
ZSR(t):
2 2 2 2
t *Heaviside(t) t *Heaviside(t - 3) t *Heaviside(t - 2) t *Heaviside(t - 1)
--------------- + ------------------- - ------------------- - -------------------
2 2 2 2
3*Heaviside(t - 3) Heaviside(t - 1)
- t*Heaviside(t - 3) + t*Heaviside(t - 1) - ------------------ - ----------------
2 2
+ 2*Heaviside(t - 2)
y si reagrupan las expresiones por cada escalón desplazado con sym.collect() se puede obtener:
lista_escalon = ZSR.atoms(sym.Heaviside)
ZSR = sym.expand(ZSR,t) # terminos suma
ZSR = sym.collect(ZSR,lista_escalon)
con el siguiente resultado:
ZSR(t):
2 / 2\ / 2 \
t *Heaviside(t) | t | | t 1|
--------------- + |2 - --|*Heaviside(t - 2) + |- -- + t - -|*Heaviside(t - 1)
2 \ 2 / \ 2 2/
/ 2 \
|t 3|
+ |-- - t - -|*Heaviside(t - 3)
\2 2/
Convolución: [ ejemplo 1: x(t) y h(t) causales ] [ ejemplo 2 : x(t) no causal y h(t) causal ] [ejemplo 3: rectangulo y rampa]
Refererencia: But what is a convolution? 3Blue1Brown. 18 nov 2022
Referencia: Convolutions | Why X+Y in probability is a beautiful mess. 3Blue1Brown. 27-Junio-2023.