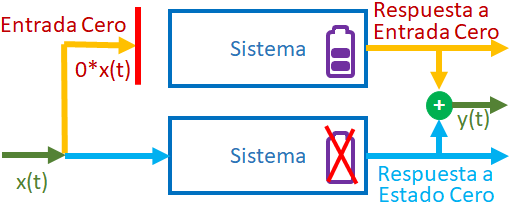
La respuesta total del sistema integra las respuestas obtenidas para entrada cero y estado cero. Se resume el desarrollo de un ejercicio con todos los componentes para el ejemplo 1 Modelo entrada-salida para circuitos RLC realizada con Sympy-Python y las funciones del curso en telg1001.py.
| Respuesta total |
= | respuesta a entrada cero |
+ | respuesta a estado cero |
| ZSR = h(t) ⊗ x(t) |
Referencia: Lathi 1.8-1 p111. Oppenheim problema 2.61c p164 Ejemplo 9.24 p700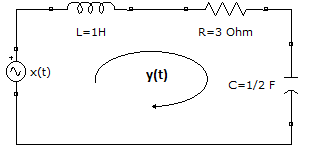
Para el ejemplo, se plantea determinar la corriente de lazo y(t) del circuito mostrado en la imagen.
\frac{dy(t)}{dt} +3 y(t) + 2\int_{-\infty}^t y(\tau)d\tau = x(t)Como se había indicado en los desarrollos preliminares, para tener todo expresado con un solo operador, se derivan ambos lados de la ecuación:
\frac{d^{2}y(t)}{dt^{2}} + 3\frac{dy(t)}{dt} + 2y(t) = \frac{dx(t)}{dt}En la entrada de sistema se aplica:
x(t) = 10 e^{-3t} \mu (t)Para la respuesta se considera que la respuesta total del sistema se puede describir en forma gráfica como el resultado de dos componentes:
Se plantea el ejercicio para encontrar la respuesta a entrada cero ZIR y la respuesta a estado cero ZSR
Es de considerar que para las gráficas de las respuestas se considera que el sistema es observable, aplicable, usable desde t=0, dado que la solución para entrada cero no se ha acotado en los resultados. Imagine sistema con un capacitor entre sus componentes que a la salida que se descarga desde un voltaje de 1 voltio desde t=0, esta situación no necesariamente implica que podríamos conocer si viene descargandose desde 1.5, 3, 9, 12, o 1000 voltios. Observación a considerar con en la interpretación de los ejercicios para valores obtenidos antes de t=0 que es el punto inicial de observacion.
Resultados con el Algoritmo en Sympy-Python
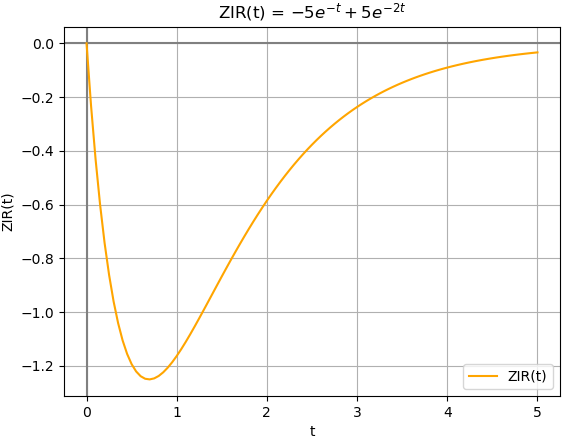
ZIR(t):
-t -2*t
- 5*e + 5*e
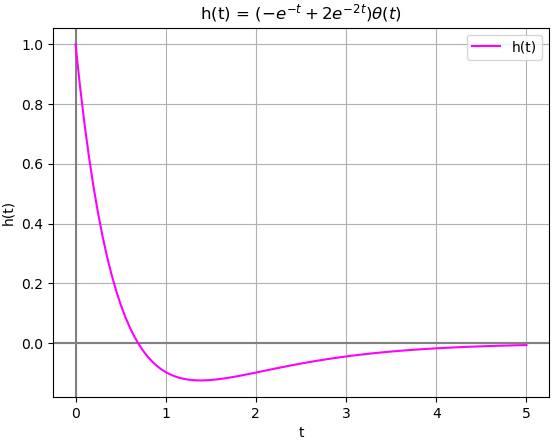
h(t):
/ -t -2*t\
\- e + 2*e /*Heaviside(t)
ZSR(t):
-t -2*t -3*t
- 5*e *Heaviside(t) + 20*e *Heaviside(t) - 15*e *Heaviside(t)
xcausal: True
hcausal: True
limites de integral: [ 0 , t ]
y(t) = ZIR(t)+ZSR(t):
-t -t -2*t -2*t -3*t
- 5*e *Heaviside(t) - 5*e + 20*e *Heaviside(t) + 5*e - 15*e *Heaviside(t)
>>>
Graficas de y(t) = ZIR(t)+ZSR(t)
Instrucciones en Python
# Respuesta total del sistema # y(t) = ZIR(t) + ZSR(t) # https://blog.espol.edu.ec/telg1001/lti-ct-yszirzsr-respuesta-del-sistema-con-sympy-python/ # Revisar causalidad de x(t) y h(t) import numpy as np import matplotlib.pyplot as plt import sympy as sym equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] import telg1001 as fcnm # INGRESO t = sym.Symbol('t',real=True) tau = sym.Symbol('tau',real=True) y = sym.Function('y') x = sym.Function('x') h = sym.Function('h') u = sym.Heaviside(t) # ecuacion: lado izquierdo = lado derecho # Left Hand Side = Right Hand Side LHS = sym.diff(y(t),t,2) + 3*sym.diff(y(t),t,1) + 2*y(t) RHS = sym.diff(x(t),t,1,evaluate=False) ecuacion = sym.Eq(LHS,RHS) # condiciones iniciales [y'(t0),y(t0)] t0 = 0 cond_inicio = [-5,0] # entrada x(t) x = 10*sym.exp(-3*t)*u # grafica intervalo [t_a,t_b] t_a = 0; t_b = 5 muestras = 201 # PROCEDIMIENTO # Respuesta entrada cero ZIR sol_ZIR = fcnm.respuesta_ZIR(ecuacion,cond_inicio,t0) ZIR = sol_ZIR['ZIR'] # Respuesta al impulso h(t) sol_h = fcnm.respuesta_impulso_h(ecuacion) h = sol_h['h'] # respuesta a estado cero ZSR sol_ZSR = fcnm.respuesta_ZSR(x,h) ZSR = sol_ZSR['ZSR'] xh = sol_ZSR['xh'] # respuesta a y(t) = ZIR(t)+ZSR(t) y_total = ZIR+ZSR # revisa si grafica ZSR if not(sol_ZSR['cond_graf']): print('revisar acortar x(t) o h(t) para BIBO') # SALIDA print('\n ZIR(t):') sym.pprint(ZIR) print('\n h(t):') sym.pprint(h) print('\n ZSR(t):') sym.pprint(ZSR) print('xcausal: ',sol_ZSR['xcausal']) print('hcausal: ',sol_ZSR['hcausal']) print('limites de integral:', sol_ZSR['[tau_a,tau_b]']) print('\n y(t) = ZIR(t)+ZSR(t):') sym.pprint(y_total) # GRAFICA figura_ZIR = fcnm.graficar_ft(ZIR,t_a,t_b, muestras,'ZIR') figura_h = fcnm.graficar_ft(h,t_a,t_b, muestras,'h') # grafica animada de convolución n_archivo = '' # sin crear archivo gif animado # n_archivo = 'LTIC_YTotal_ZIR_Ej01' # requiere 'imagemagick' if sol_ZSR['cond_graf']: fig_ZSR = fcnm.graficar_xh_y(x,h,ZSR,t_a,t_b, muestras,y_nombre='ZSR') fig_ytotal = fcnm.graficar_xhy(ZIR,ZSR,y_total,t_a,t_b, muestras,x_nombre='ZIR', h_nombre='ZSR',y_nombre='y') figura_animada = fcnm.graf_animada_xh_y(x,h,ZSR,-t_b,t_b, muestras, reprod_x = 4,y_nombre='ZSR', archivo_nombre = n_archivo) plt.show()
El algoritmo en Sympy incorpora los pasos realizados con el desarrollo analítico de solución a ecuaciones diferenciales lineales.
Existen otros métodos como el de Transformada de Laplace que simplifica el paso de realizar el integral de convolución, pues al cambiar al dominio 's' en lugar de tiempo las operaciones son mayoritariamete sobre polinomios. La siguiente unidad desarrolla el tema.