Referencia: Lathi 3.8 p282, Oppenheim 2.1.2 p77 pdf108, Hsu 2.6.C p62
Una señal discreta de entrada x[n] se representa como una superposición de versiones escaladas de un conjunto de impulsos unitarios desplazados δ[n-k], cada uno con valor diferente de cero en un solo punto en el tiempo, especificado por el valor de k.
La respuesta de un sistema lineal y[n] a x[n] es la superposición de las respuestas escaladas del sistema a cada uno de estos impulsos desplazados.
Si usamos hk[n] como la respuesta del sistema lineal al impulso unitario desplazado por δ[n-k]. La respuesta y[n] del sistema lineal a la entrada x[n] en la ecuación será la combinación lineal ponderada de las respuesta básicas.
y[n] = \sum_{k=-\infty}^{+\infty} x[k]h_{k}[n]Si se conoce la respuesta de un sistema lineal al conjunto de impulsos unitarios desplazados, podemos construir una respuesta a una entrada arbitraria.
Si el sistema lineal también es invariante en el tiempo, entonces estas respuestas a impulsos unitarios desplazados en el tiempo son todas las versiones desplazadas en el tiempo unas de otras.
h[n] es la salida del sistema LTI cuando δ[n] es la entrada. Entonces para un sistema LTI la ecuación se vuelve.
y[n] = \sum_{k=-\infty}^{+\infty} x[k]h[n-k]El resultado se conoce como la "convolución de suma" o "suma de superposición" y la operación miembro derecho de la ecuación se llama convolución de las secuencias x[n] y h[n] que se representa de manera simbólica como:
y[n] = x[n]*h[n]Ejemplo
Referencia: Openheim Ejemplo 2.4 p85 pdf116
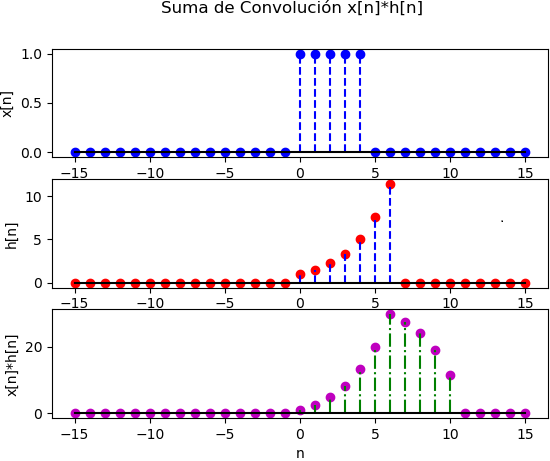
Considere una entrada x[n] y una respuesta al impulso unitario h[n] dada por:
x[n] = (u[n]-u[n-5])
h[n] = αn (u[n]-u[n-7])
con α>1. Para el ejercicio, α=1.5.
Nota: Para el algoritmo, si α es un entero, por ejemplo 2, usar α=2.0, para que la operación potencia se realice con números reales, como entero se puede saturar y dar error.
Al aplicar la suma de convolución obtiene:
Para aplicar el algoritmo se requiere definir u[n], por ser parte de las funciones x[n] y h[n]. Dado que la operación requiere valores fuera del rango muestreado para n, la sección suma convolución utiliza las funciones en lugar de los vectores xi, hi.
La función está definida en un intervalo simétrico, por lo que el rango de trabajo [a,b] se mantiene de la forma [-b,b] en las instrucciones.
# Respuesta a impulsos - forma discreta # Ejemplo Oppenheim Ejemplo 2.3 p83/pdf111 import numpy as np import matplotlib.pyplot as plt # INGRESO # Rango [a,b], simétrico a 0 b = 15 ; a = -b alfa = 1.5 u = lambda n: np.piecewise(n,n>=0,[1,0]) x = lambda n: u(n)-u(n-5) h = lambda n: (alfa**n)*(u(n)-u(n-7)) # PROCEDIMIENTO ni = np.arange(a,b+1,1) xi = x(ni) hi = h(ni) # Suma de Convolucion x[n]*h[n] muestras = len(xi) yi = np.zeros(muestras, dtype=float) for i in range(0,muestras): suma = 0 for k in range(0,muestras): suma = suma + x(ni[k])*h(ni[i]-ni[k]) yi[i] = suma # yi = np.convolve(xi,hi,'same') # SALIDA - GRAFICA plt.figure(1) plt.suptitle('Suma de Convolución x[n]*h[n]') plt.subplot(311) plt.stem(ni,xi, linefmt='b--', markerfmt='bo',basefmt='k-') plt.ylabel('x[n]') plt.subplot(312) plt.stem(ni,hi, linefmt='b--', markerfmt='ro',basefmt='k-') plt.ylabel('h[n]') plt.subplot(313) plt.stem(ni,yi, linefmt='g-.', markerfmt='mo', basefmt='k-') plt.ylabel('x[n]*h[n]') plt.xlabel('n') plt.show()
La suma convolución se encuentra también disponible con Numpy en np.convolve(), la sección de suma convolución se puede reemplazar y obtener los mismos resultados. Considere que para éste caso se usan los vectores xi y hi.
yi = np.convolve(xi,hi,'same')
el algoritmo se puede aplicar a otros ejercicios para comprobar los resultados.
Continúe con el ejercicio 2.5 del libro.