6.3.1 LTI DT – Respuesta impulso h[n]. Ejercicio con Python

Referencia: Lathi Ejemplo 3.17, 3.18  y 3.19 p277-278

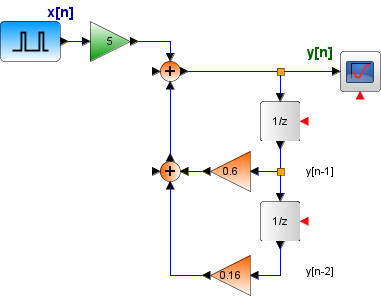
Determine la respuesta al impulso unitario de un sistema LTID descrito por la ecuación de diferencias mostrada,

$y[n+2] - 0.6 y[n+1] - 0.16 y[n] = 5x[n+2]$

---

Para el diagrama se usa la ecuación desplazada en dos unidades,

$y[n] - 0.6 y[n-1] - 0.16 y[n-2] = 5x[n]$ $y[n] = 0.6 y[n-1] + 0.16 y[n-2] + 5x[n]$

En la entrada se usa un impulso unitario x[n] = δ[n]

Desarrollo Analítico

Se requieren al menos dos valores iniciales en el ejercicio, por lo que se emplea la ecuación en forma iterativa, recordando que x[n] = δ[n], siendo entonces y[n] = h[n]

$y[n] - 0.6 y[n-1] - 0.16 y[n-2] = 5x[n]$ $h[n] - 0.6 h[n-1] - 0.16 h[n-2] = 5\delta [n]$

aplicando para n=0

$h[0] - 0.6 h[-1] - 0.16 h[-2] = 5\delta[0]$ $h[0] - 0.6 (0) - 0.16 (0) = 5(1)$ $h[0] = 5$

luego se aplica para n = 1

$h[1] - 0.6 h[0] - 0.16 h[-1] = 5 \delta[1]$ $h[1] - 0.6 (5) - 0.16 (0) = 5(0)$ $h[1] = 3$

El ejercicio es continuación del primer ejercicio de respuesta a entrada cero, por lo que simplificamos el desarrollo como

$(E^2 - 0.6 E - 0.16) y[n] = 5 E^2 x[n]$ $\gamma^2 - 0.6 \gamma - 0.16 = 0$

con raíces características γ₁=-0.2 y γ₂=0.8,

con los modos característicos se tiene que

$y_c[n] = c_1 (-0.2)^n + c_2 (0.8)^n$

que se convierte a:

$h[n] = [c_1 (-0.2)^n + c_2 (0.8)^n ] \mu [n]$

Para determinar c₁ y c₂ se recurre a encontrar dos valores de forma iterativa, con n=0 y n=1.

$h[0] = [c_1 (-0.2)^0 + c_2 (0.8)^0 ] \mu [0]$ $h[0] = c_1 + c_2$ $h[1] = [c_1 (-0.2)^1 + c_2 (0.8)^1 ] \mu [1]$ $h[1] = -0.2 c_1 + 0.8 c_2$

los valores de h[0]=5 y h[1]=3 se encontraron de forma iterativa

$5 = c_1 + c_2$ $3 = -0.2 c_1 + 0.8 c_2$

resolviendo con Python:

>>> import numpy as np
>>> A = [[ 1., 1.],
         [-0.2, 0.8]]
>>> B = [5.,3.]
>>> np.linalg.solve(A,B)
array([1., 4.])
>>> 

encontrando que c₁=1 y c₂=4

teniendo como resultado final:

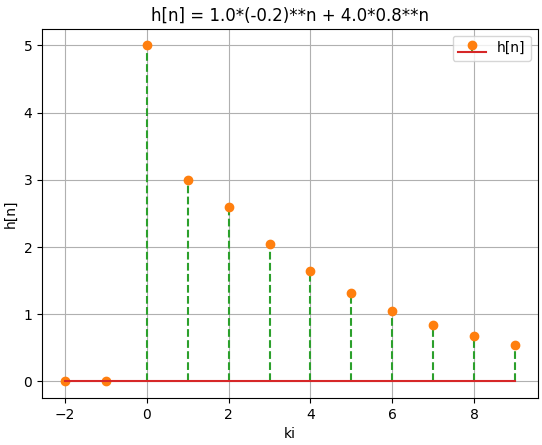
$h[n] = [ (-0.2)^n +4 (0.8)^n ] \mu [n]$

---

Algoritmo en Python

La respuesta para el procedimiento anterior realizada con Python es:

 respuesta impulso: 
hi: [5. 3.]
Matriz: 
[[ 1.   1. ]
 [ 0.8 -0.2]]
Ch:  [4. 1.]
n>=0, hn:  
        n          n
1.0*-0.2  + 4.0*0.8 
>>>

se desarrolla el algoritmo a partir de entrada cero, continuando con el cálculo iterativo de h[n] para los valores iniciales, luego determina los valores de los coeficientes de la ecuación h[n]

# Sistema LTID. Respuesta impulso
# QE con raices Reales NO repetidas Lathi ejemplo 3.13 pdf271
# Lathi ejemplo 3.18 y 3.19 pdf278,
# blog.espol.edu.ec/telg1001
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt

# INGRESO
# coeficientes E con grado descendente
QE = [1., -0.6, -0.16]
PE = [5.,  0,    0   ]
# condiciones iniciales ascendente ...,y[-2],y[-1]
inicial = [25/4, 0.]

tolera = 1e-6  # casi_cero
muestras = 10  # para grafica

# PROCEDIMIENTO
# Respuesta a ENTRADA CERO
# raices, revisa numeros complejos
gamma = np.roots(QE)
revisaImag = np.iscomplex(gamma)
escomplejo = np.sum(revisaImag)

# coeficientes de ecuacion
m_q = len(QE)-1
Ac = np.zeros(shape=(m_q,m_q),dtype=float)

# revisa si parte compleja <tolera o casi_cero 
if escomplejo>0:
    for i in range(0,m_q,1):
        valorimag = np.imag(gamma[i])
        if np.abs(valorimag)<tolera:
            gamma[i] = float(np.real(gamma[i]))
    sumaj = np.sum(np.abs(np.imag(gamma)))
    if sumaj <tolera:
        print(sumaj)
        gamma = np.real(gamma)
        escomplejo = 0

# revisa repetidos
unicoscuenta = np.unique(gamma,return_counts=True)
repetidas = np.sum(unicoscuenta[1]-1)

# Respuesta impulso h[n]
ki = np.arange(-m_q,m_q,1)
hi = np.zeros(m_q, dtype=float)
xi = np.zeros(2*m_q, dtype=float)
xi[m_q] = 1 # impulso en n=0
Ah = np.zeros(shape=(m_q,m_q),dtype=float)

# h[n] iterativo
p_n = len(PE)
for i in range(0,m_q,1):
    for k in range(m_q,2*m_q,1):
        hi[i] = hi[i] - QE[k-m_q]*hi[m_q-k+1]
    for k in range(0,p_n,1):
        hi[i] = hi[i] + PE[k]*xi[m_q+i]
Bh = np.copy(hi[:m_q])

# coeficientes de ecuacion
for i in range(0,m_q,1):
    for j in range(0,m_q,1):
        Ah[i,j] = gamma[j]**(i)
ch = np.linalg.solve(Ah,Bh)

# ecuacion hn
n = sym.Symbol('n')
hn = 0*n
for i in range(0,m_q,1):
    hn = hn + ch[i]*(gamma[i]**n)

# SALIDA
if escomplejo == 0: 
    print('\n respuesta impulso: ')
    print('Bh:',Bh)
    print('Matriz: ')
    print(Ah)
    print('Ch: ',ch)
    print('n>=0, hn:  ')
    sym.pprint(hn)
else:
    print(' existen raices con números complejos.')
    print(' usar algoritmo de la sección correspondiente.')
    

# grafica datos
ki = np.arange(-m_q,muestras,1)
hi = np.zeros(muestras+m_q)

if escomplejo == 0: 
    # evaluación de h[n]
    h_n = sym.lambdify(n,hn)
    hi[m_q:] = h_n(ki[m_q:])

    # grafica h[n]
    plt.stem(ki,hi,label='h[n]',
             markerfmt ='C1o',
             linefmt='C2--')
    plt.legend()
    plt.grid()
    plt.ylabel('h[n]')
    plt.xlabel('ki')
    plt.title('h[n] = '+str(hn))
    plt.show()

Comentario: Aunque es relativamente simple determinar la respuesta al impulso h[n] usando el método descrito, el desarrollo del tema se realiza mejor en la unidad con Transformada z. Lathi p280.