Publicado en por Edison Del Rosario

s1Eva2010TII_T1 LTI CT Determinar h(t) con entrada x(t) y salida y(t)

Ejercicio: 1Eva2010TII_T1 LTI CT Determinar h(t) con entrada x(t) y salida y(t)

Dadas las señales de entrada y salida del sistema:

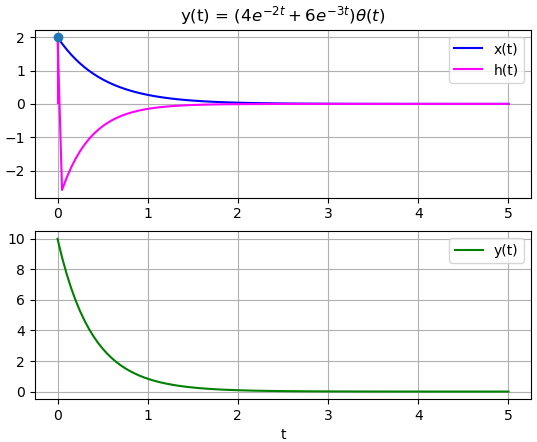
y(t) = \Big( 4 e^{-2t} + 6 e^{-3t} \Big) \mu (t) x(t) = 2 e^{-2t} \mu (t)

literal a. h(t)

Se usan las transformadas de Laplace para plantear la respuesta al impulso como  H(s) = Y(s)/X(s)

Y(s) = 4 \frac{1}{s+2} + 6 \frac{1}{s+3} = \frac{4(s+3)+6(s+2)}{(s+2)(s+3)} Y(s) = \frac{4s+12+6s+12}{(s+2)(s+3)} =\frac{10s+24}{(s+2)(s+3)} X(s) = 2 \frac{1}{s+2}

se obtiene la expresión para H(s),

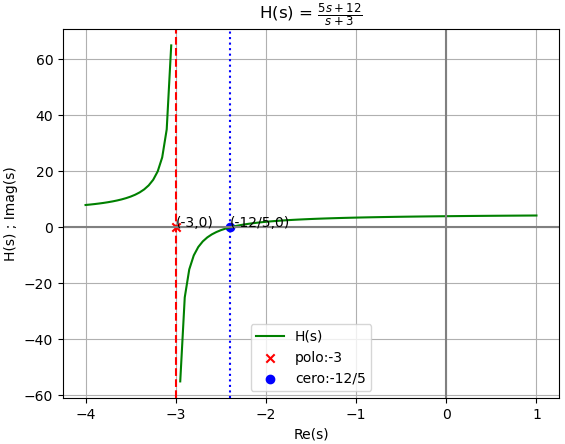
H(s) = \frac{Y(s)}{H(s)} = \frac{\frac{10s+24}{(s+2)(s+3)}}{2 \frac{1}{s+2}} = \frac{2(5s+12)(s+2)}{2(s+2)(s+3)} H(s) = \frac{5s+12}{s+3}

aplicando fracciones parciales, conociendo que el grado M del polinomio P es igual al grado N del polinomio Q, existe un término constante mas terminos cero(k)/(s+polo(k)). El término constante es el coeficiente de s de mayor grado del numerador.

H(s) = 5-\frac{3}{s+3}

Aplicando la Transformada Inversa de Laplace, se tiene:

h(t) = 5\delta(t)-3e^{-3t} \mu (t)

con lo que comparando el resultado con la ecuación sugerida, a= 5, b=-3, c =3.

literal b. ecuación diferencial de h(t)

tomando la forma:

H(s) = \frac{5s+12}{s+3} \frac{Y(s)}{X(s)} = \frac{5s+12}{s+3} (s+3)Y(s) = (5s+12)X(s) sY(s)+3Y(s) = 5sX(s)+12X(s) \frac{\delta}{\delta t}y(t)+3y(t) = 5\frac{\delta}{\delta t}x(t)+12x(t)

Literal c. Diagrama de bloques

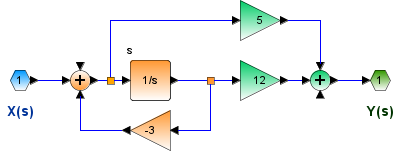Literal d. polos

El sistema tiene un polo en -3 , que se encuentra en el lado izquierdo del plano s, lo que indica que tiene términos decrecientes y es asintóticamente estable. Lo mismo aplica para el caso de BIBO estable.

Tarea. literal e.

Para la señal indicada, considere revisar la propiedad de diferenciación en la tabla de propiedades transformada de Laplace.

\frac{\delta}{\delta t} x(t) \rightarrow sX(s) -x(0\text{–})

Resultados con Python

 y(t)
/   -2*t      -3*t\             
\4*e     + 6*e    /*Heaviside(t)
Y(s)
  6       4  
----- + -----
s + 3   s + 2

 x(t)
   -2*t             
2*e    *Heaviside(t)
X(s)
  2  
-----
s + 2

H(s) = P(s)/Q(s):
      3  
5 - -----
    s + 3

H(s) en factores:
5*s + 12
--------
 s + 3  

 h(t) :
                     -3*t             
5*DiracDelta(t) - 3*e    *Heaviside(t)

polosceros:
Q_polos : {-3: 1}
P_ceros : {-12/5: 1}

Estabilidad de H(s):
 n_polos_real : 1
 n_polos_imag : 0
 enRHP : 0
 unicos : 0
 repetidos : 0
 asintota : estable

gráfica de H(s) con polos

s1Eva2010TII_T1_polos H(s)

gráfica de x(t),y(t), h(t)

s1Eva2010TII_T1_xh_y

Instrucciones en Python

# 1Eva2010TII_T1 LTI CT Determinar h(t) con entrada x(t) y salida y(t)
# Transformadas de Laplace, funciones
# https://blog.espol.edu.ec/telg1001/
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
import telg1001 as fcnm

# INGRESO
s = sym.Symbol('s')
t = sym.Symbol('t', real=True)
d = sym.DiracDelta(t)
u = sym.Heaviside(t)

yt = (4*sym.exp(-2*t)+6*sym.exp(-3*t))*u

xt = 2*sym.exp(-2*t)*u

# Grafica, intervalo tiempo [t_a,t_b]
t_a = 0 ; t_b = 5
muestras = 101  # 51 resolucion grafica

# PROCEDIMIENTO
Ys = fcnm.laplace_transform_suma(yt)
Xs = fcnm.laplace_transform_suma(xt)

# H(s) respuesta a estado cero
Hs = Ys/Xs
Hs = fcnm.apart_s(Hs)
Hs_fc = fcnm.factor_exp(Hs) # en factores
Hs_Qs2 = fcnm.Q_cuad_s_parametros(Hs_fc)

polosceros  = fcnm.busca_polosceros(Hs)
Q_polos = polosceros['Q_polos']
P_ceros = polosceros['P_ceros']

estable = fcnm.estabilidad_asintotica_s(Q_polos)

ht = 0*s
term_suma = sym.Add.make_args(Hs)
for term_k in term_suma:
    ht_k = sym.inverse_laplace_transform(term_k,s,t)
    # simplifica log(exp()) ej: e**(-2s)/(s**2)
    if ht_k.has(sym.log):
        ht_k = sym.simplify(ht_k,inverse=True)
    ht  = ht + ht_k
lista_escalon = ht.atoms(sym.Heaviside)
ht = sym.expand(ht,t) # terminos suma
ht = sym.collect(ht,lista_escalon)

# SALIDA
print(' y(t)')
sym.pprint(yt)
print('Y(s)')
sym.pprint(Ys)
print('\n x(t)')
sym.pprint(xt)
print('X(s)')
sym.pprint(Xs)
print('\nH(s) = P(s)/Q(s):')
sym.pprint(Hs)
print('\nH(s) en factores:')
sym.pprint(Hs_fc)
if len(Hs_Qs2)>0:
    print('\nH(s) parámetros cuadraticos:')
    fcnm.print_resultado_dict(Hs_Qs2)

print('\n h(t) :')
sym.pprint(ht)

print('\npolosceros:')
fcnm.print_resultado_dict(polosceros)

print('\nEstabilidad de H(s):')
for k in estable:
    print('',k,':',estable[k])

# Graficas polos, H(s), con polos h(t) --------
muestras_H = 101
figura_s  = fcnm.graficar_Fs(Hs_fc,Q_polos,P_ceros,f_nombre='H',solopolos=True)
figura_Hs = fcnm.graficar_Fs(Hs_fc,Q_polos,P_ceros,muestras=muestras_H,f_nombre='H')
figura_ht = fcnm.graficar_ft(ht,t_a,t_b,muestras,f_nombre='h')
# GRAFICAS y(t),x(t),h(t) ---------------------
figura_ft = fcnm.graficar_xh_y(xt,ht,yt,t_a,t_b,muestras)
plt.show()