s1Eva2016TII_T1 LTI CT Sistema en paralelo-serie

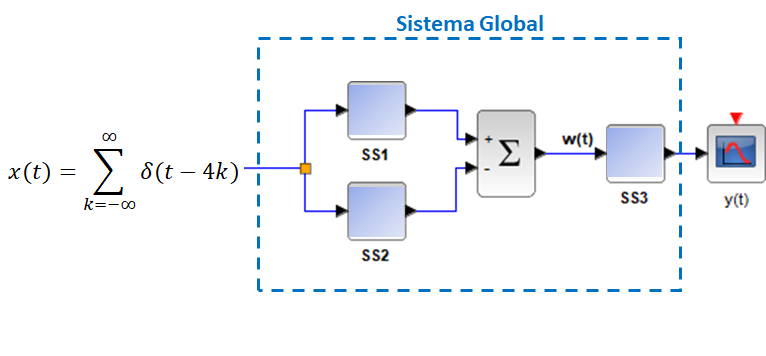
Ejercicio: 1Eva2016TII_T1 LTI CT Sistema en paralelo-serie

a. respuestas impulso de los subsistemas SS1, SS2 y SS3

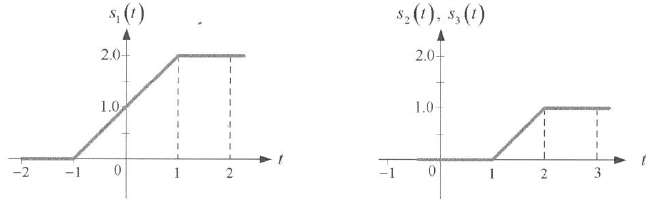
realizadas a partir de las respuestas de paso, x(t) = μ(t), entrada escalón unitario:

$s_1(t) = r(t+1) - r(t-1)$ $s_2(t) = s_3(t) = r(t-1) - r(t-2)$

---

$h_1 (t) = \frac{\delta}{\delta t} s_1(t)$ $h_1 (t) = \frac{\delta}{\delta t} [ r(t+1) - r(t-1)]$ $= \frac{\delta}{\delta t}[(t+1)\mu (t+1) - (t-1)\mu (t-1)]$ $= (1) \mu (t+1) +(t+1) \delta(t+1) -[ (1)\mu (t-1) + (t-1)\delta(t-1)]$ $= \mu (t+1) +0 -[ (1)\mu (t-1) + 0]$ $= \mu (t+1) - \mu (t-1)$

---

$h_2 (t) = \frac{\delta}{\delta t} s_2(t)$ $h_2 (t) = \frac{\delta}{\delta t} [(t-1) \mu (t-1) - (t-2) \mu (t-2)$

siguiendo el desarrollo para h₁(t)

$h_2 (t) = \mu (t-1) - \mu (t-2)$

por lo que también:

$h_3 (t) = h_2 (t) =\mu (t-1) - \mu (t-2)$

respuesta con el algoritmo:

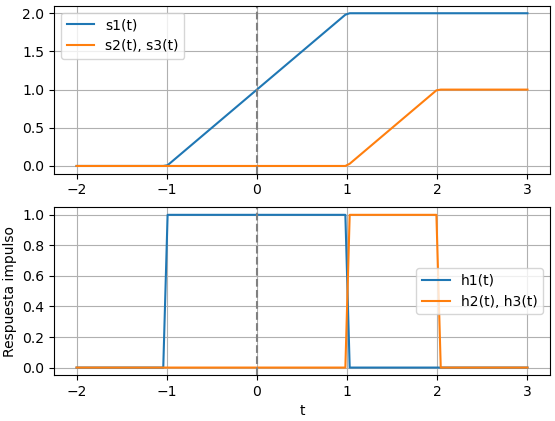
 literal a: Respuestas de paso
s1:  -(t - 1)*Heaviside(t - 1) + (t + 1)*Heaviside(t + 1)
s2:  -(t - 2)*Heaviside(t - 2) + (t - 1)*Heaviside(t - 1)
s3:  -(t - 2)*Heaviside(t - 2) + (t - 1)*Heaviside(t - 1)
 literal a: Respuestas impulso
h1:  -(t - 1)*DiracDelta(t - 1) + (t + 1)*DiracDelta(t + 1)
     - Heaviside(t - 1) + Heaviside(t + 1)
h2:  -(t - 2)*DiracDelta(t - 2) + (t - 1)*DiracDelta(t - 1)
     - Heaviside(t - 2) + Heaviside(t - 1)
h3:  -(t - 2)*DiracDelta(t - 2) + (t - 1)*DiracDelta(t - 1)
     - Heaviside(t - 2) + Heaviside(t - 1)

Instrucciones en Python

# 1Eva2016TII_T1 Sistema LTIC en paralelo-serie
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
equivalentes = [{'DiracDelta': lambda x: 1*(x==0)},
                {'Heaviside': lambda x,y: np.heaviside(x, 1)},
                'numpy',]
# INGRESO
t = sym.Symbol('t', real=True)
u = sym.Heaviside(t) 
r = t*u

# literal a, repuesta de paso
s1 = r.subs(t,t+1) - r.subs(t,t-1)
s2 = r.subs(t,t-1) - r.subs(t,t-2)
s3 = r.subs(t,t-1) - r.subs(t,t-2)

t_a = -2 ; t_b = 3

# PROCEDIMIENTO
muestras = (t_b-t_a)*(20+1)
ti = np.linspace(t_a,t_b,muestras)
s1n = sym.lambdify(t,s1, modules=equivalentes)
s2n = sym.lambdify(t,s2, modules=equivalentes)
s1i = s1n(ti)
s2i = s2n(ti)

# literal a, respuesta impulso
h1 = sym.diff(s1,t,1)
h2 = sym.diff(s2,t,1)
h3 = sym.diff(s3,t,1)

h1n = sym.lambdify(t,h1, modules=equivalentes)
h2n = sym.lambdify(t,h2, modules=equivalentes)
h3n = sym.lambdify(t,h3, modules=equivalentes)
h1i = h1n(ti)
h2i = h2n(ti)
h3i = h3n(ti)

# SALIDA
print(' literal a: Respuestas de paso')
print('s1: ',s1)
print('s2: ',s2)
print('s3: ',s3)
print(' literal a: Respuestas impulso')
print('h1: ',h1)
print('h2: ',h2)
print('h3: ',h3)

# Gráfica
plt.subplot(211)
plt.plot(ti,s1i,label ='s1(t)')
plt.plot(ti,s2i,label ='s2(t), s3(t)')
plt.axvline(0, linestyle='dashed',color='grey')
plt.legend()
plt.grid()

plt.subplot(212)
plt.plot(ti,h1i,label ='h1(t)')
plt.plot(ti,h2i,label ='h2(t), h3(t)')
plt.axvline(0, linestyle='dashed',color='grey')
plt.ylabel('Respuesta impulso')
plt.xlabel('t')
plt.legend()
plt.grid()
plt.show()

---

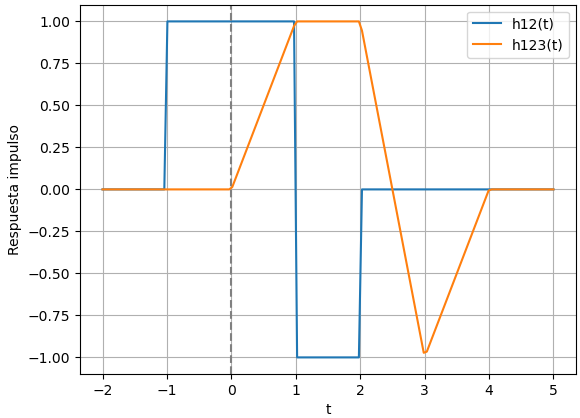
b. respuestas impulso h₁₂(t) y respuesta de paso (escalón unitario) s₁₂(t)

los sistemas SS1 y SS2 se encuentran con un operador suma en paralelo ,restando SS2, por lo que las respuestas al impulso son:

$h_{12} (t) = h_1 (t) - h_2 (t)$ $= [\mu (t+1) - \mu (t-1)] - [\mu (t-1) - \mu (t-2)]$ $= \mu (t+1) - 2 \mu (t-1) + \mu (t-2)$

la «respuesta de paso» se encuentran como:

$s_{12} (t) = \int_{-\infty}^{\infty} h_{12}(t) \delta t = h_{12} (t) \circledast \mu (t)$ $s_{12} (t) = [\mu (t+1) - 2 \mu (t-1) - \mu (t-2)] \circledast \mu (t)$

Usando la tabla de integrales de convolución, fila 3:

$s_{12} (t) = r(t+1) -2 r(t-1) + r(t-2)$

---

c. respuesta impulso del sistema global  h₁₂₃(t)

A partir de h₁₂(t) y h₃(t), que se encuentran en serie (cascada), se tiene que:

$h_{123} (t) = h_{12} (t) \circledast h_3 (t)$ $\frac{\delta}{\delta t}h_{123} (t) = \frac{\delta}{\delta t}[h_{12} (t) \circledast h_3 (t)]$ $= \frac{\delta}{\delta t}h_{12} (t) \circledast h_3 (t) = h_{12} (t) \circledast \frac{\delta}{\delta t}h_3 (t)$

usando la primera expresión equivalente de la convolución:

$\frac{\delta}{\delta t}h_{12} (t) = \frac{\delta}{\delta t}[\mu (t+1) - 2 \mu (t-1) + \mu (t-2)]$ $= \delta (t+1) - 2 \delta (t-1) + \delta (t-2)$

por lo que

$\frac{\delta}{\delta t}h_{123} (t) = [\delta (t+1) - 2 \delta (t-1) + \delta (t-2)] \circledast h_3 (t)$ $= \delta (t+1) \circledast h_3 (t) - 2 \delta (t-1) \circledast h_3 (t) + \delta (t-2) \circledast h_3 (t)$

Usando la tabla de integrales de convolución, fila 1:

$= h_3 (t+1) - 2 h_3 (t-1) + h_3 (t-2)$

y sustituyendo las expresiones con los deplazamientos en t,

$= [\mu ((t+1)-1) - \mu ((t+1)-2)]$ $-2[\mu ((t-1)-1) - \mu ((t-1)-2)]$ $+ [\mu ((t-2)-1) - \mu ((t-2)-2)]$

realizado las operaciones en los paréntesis,

$= \mu (t) - \mu (t-1)$ $- 2\mu (t-2) + 2\mu (t-3)$ $+ \mu (t-3) - \mu (t-4)$

uniendo términos iguales, se simplifica,

$\frac{\delta}{\delta t} h_{123} (t) = \mu (t) - \mu (t-1)- 2\mu (t-2) + 3\mu (t-3) - \mu (t-4)$

ahora se puede calcular h₁₂₃(t) como

$h_{123} (t) =\frac{\delta}{\delta t} h_{123} (t) \circledast \mu (t)$ $= [\mu (t) - \mu (t-1)- 2\mu (t-2) + 3\mu (t-3) - \mu (t-4)] \circledast \mu (t)$ $= \mu (t)\circledast \mu (t) - \mu (t-1)\circledast \mu (t) -2\mu (t-2)\circledast \mu (t)+$ $+ 3\mu (t-3)\circledast \mu (t) - \mu (t-4) \circledast \mu (t)$

Usando la tabla de integral de convolución, fila 3:

$h_{123} (t) = r(t) - r(t-1) -2 r(t-2)+ 3 r(t-3) - r(t-4)$

también se puede escribir en función de μ(t)

$h_{123} (t) = t \mu(t) - (t-1) \mu (t-1) -2 (t-2) \mu(t-2)+$ $+3 (t-3) \mu(t-3) - (t-4)\mu(t-4)$

Con lo que se que se obtiene la gráfica de las funciones requeridas en el literal b.

el resultado del algoritmo es:

literal b. h123(t)
h12:  (t - 2)*DiracDelta(t - 2) - 2*(t - 1)*DiracDelta(t - 1)
    + (t + 1)*DiracDelta(t + 1) + Heaviside(t - 2)
    - 2*Heaviside(t - 1) + Heaviside(t + 1)
h123:  t*Heaviside(t) - (t - 4)*Heaviside(t - 4) 
     + 3*(t - 3)*Heaviside(t - 3) -2*(t - 2)*Heaviside(t - 2)
     - (t - 1)*Heaviside(t - 1)

las instrucciones adicionales en Python son:

t_a = -2 ; t_b = 5
# PROCEDIMIENTO
muestras = (t_b-t_a)*(20+1)
ti = np.linspace(t_a,t_b,muestras)

# b. respuesta impulso y paso del sistema 12 en paralelo
h12  = h1 - h2
h12n = sym.lambdify(t,h12, modules=equivalentes)
h12i = h12n(ti)

# respuesta impulso global sistema 123
h123  = r-r.subs(t,t-1)-2*r.subs(t,t-2)
h123  = h123 + 3*r.subs(t,t-3)-r.subs(t,t-4)
h123n = sym.lambdify(t,h123, modules=equivalentes)
h123i = h123n(ti)

# SALIDA
print('\nliteral b. h123(t)')
print('h12: ', h12)
print('h123: ',h123)

# Grafica
plt.plot(ti,h12i,label ='h12(t)')
plt.axvline(0, linestyle='dashed'
            ,color='grey')
plt.plot(ti,h123i,label ='h123(t)')
plt.ylabel('Respuesta impulso')
plt.xlabel('t')
plt.legend()
plt.grid()

plt.show()

---

litera b. Tabla de respuestas

Subsistema LTIC SS1

• h₁(t) no tiene la forma kδ(T), por lo que SSI es con memoria.
• h₁(t) ≠ 0, t<0, el sistema no es causal.
• La respuesta al impulso es absolutamente integrable, por lo que es BIBO estable

Subsistema LTIC SS2 y SS3

• h₂(t) y h₂(t) no tienen la forma kδ(T), por lo que SS2 y SS3 tienen memoria.
• h₂(t) = h₃(t) = 0, t<0, los sistemas SS2 y SS3 son causales.
• La respuesta al impulso es absolutamente integrable, por lo que SS2 y SS3 son BIBO estables

Subsistema LTIC en paralelo SS1-SS2

• h₁₂(t) no tiene la forma kδ(T), por lo que SS1-SS2 en paralelo es con memoria.
• h₁₂(t) ≠ 0 t<0, el sistema en paralelo SS1-SS2 no es causal.
• La respuesta al impulso es absolutamente integrable, por lo que el sistema en paralelo SS1-SS2 es BIBO estable

Subsistema LTIC global SS1-SS2-SS3

• h₁₂₃(t) no tiene la forma kδ(T), por lo que el sistema global es con memoria.
• h₁₂(t) = 0 t<0, el sistema global es causal.
• La respuesta al impulso es absolutamente integrable, por lo que el sistema global es BIBO estable
  

  ---

  literal d. salida w(t)

La combinación en paralelo del sistema SS1 y SS2 a partir de la entrada x(t) dada es:

$w(t) = x(t) \circledast h_{12} (t) = h_{12} (t) \circledast x(t)$ $w(t) = h_{12} (t) \circledast \sum_{k=-\infty}^{\infty} \delta (t-4k)$ $= \sum_{k=-\infty}^{\infty} [h_{12} (t) \circledast\delta (t-4k)]$ $= \sum_{k=-\infty}^{\infty} h_{12} (t-4k)$

que es una función periódica con T_k = 4.

Por ser una señal periódica, la potencia y energía se determinan en un periodo:

$E_{w(t)} = \int_{-1}^{3} |w(t)|^2 \delta t$ $= \int_{-1}^{1} |1|^2 \delta t + \int_{1}^{2} |-1|^2 \delta t + \int_{2}^{3} |0|^2 \delta t$ $= \int_{-1}^{1} (1) \delta t + \int_{1}^{2} (1) \delta t = t \bigg|_{-1}^{1} + t \bigg|_{1}^{2} =2+1 =3$ $E_{w(t)} = 3$ $P_{w(t)} = \frac{E_{w(t)}}{T_0} = \frac{3}{4}$

---

literal e. salida y(t) sistema global

$y(t) = x(t) \circledast h_{123} (t) = h_{123} (t) \circledast x(t)$ $= h_{123} (t) \circledast \sum_{k=-\infty}^{\infty} \delta (t-4k)$ $= \sum_{k=-\infty}^{\infty} [h_{123} (t) \circledast \delta (t-4k)]$ $y(t) = \sum_{k=-\infty}^{\infty} h_{123}(t-4k)$

siendo una respuesta de tipo periódica con T₀ = 4, por lo que la potencia y energía se determinan en un periodo,

$E_{y(t)} = \int_{0}^{4} |y(t)|^2 \delta t$ $= \int_{0}^{1} |t|^2 \delta t + \int_{1}^{2} |1|^2 \delta t +\int_{2}^{3} |5-2t|^2 \delta t + \int_{3}^{4} |t-4|^2 \delta t$ $= \frac{t^3}{3} \Big|_0^1 + t\Big|_1^2 + \int_{2}^{3}(25-20t+4t^2) \delta t+ \int_{3}^{4} |t^2-8t+16| \delta t$ $= (0+\frac{1}{3}) + (2-1) + [25t-10t^2+\frac{4}{3}t^3] \Big|_2^3 + [\frac{t^3}{3}-4[t^2]+16t] \Big|_3^4$ $= \frac{1}{3} + 1 + \Big[\big(25(3)-10(3)^2+\frac{4}{3}(3)^3\big) -\big(25(2)-10(2)^2+\frac{4}{3}(2)^3\big)\Big] +$ $+ \Big[\big(\frac{4^3}{3}-4[4^2]+16(4)\big) - \big(\frac{3^3}{3}-4[3^2]+16(3) \big)\Big]$ $= \frac{4}{3} + \Big[\big(75-90+36\big) -\big(50-40+\frac{32}{3}\big)\Big] +$ $+ \Big[\big(\frac{64}{3}-64 +64\big) - \big(9-36+48 \big)\Big]$ $= \frac{4}{3} + \frac{2}{3} = \frac{6}{3} = 2$ $E_{y(t)} = 2$ $P_{y(t)} =\frac{E_{y(t)}}{T_0} = \frac{2}{4} = \frac{1}{2}$