Ejercicio: 1Eva2016TII_T2 LTI CT bloques en paralelo-serie con Laplace , 1Eva2012TII_T4 LTI CT bloques en paralelo-serie con Laplace, 1Eva2011TII_T3 LTI CT H(s) desde expresión con operadores D
Ejercicio resuelto: [ transformada de Laplace ] [integral convolución]
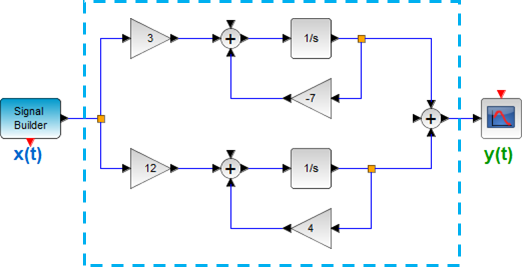
literal a. Funcion H(s) global
en el diagrama se muestran dos sistemas LTIC de primer orden, ambos sistemas se encuentran multiplicados por una constante y en paralelo.
La función de transferencia de un sistema LTIC de primer orden es
H(s) = 1/(s-a)
Con lo que el sistema se puede reescribir como:
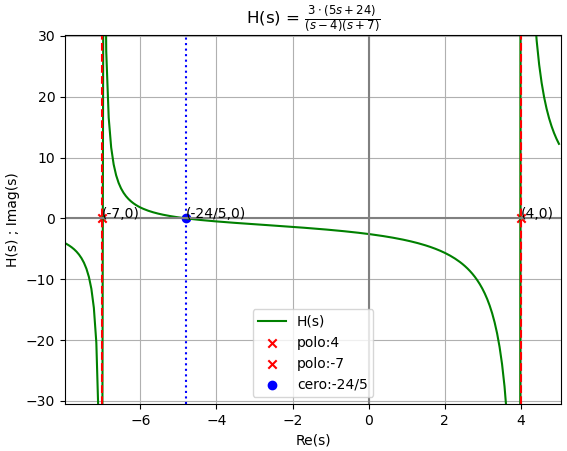
H(s) = 3\frac{1}{s+7} + 12 \frac{1}{s-4}Ceros y polos de H(s)
H(s) = \frac{3(s-4)+12(s+7)}{(s+7)(s-4)} = \frac{3s-12+12s+84}{(s+7)(s-4)} = \frac{15s+72}{(s+7)(s-4)}los ceros se toman del numerador:
15s+72 = 0 s=\frac{-72}{15} = -\frac{24}{5}los polos se toman del denominador:
(s+7)(s-4) = 0 s=-7 ; s= 4literal b. La respuesta impulso h(t)
Los polos tienen signo diferente, lo que indica que el intervalo donde se encuentran incluyen al eje imaginario en el intervalo, por lo que el sistema es BIBO inestable. Por tener un polo a derecha del plano es asintoticamente inestable, su respuesta tiene componentes que crecen en el tiempo.
Como la región de convergencia ROC no se encuentra a la derecha de todos los polos, se tiene concluye que el sistema NO es causal.
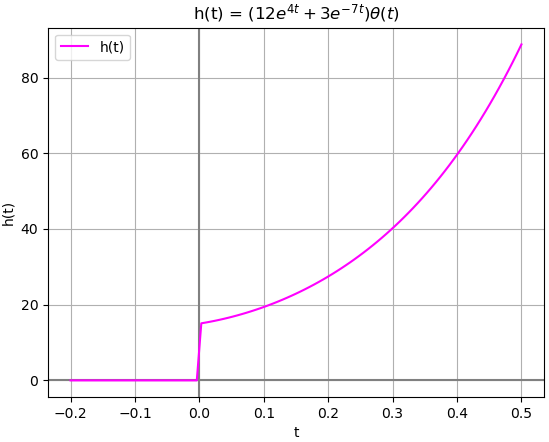
h(t) = \mathscr{L}^{-1} [H(s)] = \mathscr{L}^{-1} \Big[ 3\frac{1}{s+7} + 12 \frac{1}{s-4}\Big] = \mathscr{L}^{-1} \Big[ 3\frac{1}{s+7} \Big] + \mathscr{L}^{-1} \Big[ 12 \frac{1}{s-4}\Big]usando la tabla de transformadas o Sympy de Python
h(t) = 3e^{-7t} \mu (t) + 12 e^{4t} \mu (t)literal c. Salida ante entrada x(t)
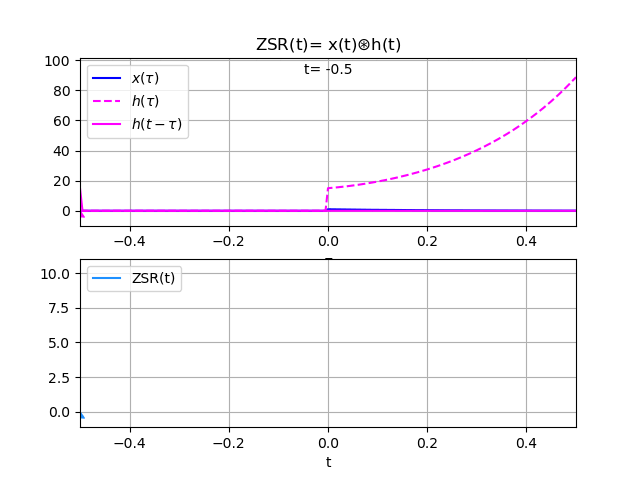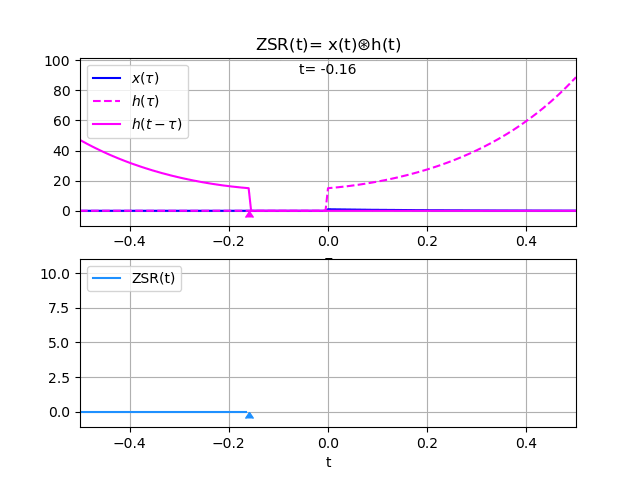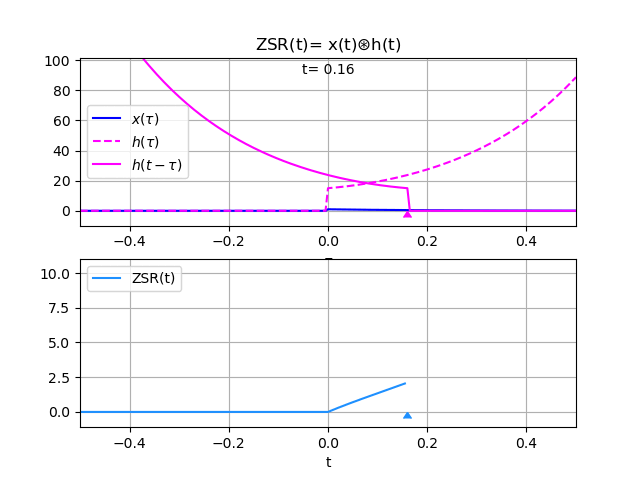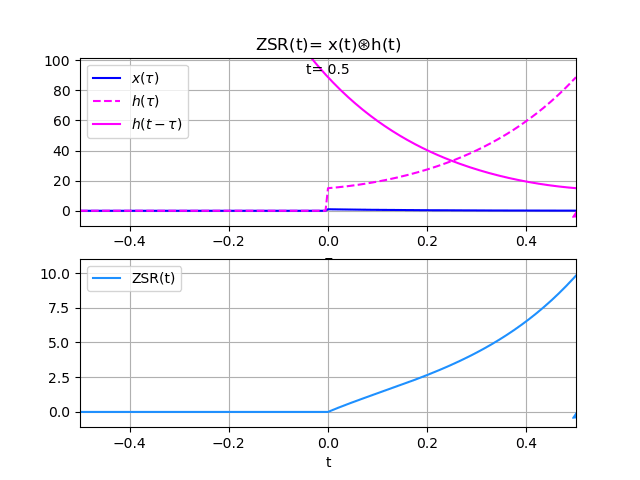
x(t) = e^{-5t} \mu (t) X(s) = \frac{1}{s+5} Y(s) = X(s) H(s) =\frac{1}{s+5} \Bigg[\frac{15s+72}{(s+7)(s-4)}\Bigg] =\frac{15s+72}{(s+5)(s+7)(s-4)}se usa fracciones parciales
=-\frac{3}{2(s+7)} + \frac{1}{6(s+5)}+\frac{4}{3(s-4)} y(t) = \mathscr{L}^{-1} [Y(s)] y(t) = \mathscr{L}^{-1} \Bigg[-\frac{3}{2(s+7)} + \frac{1}{6(s+5)}+\frac{4}{3(s-4)} \Bigg]usando la tabla de transformadas de Laplace :
y(t) = -\frac{3}{2} e^{-7t} \mu (t) + \frac{1}{6}e^{-5t} \mu (t) +\frac{4}{3}e^{4t} \mu (-t)Algoritmo en Python
realizado a partir de LTIC Laplace – Algoritmo Python para analizar estabilidad H(s), Y(s) con entrada cero, estado cero, condiciones iniciales
H(s) = P(s)/Q(s):
3 12
----- + -----
s + 7 s - 4
H(s) en factores:
3*(5*s + 24)
---------------
(s - 4)*(s + 7)
h(t) :
/ 4*t -7*t\
\12*e + 3*e /*Heaviside(t)
polosceros:
Q_polos : {4: 1, -7: 1}
P_ceros : {-24/5: 1}
Estabilidad de H(s):
n_polos_real : 2
n_polos_imag : 0
enRHP : 1
unicos : 0
repetidos : 0
asintota : inestable
X(s):
1
-----
s + 5
Respuesta entrada cero ZIR H(s) y condiciones iniciales
term_cero : 0
ZIR :
0
yt_ZIR :
0
ZSR respuesta estado cero:
ZSR :
3 1 4
- --------- + --------- + ---------
2*(s + 7) 6*(s + 5) 3*(s - 4)
yt_ZSR :
/ 4*t -5*t -7*t\
|4*e e 3*e |
|------ + ----- - -------|*Heaviside(t)
\ 3 6 2 /
Y(s)_total = ZIR + ZSR:
3 1 4
- --------- + --------- + ---------
2*(s + 7) 6*(s + 5) 3*(s - 4)
y(t)_total = ZIR + ZSR:
/ 4*t -5*t -7*t\
|4*e e 3*e |
|------ + ----- - -------|*Heaviside(t)
\ 3 6 2 /
Instrucciones en Python
Usando los bloques desarrollados en la y las funciones resumidas como telg1001.py que pueden ser usados en cada pregunta:
# Y(s) Respuesta total con entada cero y estado cero # Qs Y(s) = Ps X(s) ; H(s)=Ps/Qs # https://blog.espol.edu.ec/telg1001/ import sympy as sym import matplotlib.pyplot as plt import telg1001 as fcnm # INGRESO s = sym.Symbol('s') t = sym.Symbol('t', real=True) d = sym.DiracDelta(t) u = sym.Heaviside(t) # H(s) y estabilidad Hs = 3/(s+7) + 12/(s-4) #Hs = 1+0*s cuando es constante # X(s) Señal de entrada xt = sym.exp(-5*t)*u # condiciones iniciales, [y'(0),y(0)] orden descendente t0 = 0 cond_inicio = [0, 0] # estado cero no se usan # Grafica, intervalo tiempo [t_a,t_b] t_a = -0.2 ; t_b = 0.5 muestras = 101 # 51 resolucion grafica # PROCEDIMIENTO Hs = fcnm.apart_s(Hs) # fracciones parciales Hs_fc = fcnm.factor_exp(Hs) # en factores Hs_Qs2 = fcnm.Q_cuad_s_parametros(Hs_fc) polosceros = fcnm.busca_polosceros(Hs) Q_polos = polosceros['Q_polos'] P_ceros = polosceros['P_ceros'] estable = fcnm.estabilidad_asintotica_s(Q_polos) # H(t) respuesta al impulso ht = 0*s term_suma = sym.Add.make_args(Hs) for term_k in term_suma: ht_k = sym.inverse_laplace_transform(term_k,s,t) # simplifica log(exp()) ej: e**(-2s)/(s**2) if ht_k.has(sym.log): ht_k = sym.simplify(ht_k,inverse=True) ht = ht + ht_k lista_escalon = ht.atoms(sym.Heaviside) ht = sym.expand(ht,t) # terminos suma ht = sym.collect(ht,lista_escalon) # PROCEDIMIENTO Respuesta ZIR, ZSR Xs = fcnm.laplace_transform_suma(xt) # ZIR_s respuesta entrada cero de s sol_ZIR = fcnm.respuesta_ZIR_s(Hs,cond_inicio) ZIR = sol_ZIR['ZIR'] yt_ZIR = sol_ZIR['yt_ZIR'] # ZSR respuesta estado cero, Y(s) a entrada X(s) sol_ZSR = fcnm.respuesta_ZSR_s(Hs,Xs) ZSR = sol_ZSR['ZSR'] yt_ZSR = sol_ZSR['yt_ZSR'] # Respuesta total Y(s) y y(t) Ys = ZIR + ZSR Ys = fcnm.apart_s(Ys) yt = yt_ZIR + yt_ZSR lista_escalon = yt.atoms(sym.Heaviside) yt = sym.collect(yt,lista_escalon) # SALIDA print(' H(s) = P(s)/Q(s):') sym.pprint(Hs) print(' H(s) en factores:') sym.pprint(Hs_fc) if len(Hs_Qs2)>0: print('\nH(s) parámetros cuadraticos:') fcnm.print_resultado_dict(Hs_Qs2) print('\n h(t) :') sym.pprint(ht) print('\npolosceros:') fcnm.print_resultado_dict(polosceros) print('\nEstabilidad de H(s):') for k in estable: print('',k,':',estable[k]) print('\n X(s): ') sym.pprint(Xs) print('\nRespuesta entrada cero ZIR H(s) y condiciones iniciales') if not(sol_ZIR == sym.nan): # existe resultado fcnm.print_resultado_dict(sol_ZIR) else: print(' insuficientes condiciones iniciales') print(' revisar los valores de cond_inicio[]') print('\n ZSR respuesta estado cero:') fcnm.print_resultado_dict(sol_ZSR) print('\n Y(s)_total = ZIR + ZSR:') sym.pprint(Ys) print('\n y(t)_total = ZIR + ZSR:') sym.pprint(yt) # Graficas polos, H(s), con polos h(t) -------- muestras_H = 201 figura_s = fcnm.graficar_Fs(Hs_fc,Q_polos,P_ceros,f_nombre='H',solopolos=True) figura_Hs = fcnm.graficar_Fs(Hs_fc,Q_polos,P_ceros,muestras=muestras_H,f_nombre='H') figura_ht = fcnm.graficar_ft(ht,t_a,t_b,muestras,f_nombre='h') # GRAFICAS y(t),x(t),h(t) --------------------- figura_ft = fcnm.graficar_xh_y(xt,ht,yt,t_a,t_b,muestras) plt.show()
Ejercicio resuelto: [ transformada de Laplace ] [integral convolución]
..
Ejercicio resuelto con integral de convolución, unidad 3
Algoritmo desarrollado con LTI CT Respuesta del Sistema Y(s)=ZIR+ZSR con Sympy-Python
ZIR(t):
0
h(t):
/ 4*t -7*t\
\12*e + 3*e /*Heaviside(t)
ZSR(t):
xh :
4*t -9*tau
12*e *e *Heaviside(tau)*Heaviside(t - tau) +
-7*t 2*tau
+ 3*e *e *Heaviside(tau)*Heaviside(t - tau)
xcausal : True
hcausal : True
[tau_a,tau_b] : [0, t]
intercambia : False
cond_graf : True
ZSR :
/ 4*t -5*t -7*t\
|4*e e 3*e |
|------ + ----- - -------|*Heaviside(t)
\ 3 6 2 /
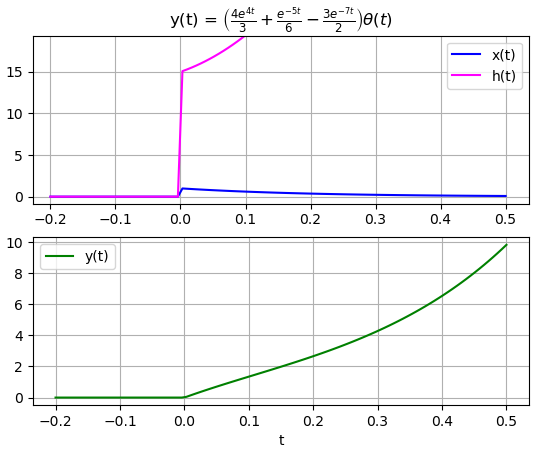
y(t) = ZIR(t)+ZSR(t):
/ 4*t -5*t -7*t\
|4*e e 3*e |
|------ + ----- - -------|*Heaviside(t)
\ 3 6 2 /
Las gráficas resultan iguales a las mostradas
Instrucciones con Python
# Respuesta total del sistema # y(t) = ZIR(t) + ZSR(t) # https://blog.espol.edu.ec/telg1001/lti-ct-yszirzsr-respuesta-del-sistema-con-sympy-python/ # Revisar causalidad de x(t) y h(t) import numpy as np import matplotlib.pyplot as plt import sympy as sym equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] import telg1001 as fcnm # INGRESO t = sym.Symbol('t',real=True) tau = sym.Symbol('tau',real=True) y = sym.Function('y') x = sym.Function('x') h = sym.Function('h') u = sym.Heaviside(t) # ecuacion: lado izquierdo = lado derecho # Left Hand Side = Right Hand Side LHS = sym.diff(y(t),t,2) + 3*sym.diff(y(t),t,1) - 28*y(t) RHS = 15*sym.diff(x(t),t,1,evaluate=False) + 72*x(t) ecuacion = sym.Eq(LHS,RHS) # condiciones iniciales [y'(t0),y(t0)] t0 = 0 cond_inicio = [0,0] # entrada x(t) x = sym.exp(-5*t)*u # grafica intervalo [t_a,t_b] t_a = 0; t_b = .5 muestras = 201 # PROCEDIMIENTO # Respuesta entrada cero ZIR sol_ZIR = fcnm.respuesta_ZIR(ecuacion,cond_inicio,t0) ZIR = sol_ZIR['ZIR'] # Respuesta al impulso h(t) sol_h = fcnm.respuesta_impulso_h(ecuacion) h = sol_h['h'] # respuesta a estado cero ZSR sol_ZSR = fcnm.respuesta_ZSR(x,h) ZSR = sol_ZSR['ZSR'] xh = sol_ZSR['xh'] # respuesta a y(t) = ZIR(t)+ZSR(t) y_total = ZIR+ZSR # revisa si grafica ZSR if not(sol_ZSR['cond_graf']): print('revisar acortar x(t) o h(t) para BIBO') # SALIDA print('\n ZIR(t):') sym.pprint(ZIR) print('\n h(t):') sym.pprint(h) print('\n ZSR(t):') fcnm.print_resultado_dict(sol_ZSR) if sol_ZSR['hcausal']==False: print('revisar causalidad de h(t)') if sol_ZSR['xcausal']==False: print('revisar causalidad de x(t)') if sol_ZSR['intercambia']: print('considere intercambiar h(t)con x(t)') if not(sol_ZSR['cond_graf']): print('revisar acortar x(t) o h(t) para BIBO') print('\n y(t) = ZIR(t)+ZSR(t):') sym.pprint(y_total) # GRAFICA figura_ZIR = fcnm.graficar_ft(ZIR,t_a,t_b, muestras,'ZIR') figura_h = fcnm.graficar_ft(h,t_a,t_b, muestras,'h') # grafica animada de convolución n_archivo = '' # sin crear archivo gif animado #n_archivo = '1Eva2016TII_T2_ZSR' # requiere 'imagemagick' if sol_ZSR['cond_graf']: fig_ZSR = fcnm.graficar_xh_y(x,h,ZSR,t_a,t_b, muestras,y_nombre='ZSR') fig_ytotal = fcnm.graficar_xhy(ZIR,ZSR,y_total,t_a,t_b, muestras,x_nombre='ZIR', h_nombre='ZSR',y_nombre='y') figura_animada = fcnm.graf_animada_xh_y(x,h,ZSR,-t_b,t_b, muestras, reprod_x = 4,y_nombre='ZSR', archivo_nombre = n_archivo) plt.show()