Publicado en por Edison Del Rosario

s2Eva2010TI_T1 LTI DT Bloques de H[z] para ecuación de diferencias

Ejercicio: 2Eva2010TI_T1 LTI DT Bloques de H[z] para ecuación de diferencias

2E2010TI_T1 LTID diagrama1

litera a. La función de transferencia H(z)

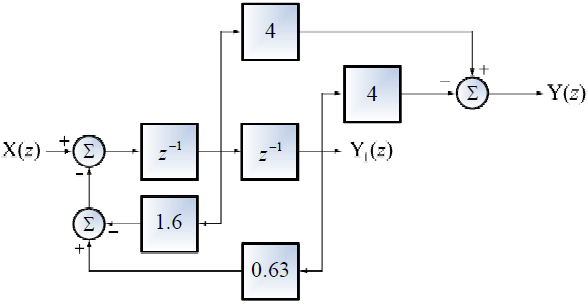
El diagrama mostrado se reordena y añade anotaciones para facilitar la escritura de la ecuación de diferencias:

Dado que hay dos bloques (1/z) o de retraso hacia abajo, se identifica que los polinomios son de segundo orden (N=2).

Los coeficientes de retraso se leen de arriba hacia abajo como a0,-a1,-a2 ordenados en la siguiente tabla:

coeficientes
retraso adelanto
a0 = 1 b0 = 0
a1 = -(1.6) = -1.6 b1 = 4
a2 = -(-0.63) = 0.63 b2 = -4

Se aplica lo mismo para los coeficientes de adelanto y se completa el modelo para los polinomios del numerador y denominador:

H[z] = \frac{b_0 z^N +b_1 z^{N-1} + \text{ ... } + b_{N-1} z + b_N}{z^N + a_1 z^{N-1} +\text{ ... } + a_{N-1}z +a_N} H[z] = \frac{4z-4}{z^2 -1.6 z + 0.63}

Con el polinomio del denominador Qz  se encuentran las raíces

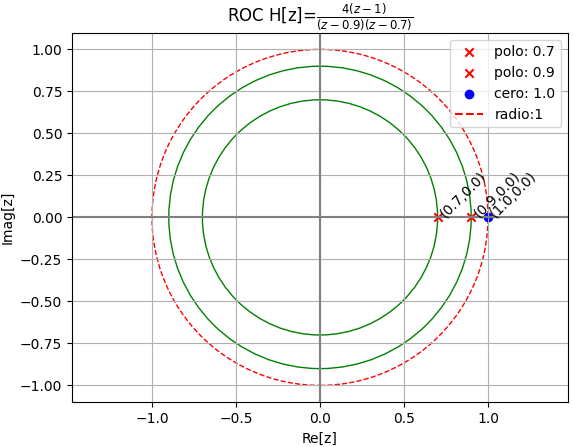
polos: {0.70: 1, 0.90: 1}

se aplican fracciones parciales modificadas al dividir cada lado para z,

\frac{H[z]}{z} = \frac{4}{z}\frac{z-1}{(z-0.7)(z-0.9)} = \frac{k_1}{z-0.7} +\frac{k_2}{z-0.9}+\frac{k_3}{z}

aplicando el método de Heaviside:

k_1 = \frac{4}{z}\frac{z-1}{\cancel{(z-0.7)}(z-0.9)}\Big|_{z=0.7} = \frac{4}{0.7}\frac{(0.7)-1}{((0.7)-0.9)} = 8.5714 k_2 = \frac{4}{z}\frac{z-1}{(z-0.7)\cancel{(z-0.9)}}\Big|_{z=0.9} = \frac{4}{0.9}\frac{(0.9)-1}{((0.9)-0.7)} = -2.2222 k_3 = \frac{4}{\cancel{z}}\frac{z-1}{(z-0.7)(z-0.9)}\Big|_{z=0} = 4\frac{(0)-1}{((0)-0.7)((0)-0.9)} = -6.3492 \frac{H[z]}{z} = \frac{8.5714}{z-0.7} -\frac{2.2222}{z-0.9}-\frac{6.3492}{z}

restaurando a fracciones parciales al multiplicar por z

H[z] = \frac{8.5714z}{z-0.7} -\frac{2.2222z}{z-0.9}-6.3492

usando la tabla de transformadas z

h[n] = 8.5714 (0.7)^n \mu[n] -2.2222(0.9)^n \mu[n] -6.3492 \delta[n]

Algoritmo en Python

Usando el algoritmo de la sección X[z] Fracciones parciales modificadas con Python

con entrada:

Pz = 4*z-4
Qz = z**2-1.6*z+0.63

y resultado:

 Hz:
     4*z - 4     
-----------------
 2               
z  - 1.6*z + 0.63

 Hz en fracciones parciales
8.57142857142857*z   2.22222222222222*z                   
------------------ - ------------------ - 6.34920634920635
     z - 0.7              z - 0.9                         

 Hz en factores
     4*(z - 1)     
-------------------
(z - 0.9)*(z - 0.7)

 {Q_polos:veces}: {0.700000000000000: 1, 0.900000000000000: 1}
 {P_ceros:veces}: {1: 1}

estabilidad asintótica en z:
circ1_dentro : 2
circ1_repetidos : 0
circ1_sobre : 0
circ1_fuera : 0
unicos : 2
repetidos : 0
asintota : estable

 h[n]:
/                    n                       n\                               
\8.57142857142857*0.7  - 2.22222222222222*0.9 /*Heaviside(n) 

  - 6.34920634920635*DiracDelta(n)

señal discreta h[n]
n   : [0 1 2 3 4 5 6 7 8 9]
h[n]: [ 0.   4.   2.4   1.32   0.6   0.1284
       -0.17256    -0.356988   -0.462468   -0.51504636]

2Eva2010TI_T1 Hz polos01

2Eva2010TI_T1 h[n]

Observaciones:

Las raíces características o frecuencias naturales del sistema se encuentran dentro del círculo de radio unitario. El sistema es asintóticamente estable, que implica que es BIBO estable.

literal c. Ecuación de diferencias

H[z] = \frac{4z-4}{z^2 -1.6 z + 0.63} Y[z](z^2 -1.6 z+ 0.63) = (4z-4)X[z] y[n+2] - 1.6 y[n+1] + 0.63y[n] = 4x[n+1]-4x[n]

literal d. entrada x[n]

x(t) = cos(1500t) = cos (2πf) con intervalo de muestreo Ts = 0.0015 = 1/fs.

De la señal de entrada se tiene que 2πf=1500, por lo que f = 1500/(2π)

Para un buen muestreo de la señal de entrada, se debe cumplir la frecuencia de Nyquist, es decir fs>2f

fs = \frac{1}{0.0015} = 666.66 \text{ ; } f= \frac{1500}{2 \pi}=238.73 fs > 2*f = 2(238.73) = 477.46

que cumple con la frecuencia mínima de muestreo y no se presentan inconvenientes para el funcionamiento de la señal por sub-muestreo

Instrucciones en Python

# Transformada z- Fracciones parciales
# https://blog.espol.edu.ec/telg1001/lti-dt-transformada-z-xz-fracciones-parciales-con-python/
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt
import telg1001 as fcnm
#sym.SYMPY_DEBUG=True

# INGRESO
z = sym.Symbol('z')
n = sym.Symbol('n', real=True)

# coeficientes como racional en dominio 'ZZ' enteros
Pz = 4*z-4
Qz = z**2-1.6*z+0.63

F = Pz/Qz

# para graficar
f_nombre = 'H'    # nombre de función[z]: H,X,Y, etc
muestras_fn = 10  # muestras para f[n]

# PROCEDIMIENTO
Fz  = fcnm.apart_z(F)
Fz_factor = sym.factor(F.evalf())
Fz_factor = fcnm._round_float_is_int(Fz_factor)

# polos y ceros de Hz
[P,Q] = F.as_numer_denom()
P = sym.poly(P,z)
Q = sym.poly(Q,z)
P_ceros = sym.roots(P)
Q_polos = sym.roots(Q)
estable_z = fcnm.estabilidad_asintotica_z(Q_polos)

# Inversa de transformada z
fn = 0*n ; Fz_revisar = [] ; Qz2_term =[]
term_sum = sym.Add.make_args(Fz)
for term_k in term_sum:
    term_kn = fcnm.inverse_z_transform(term_k,z,n)
    if type(term_kn)==tuple:
        fn = fn + term_kn[0]
    elif term_kn is not None:
        fn = fn + term_kn
    elif term_kn is None:
        f_noeval = f_noeval + term_k
    Qz2 = fcnm.Q_cuad_z_parametros(term_k)
    if Qz2:
        Qz2_term.append(Qz2)
fn = fn.collect(sym.Heaviside(n))
fn = fn.collect(sym.DiracDelta(n))
fn = fcnm._round_float_is_int(fn)

# SALIDA
print('\n '+f_nombre+'z:')
sym.pprint(F)
print('\n '+f_nombre+'z en fracciones parciales')
sym.pprint(Fz)
print('\n '+f_nombre+'z en factores')
sym.pprint(Fz_factor)
print('\n {Q_polos:veces}:',Q_polos)
print(' {P_ceros:veces}:',P_ceros)
if len(Qz2_term)>0:
    print('\nparametros cuadraticos: ')
    for i in range(0,len(Qz2_term),1):
        for unterm in Qz2_term[i]:
            print(' termino:',unterm)
            fcnm.print_resultado_dict(Qz2_term[i][unterm])
print('\nestabilidad asintótica en z:')
fcnm.print_resultado_dict(estable_z)
print('\n '+f_nombre.lower()+'[n]:')
sym.pprint(fn)
if len(Fz_revisar)>0:
    print('revisar terminos sin transformada de tabla:')
    for un_term in Fz_revisar:
        print(un_term)

# # GRAFICA  -----------
fig_ROC = fcnm.graficar_Fz_polos(Fz_factor,Q_polos,P_ceros,
                      muestras=101,f_nombre=f_nombre)

fig_Fz = fcnm.graficar_Fs(Fz_factor,Q_polos,P_ceros,
                     muestras=101,
                     f_nombre=f_nombre)

# graficar f[n] -------
f_n = sym.lambdify(n,fn.expand(),modules=fcnm.equivalentes)
ki  = np.arange(0,muestras_fn,1.0)
fi  = f_n(ki)

print('\nseñal discreta '+f_nombre.lower()+'[n]')
print('n   :',ki)
print(f_nombre.lower()+'[n]:',fi)

# graficar f[n]
fig_fn, grafxn = plt.subplots()
plt.axvline(0,color='grey')
plt.stem(ki,fi)
plt.grid()
plt.xlabel('n')
plt.ylabel(f_nombre.lower()+'[n]')
etiqueta = r''+f_nombre.lower()+'[n]= $'+str(sym.latex(fn))+'$'
plt.title(etiqueta)

plt.show()