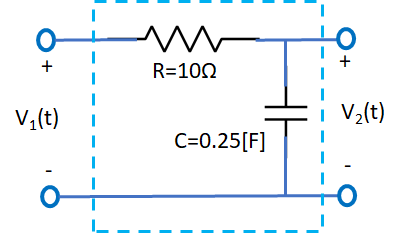
Ejercicio 2Eva2016TII_T2 LTI CT Circuito RC respuesta de frecuencia H(ω), impulso h(t)
literal a
v 1 ( t ) = v R ( t ) + v C ( t ) v_1 (t) = v_R (t) +v_C (t) v 1 ( t ) = v R ( t ) + v C ( t ) v 1 ( t ) = R i ( t ) + v 2 ( t ) v_1 (t) = R i(t) +v_2 (t) v 1 ( t ) = R i ( t ) + v 2 ( t ) i ( t ) = C δ v 2 ( t ) δ t i(t) = C \frac{\delta v_2 (t)}{\delta t} i ( t ) = C δ t δ v 2 ( t ) v 2 ( t ) = R C δ v 2 ( t ) δ t + v 2 ( t ) v_2(t) = RC \frac{\delta v_2 (t)}{\delta t} +v_2 (t) v 2 ( t ) = R C δ t δ v 2 ( t ) + v 2 ( t ) V 1 ( ω ) = j ω R C V 2 ( ω ) + V 2 ( ω ) = V 2 ( ω ) [ 1 + j ω R C ] V_1 (\omega) = j \omega RC V_2 (\omega) + V_2(\omega) = V_2(\omega) [1+j\omega RC] V 1 ( ω ) = j ω R C V 2 ( ω ) + V 2 ( ω ) = V 2 ( ω ) [ 1 + j ω R C ] H ( ω ) = V 2 ( ω ) V 1 ( ω ) = 1 1 + j ω R C = 1 1 + j ω ω c H(\omega) = \frac{V_2 (\omega)}{V_1(\omega)} = \frac{1}{1+j\omega RC} = \frac{1}{1+j\frac{\omega}{\omega_c}} H ( ω ) = V 1 ( ω ) V 2 ( ω ) = 1 + j ω R C 1 = 1 + j ω c ω 1 ω c = 1 R C \omega _c = \frac{1}{RC} ω c = R C 1 H ( ω ) = V 2 ( ω ) V 1 ( ω ) = 1 1 + j ω 2 H(\omega) =\frac{V_2(\omega)}{V_1(\omega)} = \frac{1}{1+j\frac{\omega}{2}} H ( ω ) = V 1 ( ω ) V 2 ( ω ) = 1 + j 2 ω 1 { ∣ H ( ω ) = 1 1 + ( ω 2 ) 2 θ H ( ω ) = − t g − 1 ( ω 2 ) \begin{cases} |H(\omega) = \frac{1}{\sqrt{1+\big( \frac{\omega}{2}\big)^2}} \\ \theta_{H(\omega)} = -tg^{-1} \big( \frac{\omega}{2}\big) \end{cases} ⎩ ⎪ ⎨ ⎪ ⎧ ∣ H ( ω ) = 1 + ( 2 ω ) 2 1 θ H ( ω ) = − t g − 1 ( 2 ω ) ω c = 1 R C \omega _c = \frac{1}{RC} ω c = R C 1 literal c
La respuesta impulso del filtro LPF, se obtiene mediante:
h ( t ) = F − 1 [ H ( ω ) ] = F − 1 [ 1 1 + j ( ω / 2 ) ] h(t) = \mathcal{F}^{-1} \Big[ H(\omega) \Big] = \mathcal{F}^{-1} \Big[ \frac{1}{1+j(\omega /2)} \Big] h ( t ) = F − 1 [ H ( ω ) ] = F − 1 [ 1 + j ( ω / 2 ) 1 ] = 2 F − 1 [ 1 j ω + 2 ] =2\mathcal{F}^{-1} \Big[ \frac{1}{j\omega +2} \Big] = 2 F − 1 [ j ω + 2 1 ] h ( t ) = 2 e 2 t μ ( t ) h(t)=2e^{2t}\mu (t) h ( t ) = 2 e 2 t μ ( t ) literal d
Método 1: usando la respuesta de frecuencia
{ ∣ H ( ω ) = 1 1 + ( ω 2 ) 2 θ H ( ω ) = − t g − 1 ( ω 2 ) \begin{cases} |H(\omega) = \frac{1}{\sqrt{1+\big( \frac{\omega}{2}\big)^2}} \\ \theta_{H(\omega)} = -tg^{-1} \big( \frac{\omega}{2}\big) \end{cases} ⎩ ⎪ ⎨ ⎪ ⎧ ∣ H ( ω ) = 1 + ( 2 ω ) 2 1 θ H ( ω ) = − t g − 1 ( 2 ω ) { ∣ H ( 5 0 ) = 1 1 + ( 5 0 2 ) 2 = 1 ( 6 2 6 ) θ H ( ω ) = − t g − 1 ( 5 0 2 ) = − 8 7 . 7 \begin{cases} |H(50) = \frac{1}{\sqrt{1+\big( \frac{50}{2}\big)^2}} = \frac{1}{\sqrt(626)} \\ \theta_{H(\omega)} = -tg^{-1} \big( \frac{50}{2}\big) = -87.7\end{cases} ⎩ ⎪ ⎨ ⎪ ⎧ ∣ H ( 5 0 ) = 1 + ( 2 5 0 ) 2 1 = ( 6 2 6 ) 1 θ H ( ω ) = − t g − 1 ( 2 5 0 ) = − 8 7 . 7 v 2 ( t ) = ∣ H ( 5 0 ) ∣ sin ( 5 0 t + θ H ( 5 0 ) ) v_2(t) = |H(50)| \sin \big(50t+\theta_{H(50)} \big) v 2 ( t ) = ∣ H ( 5 0 ) ∣ sin ( 5 0 t + θ H ( 5 0 ) ) v 2 ( t ) = 1 ( 6 2 6 ) sin ( 5 0 t − 8 7 . 7 ) ) v_2(t) = \frac{1}{\sqrt(626)} \sin \big(50t-87.7) \big) v 2 ( t ) = ( 6 2 6 ) 1 sin ( 5 0 t − 8 7 . 7 ) ) método 2:
V 2 ( ω ) = V 1 ( ω ) H ( ω ) V_2(\omega ) = V_1(\omega) H(\omega) V 2 ( ω ) = V 1 ( ω ) H ( ω ) V 1 ( ω ) = F [ v 1 ( t ) ] = F [ sin ( 5 0 t ) ] V_1 (\omega) = \mathcal{F}[v_1(t) ] = \mathcal{F} [ \sin (50t) ] V 1 ( ω ) = F [ v 1 ( t ) ] = F [ sin ( 5 0 t ) ] = j π δ ( ω + 5 0 ) − j π δ ( ω − 5 0 ) = j \pi \delta (\omega +50) - j \pi \delta (\omega-50) = j π δ ( ω + 5 0 ) − j π δ ( ω − 5 0 ) V 2 ( ω ) = V 1 ( ω ) H ( ω ) V_2 (\omega) = V_1(\omega) H(\omega) V 2 ( ω ) = V 1 ( ω ) H ( ω ) V 2 ( ω ) = [ j π δ ( ω + 5 0 ) − j π δ ( ω − 5 0 ) ] [ 1 1 + j ( ω / 2 ) ] V_2 (\omega) = \Big[ j \pi \delta (\omega +50) - j \pi \delta (\omega-50) \Big] \Big[ \frac{1}{1+j(\omega/2)} \Big] V 2 ( ω ) = [ j π δ ( ω + 5 0 ) − j π δ ( ω − 5 0 ) ] [ 1 + j ( ω / 2 ) 1 ] = j π [ δ ( ω + 5 0 ) 1 1 + j ( ω / 2 ) − δ ( ω − 5 0 ) 1 1 + j ( ω / 2 ) ] = j \pi \Big[ \delta (\omega + 50)\frac{1}{1+j(\omega /2)} - \delta (\omega - 50)\frac{1}{1+j(\omega /2)}\Big] = j π [ δ ( ω + 5 0 ) 1 + j ( ω / 2 ) 1 − δ ( ω − 5 0 ) 1 + j ( ω / 2 ) 1 ] = j π [ δ ( ω + 5 0 ) 1 1 + j ( 5 0 / 2 ) − δ ( ω − 5 0 ) 1 1 + j ( 5 0 / 2 ) ] = j \pi \Big[ \delta (\omega + 50)\frac{1}{1+j(50 /2)} - \delta (\omega - 50)\frac{1}{1+j(50 /2)}\Big] = j π [ δ ( ω + 5 0 ) 1 + j ( 5 0 / 2 ) 1 − δ ( ω − 5 0 ) 1 + j ( 5 0 / 2 ) 1 ] = j π [ δ ( ω + 5 0 ) 1 + j 2 5 6 2 6 − δ ( ω − 5 0 ) 1 − j 2 5 6 2 6 ] = j \pi \Big[ \delta (\omega + 50)\frac{1+j25}{626} - \delta (\omega - 50)\frac{1-j25}{626}\Big] = j π [ δ ( ω + 5 0 ) 6 2 6 1 + j 2 5 − δ ( ω − 5 0 ) 6 2 6 1 − j 2 5 ] = j π 6 2 6 [ δ ( ω + 5 0 ) − δ ( ω − 5 0 ) + j 2 5 δ ( ω + 5 0 ) + j 2 5 δ ( ω − 5 0 ) ] = j \frac{\pi}{626} \Big[ \delta (\omega + 50) - \delta (\omega - 50) + j25 \delta (\omega + 50) + j25 \delta (\omega - 50)\Big] = j 6 2 6 π [ δ ( ω + 5 0 ) − δ ( ω − 5 0 ) + j 2 5 δ ( ω + 5 0 ) + j 2 5 δ ( ω − 5 0 ) ] = 1 6 2 6 [ j π δ ( ω + 5 0 ) − j π δ ( ω − 5 0 ) ] − 2 5 6 2 6 [ π δ ( ω + 5 0 ) + π δ ( ω − 5 0 ) ] = \frac{1}{626} \Big[ j\pi \delta (\omega + 50) - j \pi \delta(\omega - 50)\Big] - \frac{25}{626} \Big[ \pi \delta (\omega + 50) +\pi \delta(\omega - 50)\Big] = 6 2 6 1 [ j π δ ( ω + 5 0 ) − j π δ ( ω − 5 0 ) ] − 6 2 6 2 5 [ π δ ( ω + 5 0 ) + π δ ( ω − 5 0 ) ] v 2 ( t ) = F − 1 [ V 2 ( ω ) ] v_2(t) = \mathcal{F}^{-1} [V_2 (\omega)] v 2 ( t ) = F − 1 [ V 2 ( ω ) ] = 1 6 2 6 F − 1 [ [ j π δ ( ω + 5 0 ) − j π δ ( ω − 5 0 ) ] − 2 5 [ π δ ( ω + 5 0 ) + π δ ( ω − 5 0 ) ] ] = \frac{1}{626} \mathcal{F}^{-1}\Bigg[ \Big[ j\pi \delta (\omega + 50) - j \pi \delta(\omega - 50)\Big] - 25 \Big[ \pi \delta (\omega + 50) +\pi \delta(\omega - 50)\Big] \Bigg] = 6 2 6 1 F − 1 [ [ j π δ ( ω + 5 0 ) − j π δ ( ω − 5 0 ) ] − 2 5 [ π δ ( ω + 5 0 ) + π δ ( ω − 5 0 ) ] ] v 2 ( t ) = 1 6 2 6 [ sin ( 5 0 t ) − 2 5 cos ( 5 0 t ) ] v_2(t) = \frac{1}{626} \Big[ \sin (50t) - 25 \cos (50t) \Big] v 2 ( t ) = 6 2 6 1 [ sin ( 5 0 t ) − 2 5 cos ( 5 0 t ) ] usando fasores:
v 2 ( t ) = 1 6 2 6 cos ( 5 0 t − 1 7 7 . 7 0 9 ) = 1 6 2 6 sin ( 5 0 t − 8 7 . 7 0 ) v_2(t) = \frac{1}{626} \cos (50t-177.709) = \frac{1}{626} \sin (50t-87.70) v 2 ( t ) = 6 2 6 1 cos ( 5 0 t − 1 7 7 . 7 0 9 ) = 6 2 6 1 sin ( 5 0 t − 8 7 . 7 0 ) En la salida, existe un factor de atenuación de 0.04 y un retardo de 87.70°.
