s3Eva2016TI_T2 LTI CT sub-sistemas h(t) multiplicados con Fourier

Ejercicio: 3Eva2016TI_T2 LTI CT sub-sistemas h(t) multiplicados con Fourier

a. Determinar la energía contenida en la señal h(t)

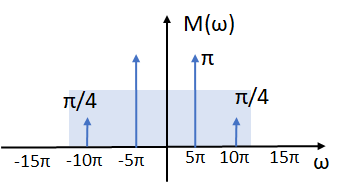
$h(t) = \frac{\sin (11 \pi t)}{\pi t}$ $E_{h(t)} = \int_{-\infty}^{\infty} |h(t)|^2 \delta t = \frac{1}{2\pi} \int_{-\infty}^{\infty}|H(\omega)|^2 \delta \omega$ $= \frac{1}{2\pi} \int_{-11\pi}^{11\pi}|1|^2 \delta \omega = \frac{1}{2\pi} \omega \Big|_{-11\pi}^{11\pi}$ $= \frac{1}{2\pi} \big(11\pi-(-11\pi)\big)$ $= \frac{1}{2\pi} 2\big(11\pi\big) = 11$

b. Determinar, esquematizar y etiquetar el espectro de Fourier de la señal m(t). Es decir M(ω) vs ω.

$X(\omega) = \mathscr{F} \Big[\sum_{i=1}^{\infty} \frac{1}{k^2} \cos(5k\pi t) \Big]$ $= \sum_{i=1}^{\infty} \frac{1}{k^2} \mathscr{F} \Big[\cos (5k\pi t) \Big]$ $= \sum_{i=1}^{\infty} \frac{1}{k^2} \Big[\pi \delta (\omega +5k\pi) + \pi \delta (\omega -5k\pi) \Big]$ $X(\omega) = \pi \sum_{i=1}^{\infty} \frac{1}{k^2} \Big[\delta (\omega +5k\pi) +\delta (\omega -5k\pi) \Big]$

Para el caso de la función de transferencia H(ω) que representa un filtro pasabajo LPF,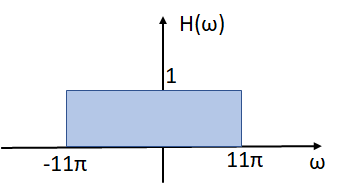

$H(\omega) = \mathscr{F} \Big[\frac{\cos (11 \pi t)}{\pi t} \Big] = p_{11\pi}(\omega)$ $-11\pi \lt \omega \lt 11\pi$ $M(\omega) = X( \omega ) H( \omega )$ $= p_{11\pi}(\omega) \sum_{i=1}^{\infty} \frac{1}{k^2} \pi\Big[\delta (\omega +5k\pi) +\delta (\omega -5k\pi) \Big]$

por el filtro pasabajo  LPF se limitan las señales hasta k=2

$= \sum_{i=1}^{2} \frac{1}{k^2} \pi\Big[\delta (\omega +5k\pi) +\delta (\omega -5k\pi) \Big]$ $= \pi \frac{1}{1^2} \Big[\delta (\omega +5\pi) +\delta (\omega -5\pi) \Big]$ $+ \pi \frac{1}{2^2} \Big[\delta (\omega +5(2)\pi) +\delta (\omega -5(2)\pi) \Big]$ $= \pi \delta (\omega +5\pi) +\pi \delta (\omega -5\pi)$ $+ \frac{\pi}{4} \delta (\omega +10\pi) +\frac{\pi}{4} \delta (\omega -10\pi)$

c. Determinar, esquematizar y etiquetar el espectro de Fourier de la señal n(t). Es decir N(ω) vs ω

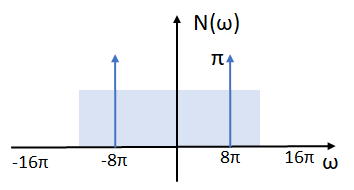
$N(\omega) = G( \omega ) H( \omega )$ $N(\omega) = G( \omega ) \mathscr{F} \Big[\sum_{k=1}^{10} \cos (8k \pi t) \Big]$ $= p_{11\pi}(\omega) \sum_{i=1}^{10} \pi\Big[\delta (\omega +8k\pi) +\delta (\omega -8k\pi) \Big]$

por el filtro pasabajo LPF se limitan las señales hasta k=1

$= \pi \sum_{i=1}^{1} \Big[\delta (\omega +8k\pi) +\delta (\omega -8k\pi) \Big]$ $= \pi \Big[\delta (\omega +8\pi) +\delta (\omega -8\pi) \Big]$ $= \pi \delta (\omega +8\pi) + \pi\delta (\omega -8\pi)$

d. Determinar la potencia de la señal de salida y(t) y la representación de su espectro de Series de Fourier complejas exponenciales. Indique también el orden de los armónicos que están presentes en dicha salida.

$Z(\omega) = \mathscr{F}[m(t) n(t)] = \frac{1}{2 \pi} M(\omega) \circledast N(\omega)]$ $= \frac{1}{2 \pi} \Big[\pi \delta (\omega +5\pi) +\pi \delta (\omega -5\pi) +$ $+\frac{\pi}{4} \delta (\omega +10\pi) +\frac{\pi}{4} \delta (\omega -10\pi)\Big] \circledast \Big[ \pi \delta (\omega +8\pi) + \pi\delta (\omega -8\pi) \Big]$

se obtiene factor común π,  para simplificar

$Z(\omega) = \frac{\pi^2}{2\pi} \Big[\delta (\omega +5\pi) + \delta (\omega -5\pi) +$ $+\frac{1}{4} \delta (\omega +10\pi) +\frac{1}{4} \delta (\omega -10\pi)\Big] \circledast \Big[ \delta (\omega +8\pi) + \delta (\omega -8\pi) \Big]$ $= \frac{\pi}{2} \Big[\delta (\omega +5\pi+8\pi) + \delta (\omega -5\pi+8\pi) +$ $+\frac{1}{4} \delta (\omega +10\pi +8\pi) +\frac{1}{4} \delta (\omega -10\pi +8\pi)$ $+\delta (\omega +5\pi-8\pi) + \delta (\omega -5\pi-8\pi) +$ $+\frac{1}{4} \delta (\omega +10\pi -8\pi) +\frac{1}{4} \delta (\omega -10\pi -8\pi) \Big]$ $Z(\omega) = \frac{\pi}{2} \Big[\delta (\omega +13\pi) + \delta (\omega +3\pi) +$ $+\frac{1}{4}\delta (\omega +18\pi) +\frac{1}{4} \delta (\omega -2\pi)$ $+ \delta (\omega -3\pi) + \delta (\omega -13\pi) +$ $+\frac{1}{4} \delta (\omega +2\pi) +\frac{1}{4} \delta (\omega -18\pi)\Big]$

d. Determinar la potencia de la señal de salida y(t) y la representación de su espectro de Series de Fourier complejas exponenciales. Indique también el orden de los armónicos que están presentes en dicha salida.

$Y(\omega) = Z(\omega) H(\omega)] = p_{11\pi}(\omega)Z(\omega)$

Las frecuencias superiores a 11ω no pasan por el filtro LPF

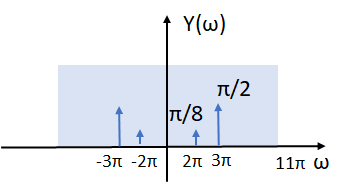
$Z(\omega) = \frac{\pi}{2} \Big[\cancel{\delta (\omega +13\pi)} + \delta (\omega +3\pi) +$ $+\cancel{\frac{1}{4}\delta (\omega +18\pi)} +\frac{1}{4} \delta (\omega -2\pi)$ $+ \delta (\omega -3\pi) + \cancel{\delta (\omega -13\pi)} +$ $+\frac{1}{4} \delta (\omega +2\pi) +\cancel{\frac{1}{4} \delta (\omega -18\pi)}\Big]$ $Y(\omega)= \frac{\pi}{2} \Big[\delta (\omega +3\pi) + \delta (\omega -3\pi) +$ $+\frac{1}{4} \delta (\omega +2\pi) + \frac{1}{4} \delta (\omega -2\pi)\Big]$ $Y(\omega)= \frac{\pi}{2}\delta (\omega +3\pi) + \frac{\pi}{2}\delta (\omega -3\pi) +$ $+\frac{\pi}{8} \delta (\omega +2\pi) + \frac{\pi}{8} \delta (\omega -2\pi)$

ordenando y agrupando para obtener la inversa de la transformada,

$Y(\omega)= \frac{1}{8} \pi \Big[ \delta (\omega +2\pi) + \delta (\omega -2\pi) \Big]$ $+\frac{1}{2} \pi\Big[\delta (\omega +3\pi) + \delta (\omega -3\pi) \Big]$

 

$y(t) = \mathscr{F}^{-1}\Big[ Y(\omega) \Big]$ $y(t) = \frac{1}{8}\cos (2 \pi t) + \frac{1}{2}\cos (3 \pi t)$

para determinar las frecuencias fundamentales de y(t) se tiene:

$\omega_1 = 2\pi f = \frac{2\pi}{T_1} =2 \pi$ $T_1 = \frac{2\pi}{2\pi} =1$ $\omega_2 = 2\pi f = \frac{2\pi}{T_2} =3 \pi$ $T_2 = \frac{2\pi}{3\pi} = \frac{2}{3}$ $\frac{T_1}{T_2} = \frac{1}{2/3} =\frac{3}{2}$

la relación entre los periodos fundamentales es racional, se tiene que la señal de salida y(t) es periódica.

$2T_1 = 3T_2 =T_0$ $2(1) = 3 \frac{2}{3} = 2 =T_0$ $\omega_0 = \frac{2\pi}{T_0} =\frac{2\pi}{2} = \pi$

los armónicos se pueden obtener observando la gráfica de y(ω):

k₁ = 2, k₂=3

para la potencia de la señal de salida y(t) se puede aplicar la relación de Parseval, siendo C_k los coeficientes de cada cos() para cada ω_k, y C₀ es cero por no tener componente en ω₀=π

$P_{y(t)} = C_o^2 + \frac{1}{2} \sum_{k=1}^{\infty} |C_k|^2$ $=(0)^2 + \frac{1}{2} \Big[ \Big(\frac{1}{8}\Big)^2 + \Big( \frac{1}{2}\Big) ^2 \Big]$ $=(0)^2 + \frac{1}{2} \Big[ \frac{1}{64} +\frac{1}{4} \Big] = \frac{1}{2}\Big(\frac{1}{4}\Big) \Big[ \frac{1}{16} +1 \Big]$ $= \frac{1}{8} \frac{17}{16} = \frac{17}{128}$