Ejercicio: 3Eva2016TI_T4 rampa(ω) – transformada inversa de Fourier
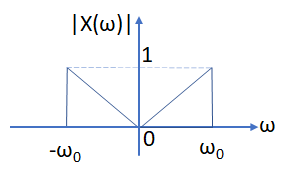
la función de magnitud |X(ω)| es par en el eje vertical,
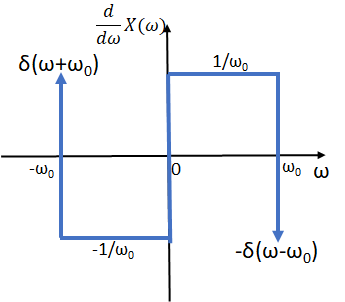
usando la derivada de |X(ω)|,
la expresión de la gráfica usando impulsos y rectángulos en dominio ω es,
\frac{\delta}{\delta \omega}X(\omega) = \delta( \omega +\omega_0) - \frac{1}{\omega_0} P_{\omega_0/2}\Big( \omega +\frac{\omega_0}{2}\Big) + \frac{1}{\omega_0} P_{\omega_0/2}\Big( \omega -\frac{\omega_0}{2}\Big) - \delta( \omega - \omega_0)aplicando la transformada inversa de Fourier
\mathscr{F} ^{-1} \Big[ \frac{\delta}{\delta \omega}X(\omega) \Big] = \mathscr{F} ^{-1} \Big[\delta( \omega +\omega_0) - \frac{1}{\omega_0} P_{\omega_0/2}\Big( \omega +\frac{\omega_0}{2}\Big) \Big] + \mathscr{F} ^{-1} \Big[\frac{1}{\omega_0} P_{\omega_0/2}\Big( \omega -\frac{\omega_0}{2}\Big) - \delta( \omega - \omega_0) \Big]si se realiza por partes, y considerando solo la gráfica de magnitud |X(ω)|
\mathscr{F} ^{-1} \Big[ \frac{\delta}{\delta \omega}X(\omega) \Big] = -jtx_1(t) \mathscr{F} ^{-1} \Big[\delta( \omega +\omega_0)\Big] = \frac{1}{2\pi} e^{-j\omega_0 t} \mathscr{F} ^{-1} \Big[\frac{1}{\omega_0} P_{\omega_0/2}\Big( \omega +\frac{\omega_0}{2}\Big) \Big] = \frac{1}{\omega_0} \frac{1}{\pi t} \sin \Big(\frac{\omega_0}{2} t \Big) e^{-j\frac{\omega_0}{2}t}sustituyendo en la ecuación principal,
-jtx_1(t) = \frac{1}{2\pi} e^{-j\omega_0 t} - \frac{1}{\omega_0} \frac{1}{\pi t} \sin \Big(\frac{\omega_0}{2} t \Big) e^{-j\frac{\omega_0}{2}t} + \frac{1}{\omega_0} \frac{1}{\pi t} \sin \Big(\frac{\omega_0}{2} t \Big) e^{j\frac{\omega_0}{2}t} - \frac{1}{2\pi} e^{j\omega_0 t}agrupando,
-jtx_1(t) = \frac{1}{2\pi}\Big( e^{-j\omega_0 t} -e^{j\omega_0 t}\Big) + \frac{1}{\omega_0 \pi t} \sin \Big(\frac{\omega_0}{2} t \Big)\Big(- e^{-j\frac{\omega_0}{2} t} +e^{j\frac{\omega_0}{2} t}\Big)para simplificar se divide ambos lados de la ecuación para -jt
x_1(t) = \frac{1}{\pi t}\Big( \frac{e^{j\omega_0 t}-e^{-j\omega_0 t} }{2j}\Big) - \frac{2}{\omega_0 \pi t^2 } \sin \Big(\frac{\omega_0}{2} t \Big)\Big(\frac{e^{j\frac{\omega_0}{2} t}- e^{-j\frac{\omega_0}{2} t}}{2j}\Big)que es la forma exponencial del seno y coseno
x_1(t) = \frac{1}{\pi t} \sin (\omega_0 t) - \frac{2}{\omega_0 \pi t^2 } \sin \Big(\frac{\omega_0}{2} t \Big) \sin \Big( \frac{\omega_0}{2} t \Big) x_1(t) = \frac{1}{\pi t}\sin (\omega_0 t) - \frac{2}{\omega_0 \pi t^2 }\sin^2 \Big(\frac{\omega_0}{2} t \Big) x_1(t) = \frac{\omega_0}{\pi}\frac{\sin (\omega_0 t)}{\omega_0 t} - \frac{\omega_0}{2\pi}\Bigg[\frac{\sin \Big(\frac{\omega_0}{2} t \Big)}{\frac{\omega_0}{2} t} \Bigg]^2ahora, considerando la gráfica de fase:
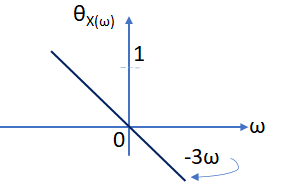
se tiene que,
x(t) = x_1(t-3) x(t) = \frac{\omega_0}{\pi}\frac{\sin (\omega_0 (t-3))}{\omega_0 (t-3)} - \frac{\omega_0}{2\pi}\Bigg[\frac{\sin \Big(\frac{\omega_0}{2} (t-3) \Big)}{\frac{\omega_0}{2} (t-3)}\Bigg]^2