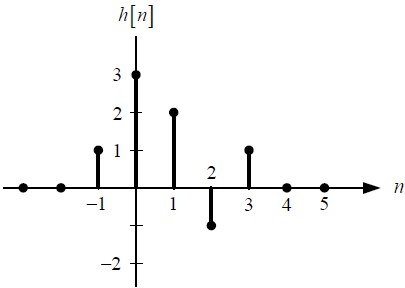3ra Evaluación I Término 2016-2017. 15/septiembre/2016 TELG1001
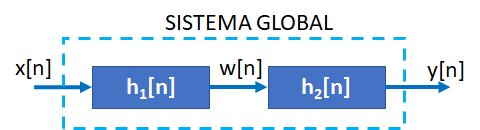
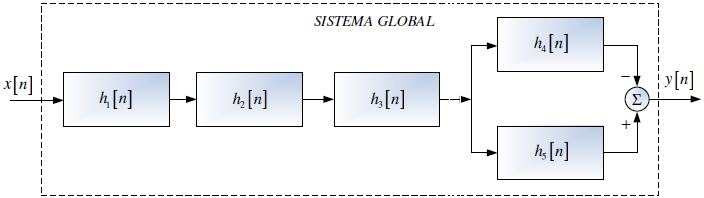
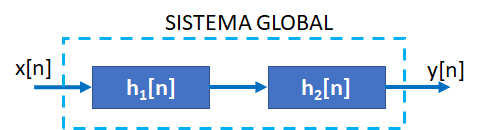
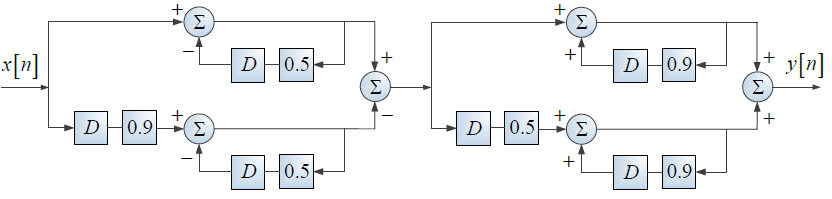
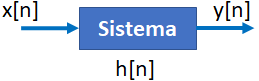
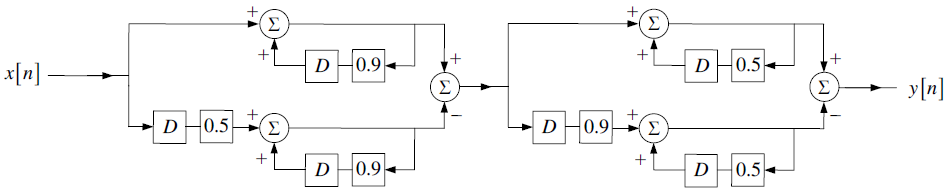
Tema 1. (26 puntos) Un sistema LTI-DT está integrado por la conexión en paralelo de dos subsistemas retroalimentados, tal como se muestra en la figura.
Determinar:
a. Las respuestas impulso de cada subsistema y del sistema completo, es decir h1[n], h2[n], h[n]
b. Comente sobre la estabilidad de cada subsistema y del sistema completo, justificando debidamente su respuesta.
c. La respuesta y[n] (expresada a la mínima expresión) frente a la entrada
x[n] = e^{-0.5n} \mu [n]Nota: Realizar el desarrollo en el Dominio del Tiempo Discreto o en el dominio de la Frecuencia Compleja z. Al final , la respuesta deberá ser la misma- Aquí se procederá a resolverlo utilizando las técnicas referidas al Dominio del tiempo discreto.
Coordinador: Tama Alberto