2.5.1 Método de la Secante – Ejemplo con Python

[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

---

1. Ejercicio

Referencia: Burden 2.1 ejemplo 1 p38

La ecuación mostrada tiene una raíz en el intervalo [1,2], ya que f(1) = -5 y f(2) = 14
Muestre los resultados parciales del algoritmo de la secante con una tolerancia de 0.0001

f(x) = x^3 + 4x^2 -10 =0

[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [función]
..

---

2. Desarrollo Analítico

siendo:

f(x) = x^3 + 4x^2 -10 =0 x_{i+1}= x_i - f(x_i)\frac{(x_{i-1} - x_i)}{f(x_{i-1}) - f(x_i)}

Se probará con valores iniciales que tienen el mismo signo f(x[i-1]), f(x[i]), que no se considera en el método cerrado de la posición falsa

itera = 0

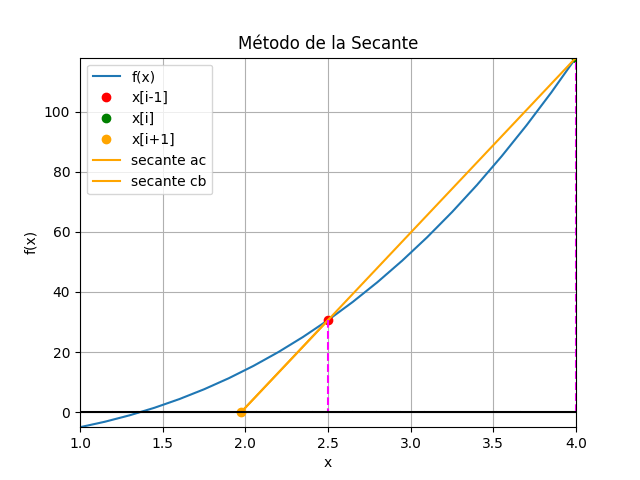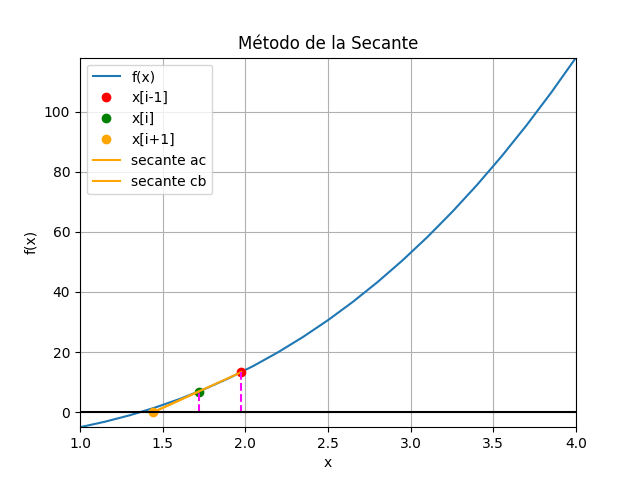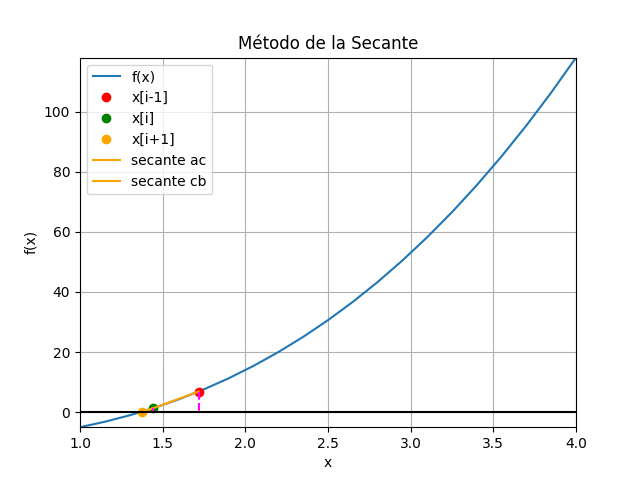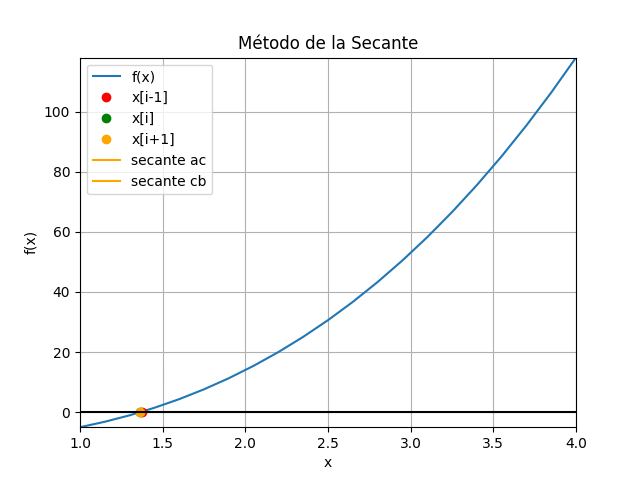
X_-1 = a =2.5,  X₀ =b=4, tolera = 0.001

f(2.5) = (2.5)^3 + 4(2.5)^2 -10 = 30.625 f(4) = (4)^3 + 4(4)^2 -10 =118 x_{1}= 4 - 118\frac{(2.5 - 4)}{(30.625 - 118)} = 1.9742 errado = |1.9742 - 4| = 2.02575

itera = 1

X₀ = 4,  X₁ = 1.9742

f(4) =118 f(1.9742) = ( 1.9742)^3 + 4( 1.9742)^2 -10 =13.2855 x_{2}= 1.9742 - (13.2855)\frac{(4 - 1.9742)}{(118 -13.2855)} =1.7172 errado = |1.7172 - 1.9742| = 0.2570

itera = 2

X₁ =1.9742, X₂ =1.7172

f(1.9742) = 13.2855 f(1.7172) = (1.7172)^3 + 4(1.7172)^2 -10 =6.8594 x_{3}= 1.7172 - (6.8594)\frac{(1.9742 - 1.7172)}{(6.8594 -13.2855)} = 1.4428 errado = | 1.4428- 1.7172| =0.2743

desarrollando una tabla con el algoritmo se tiene:

método de la Secante
i [ x[i-1], xi, x[i+1], f[i-1], fi ] tramo
0 [  2.5    4.       1.974249  30.625   118.      ] 2.0257510729613735
1 [  4.     1.974249 1.717233 118.       13.285584] 0.2570160557153698
2 [1.974249 1.717233 1.442883  13.285584  6.859484] 0.27434949602777015
3 [1.717233 1.442883 1.376796   6.859484  1.331607] 0.06608786561380797
4 [1.442883 1.376796 1.365656   1.331607  0.19207 ] 0.011139180030541596
5 [1.376796 1.365656 1.365232   0.19207   0.007041] 0.00042390961991034537
raiz en : 1.3652324200312267

[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

---

3. Algoritmo en Python

El algoritmo básico a usar es:

# Método de secante
import numpy as np

# INGRESO
fx = lambda x: x**3 + 4*x**2 - 10
a = 1
b = 4
tolera = 0.001
iteramax = 20
precision = 5

c = (a+b)/2 # probar dos puntos en un mismo lado de f(x)
# PROCEDIMIENTO
xi_1 = c
xi = b
itera = 0
tramo = np.abs(xi-xi_1)
print('i','[ x[i-1], xi, x[i+1], f[i-1], fi ]','tramo')
np.set_printoptions(precision)
while not(tramo<tolera or itera>iteramax):
    fi_1 = fx(xi_1)
    fi = fx(xi)
    xi1 = xi-fi*(xi_1 - xi)/(fi_1-fi)
    tramo = np.abs(xi1-xi)
    print(itera,np.array([xi_1,xi, xi1, fi_1,fi]),tramo)
    xi_1 = xi
    xi = xi1
    itera = itera + 1

respuesta = xi

# SALIDA
print('raiz: ',respuesta)

 

[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

---

4. Función en Python

Una función resumida, se recomienda realizar la validación de cambio de signo entre [a,b]

# Método de secante
import numpy as np

def secante_raiz(fx,a,b,tolera, iteramax=20,
                 vertabla=True, precision=6):
    '''fx en forma numérica lambda
    Los valores de [a,b] son seleccionados
    desde la gráfica de la función
    '''
    xi_1 = a
    xi = b
    itera = 0
    tramo = np.abs(xi-xi_1)
    if vertabla==True:
        print('método de la Secante')
        print('i','[ x[i-1], xi, x[i+1], f[i-1], fi ]','tramo')
        np.set_printoptions(precision)
    while not(tramo<tolera or itera>iteramax):
        fi_1 = fx(xi_1)
        fi = fx(xi)
        xi1 = xi-fi*(xi_1 - xi)/(fi_1-fi)
        tramo = np.abs(xi1-xi)
        if vertabla==True:
            print(itera,np.array([xi_1,xi,xi1,fi_1,fi]),tramo)
        xi_1 = xi
        xi = xi1
        itera = itera + 1
    if itera>=iteramax:
        xi = np.nan
        print('itera: ',itera,
              'No converge,se alcanzó el máximo de iteraciones')
    respuesta = xi
    
    return(respuesta)

# INGRESO
fx = lambda x: x**3 + 4*x**2 - 10
a = 1
b = 4
tolera = 0.001
c = (a+b)/2 # probar dos puntos en un mismo lado de f(x)

# PROCEDIMIENTO
respuesta = secante_raiz(fx,c,b,tolera,
                         vertabla=True,precision = 5)
# SALIDA
print('raíz en: ', respuesta)

Scipy.optimize.newton – Secante

El método de la secante se encuentra implementado en Scipy en la forma de algoritmo de newton, que al no proporcionar la función para la derivada de f(x), usa el método de la secante:

>>> import scipy.optimize as opt
>>> opt.newton(fx,xa, tol=tolera)
1.3652320383201266

https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.newton.html

---

[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]