Interpolación: [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Función ]
..
1. Ejercicio
Referencia: Rodríguez 6.1 p191, Chapra 18.3 p520
Unir n puntos en el plano usando un polinomios de interpolación se puede realizar con un polinomio de grado (n-1).
| xi | 0 | 0.2 | 0.3 | 0.4 |
|---|---|---|---|---|
| fi | 1 | 1.6 | 1.7 | 2.0 |
Por ejemplo, dados los 4 puntos en la tabla [xi,fi] se requiere generar un polinomio de grado 3 de la forma:
p(x) = a_0 x^3 + a_1 x^2 + a_2 x^1 + a_3Interpolación: [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Función ]
..
2. Desarrollo Analítico
Es posible generar un sistema de ecuaciones para p(x) haciendo que pase por cada uno de los puntos o coordenadas.
Por ejemplo si se toma el primer punto con xi=0 y fi=1 se establece la ecuación:
Note que ahora las incógnitas son los coeficientes ai. Luego se continúa con los otros puntos seleccionados hasta completar las ecuaciones necesarias para el grado del polinomio seleccionado.
a_0 (0.0)^3 + a_1 (0.0)^2 + a_2 (0.0)^1 + a_3 = 1.0 a_0 (0.2)^3 + a_1 (0.2)^2 + a_2 (0.2)^1 + a_3 = 1.6 a_0 (0.3)^3 + a_1 (0.3)^2 + a_2 (0.3)^1 + a_3 = 1.7 a_0 (0.4)^3 + a_1 (0.4)^2 + a_2 (0.4)^1 + a_3 = 2.0El sistema obtenido se resuelve con alguno de los métodos conocidos para la Solución a sistemas de ecuaciones, que requieren escribir las ecuaciones en la forma de matriz A y vector B, desarrollar la matriz aumentada, pivotear por filas, etc.
\begin{pmatrix} 0.0^3 & 0.0^2 & 0.0^1 & 1 \\ 0.2^3 & 0.2^2 & 0.2^1 & 1 \\ 0.3^3 & 0.3^2 & 0.3^1 & 1 \\ 0.4^3 & 0.4^2 & 0.4^1 & 1 \end{pmatrix} . \begin{pmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \end{pmatrix} = \begin{pmatrix} 1.0 \\ 1.6 \\ 1.7 \\ 2.0 \end{pmatrix}La matriz A también se conoce como Matriz Vandermonde D, que se construye observando que los coeficientes se elevan al exponente referenciado al índice columna pero de derecha a izquierda. La última columna tiene valores 1 por tener como coeficiente el valor de xi0.
Para enfocarnos en la interpolación, en la solución se propone usar un algoritmo o función en Python, obteniendo el siguiente resultado:
los coeficientes del polinomio: [ 41.66666667 -27.5 6.83333333 1. ]
a partir del cual que se construye el polinomio con los valores obtenidos.
Polinomio de interpolación p(x): 41.6666666666667*x**3 - 27.5*x**2 + 6.83333333333333*x + 1.0
que re-escrito es,
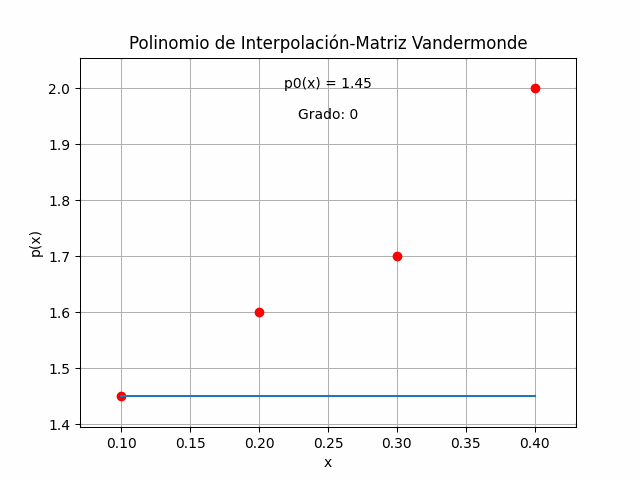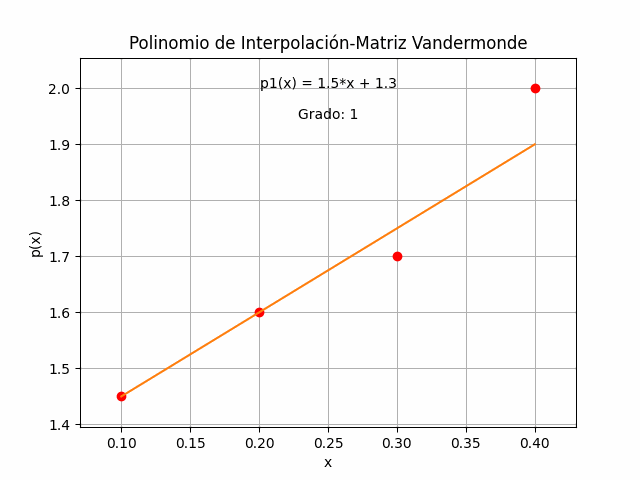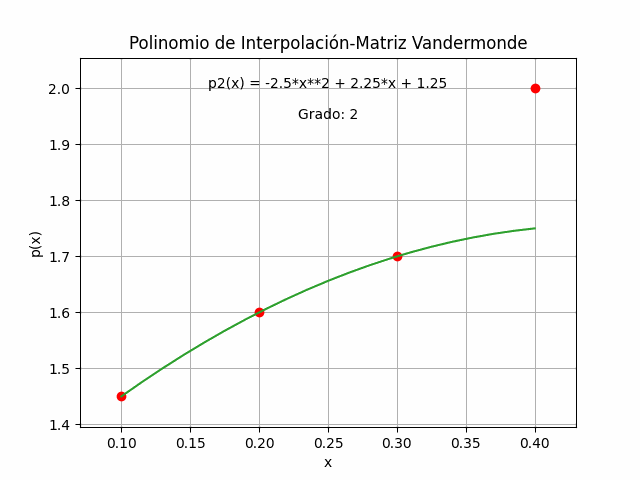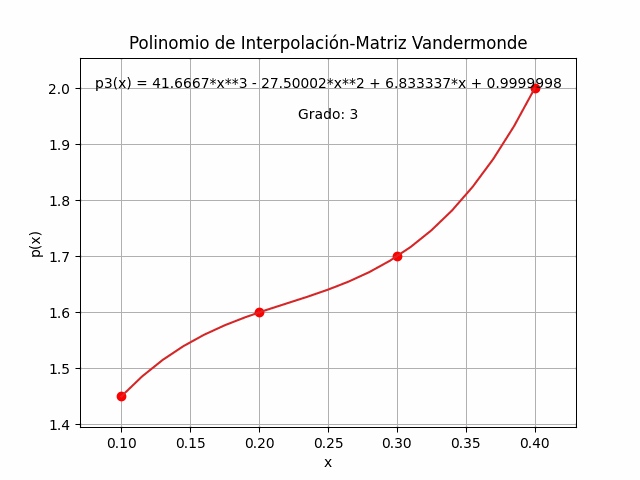
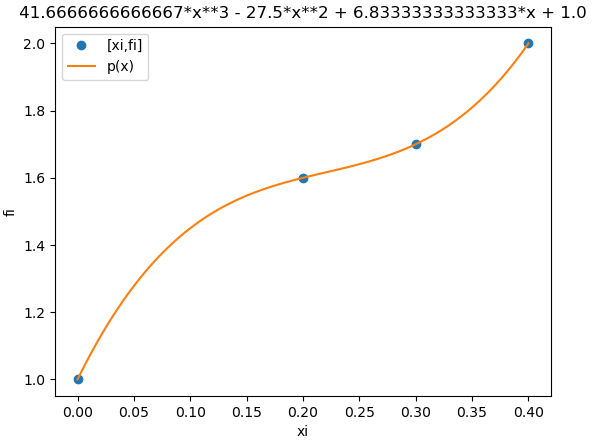
p(x) = 41.6666 x^3 - 27.5 x^2 + 6.8333 x + 1Se realiza la gráfica de p(x) dentro del intervalo de los datos del ejercicio y se obtiene la línea contínua que pasa por cada uno de los puntos.
Interpolación: [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Función ]
..
3. Algoritmo en Python
Para desarrollar el ejercicio, se realiza un bloque para construir la matriz A y vector B, usando los vectores que representan los puntos de muestra de la función o experimento.
xi = [0,0.2,0.3,0.4] fi = [1,1.6,1.7,2.0]
Observe que en éste caso los datos se dan en forma de lista y se deben convertir hacia arreglos.
La matriz A o Matriz Vandermonde D, se construye observando que los coeficientes del vector xi se elevan al exponente referenciado al índice columna pero de derecha a izquierda.
Construir el polinomio consiste en resolver el sistema de ecuaciones indicado en la sección anterior. Para simplificar la solución del sistema, se usa Numpy, que entrega el vector solución que representan los coeficientes del polinomio de interpolación.
Para construir la expresión del polinomio, se usa la forma simbólica con Sympy, de forma semejante a la usada para construir el polinomio de Taylor.
Para mostrar el polinomio de una manera más fácil de interpretar se usa la instrucción sym.pprint(), usada al final del algoritmo.
# El polinomio de interpolación import numpy as np import sympy as sym # INGRESO xi = [0,0.2,0.3,0.4] fi = [1,1.6,1.7,2.0] # PROCEDIMIENTO # Convierte a arreglos numpy xi = np.array(xi,dtype=float) fi = np.array(fi,dtype=float) B = fi n = len(xi) # Matriz Vandermonde D D = np.zeros(shape=(n,n),dtype=float) for i in range(0,n,1): for j in range(0,n,1): potencia = (n-1)-j # Derecha a izquierda D[i,j] = xi[i]**potencia # Aplicar métodos Unidad03. Tarea # Resuelve sistema de ecuaciones A.X=B coeficiente = np.linalg.solve(D,B) # Polinomio en forma simbólica x = sym.Symbol('x') polinomio = 0 for i in range(0,n,1): potencia = (n-1)-i # Derecha a izquierda termino = coeficiente[i]*(x**potencia) polinomio = polinomio + termino # SALIDA print('Matriz Vandermonde: ') print(D) print('los coeficientes del polinomio: ') print(coeficiente) print('Polinomio de interpolación: ') print(polinomio) print('\n formato pprint') sym.pprint(polinomio)
con lo que se obtiene el siguiente resultado:
Matriz Vandermonde:
[[0. 0. 0. 1. ]
[0.008 0.04 0.2 1. ]
[0.027 0.09 0.3 1. ]
[0.064 0.16 0.4 1. ]]
los coeficientes del polinomio:
[ 41.66666667 -27.5 6.83333333 1. ]
Polinomio de interpolación:
41.6666666666667*x**3 - 27.5*x**2 + 6.83333333333333*x + 1.0
formato pprint
3 2
41.6666666666667*x - 27.5*x + 6.83333333333333*x + 1.0
Gráfica del polinomio
Para facilitar la evaluación numérica del polinomio, se convierte el polinomio a la forma Lambda px. La gráfica se realiza con un número de muestras suficientes para suavizar la curva dentro del intervalo [a,b], por ejemplo 21, con lo que se comprueba que la curva pase por todos los puntos de la tabla xi,fi dados en el ejercicio.
Instrucciones adicionales al algoritmo para la gráfica:
# GRAFICA import matplotlib.pyplot as plt # Polinomio a forma Lambda x: # para evaluación con vectores de datos xin # muestras = tramos+1 muestras = 21 px = sym.lambdify(x,polinomio) a = np.min(xi) b = np.max(xi) xin = np.linspace(a,b,muestras) yin = px(xin) # Usando evaluación simbólica ##yin = np.zeros(muestras,dtype=float) ##for j in range(0,muestras,1): ## yin[j] = polinomio.subs(x,xin[j]) plt.plot(xi,fi,'o', label='[xi,fi]') plt.plot(xin,yin, label='p(x)') plt.xlabel('xi') plt.ylabel('fi') plt.legend() plt.title(polinomio) plt.show()
Interpolación: [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Función ]
..
4. Función en Scipy
>>> import scipy as sp >>> xi = [0,0.2,0.3,0.4] >>> fi = [1,1.6,1.7,2.0] >>> sp.interpolate.lagrange(xi,fi) poly1d([ 41.66666667, -27.5 , 6.83333333, 1. ]) >>>
Interpolación: [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Función ]