[ Simpson 3/8 ] [ Ejercicio ] [Algoritmo /función Python]
Regla de Simpson 3/8
Referencia: Chapra 21.2.1 p.631, Burden 4.2 p147, Rodríguez 7.1.8 p288
I\cong \frac{3h}{8}[f(x_0)+3f(x_1) +3 f(x_2)+f(x_3)]Es el resultado cuando para el integral se utiliza el resultado de una interpolación con polinomio de tercer grado.
I = \int_a^b f(x) \delta x I \cong \int_a^b f_3 (x) \delta xAl desarrollar la fórmula de la Regla de Simpson de 3/8 para un segmento con tres tramos con distancia h:
I\cong \frac{3h}{8}[f(x_0)+3f(x_1) +3 f(x_2)+f(x_3)]siendo el tramo de un segmento [a,b]
h=\frac{b-a}{3}Error de Truncamiento
error_{truncamiento} = -\frac{3}{80} h^5 f^{(4)} (z)donde z se encuentra entre [a,b]
[ Simpson 3/8 ] [ Ejercicio ] [Algoritmo /función Python]
Ejercicio
Para integrar la función en el intervalo [1,3] con 6, 18, 24 y 72 tramos,
f(x)= \sqrt {(x)} \sin(x) 1 \leq x \leq 3Para el ejercicio planteado en la regla de trapecio, usando seis tramos, se aplica el método cada tres tramos.
f(x)= \sqrt {(x)} \sin(x) 1 \leq x \leq 3tramos = 6
h = \frac{3-1}{6} = \frac{1}{3} I\cong \frac{3}{8}\Big(\frac{1}{3}\Big)[f(1)+3f\Big(1+\frac{1}{3}\Big) +3f\Big(1+\frac{2}{3}\Big) + f(2)] + + \frac{3}{8}\Big(\frac{1}{3}\Big)[f(2)+3f\Big(2+\frac{1}{3}\Big) +3f\Big(2+\frac{2}{3}\Big)+ f(3)] f(1)= \sqrt {(1)} \sin(1) = 0.8414 f(4/3)= \sqrt {(4/3)} \sin(4/3) = 1.1222 f(5/3)= \sqrt {(5/3)} \sin(5/3) = 1.2850 f(2)= \sqrt {(2)} \sin(2) = 1.2859 f(7/3)= \sqrt {(7/3)} \sin(7/3) = 1.1045 f(8/3)= \sqrt {(8/3)} \sin(8/3) = 0.7467 f(3)= \sqrt {(3)} \sin(3) = 0.2444 I\cong \frac{3}{24}[0.8414+3(1.1222)+3(1.2850)+1.2859] + \frac{3}{24}[1.2859+3(1.1045)+3(0.7467)+0.2444] I\cong 2.0542las muestras para el ejercicio son:
>>> import numpy as np
>>> fx = lambda x: np.sqrt(x)*np.sin(x)
>>> xi = [1, 1+1/3, 1+2/3, 2, 1+4/3, 1+5/3, 3]
>>> fx(xi)
array([0.84147098, 1.12229722, 1.28506615, 1.28594075,
1.10453193, 0.74672307, 0.24442702]
>>> I1=(3/8)*(1/3)*(fx(1)+3*fx(1+1/3)+3*fx(1+2/3)+fx(2))
>>> I2=(3/8)*(1/3)*(fx(2)+3*fx(1+4/3)+3*fx(1+5/3)+fx(3))
>>> I1+I2
2.0542043270535757
>>>
[ Simpson 3/8 ] [ Ejercicio ] [Algoritmo /función Python]
Algoritmo en Python
A partir del algoritmo para Simpson de 1/3, se realizan modificaciones para obtener el algoritmo de Simpson de 3/8:
Resultados de algoritmo
tramos: 6 Integral con Simpson 3/8: 2.0542043270535757
Caso: f(x) es una expresión matemática
# Integración Simpson 3/8 import numpy as np import matplotlib.pyplot as plt def integrasimpson38(fx,a,b,tramos): ''' integral con método de Simpson 3/8 tramos debe ser múltiplo de 3 ''' # Validar cantidad de tramos múltiplo de 3 esmult3 = tramos%3 if esmult3 != 0: suma = 'tramos debe ser múltiplo de 3' # Regla de Simpson 3/8 if esmult3 == 0: h = (b-a)/tramos xi = a suma = 0 for i in range(0,tramos,3): unS38 = (3/8)*h*(fx(xi)+3*fx(xi+h)+3*fx(xi+2*h)+fx(xi+3*h)) suma = suma + unS38 xi = xi + 3*h return(suma) # PROGRAMA ----------------- # INGRESO fx = lambda x: np.sqrt(x)*np.sin(x) # intervalo de integración a = 1 b = 3 tramos = 6 # PROCEDIMIENTO Area = integrasimpson38(fx,a,b,tramos) # SALIDA print('tramos: ',tramos) print('Integral con Simpson 3/8: ',Area) if type(Area)==str: print(' Revisar errores...')
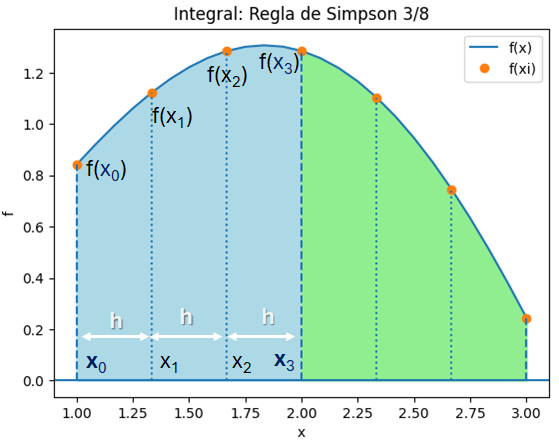
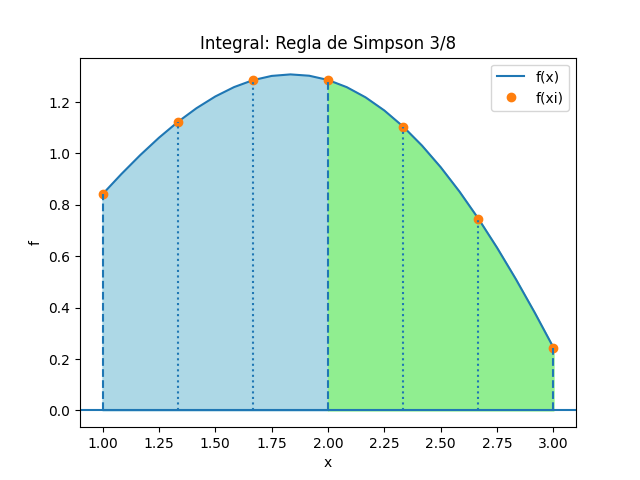
Gráfica
Se puede observar mejor lo expresado usando la gráfica para observar los tramos, muestras, por segmento.
Se puede cambiar el número de tramos en el algoritmo anterior, considerando que deben ser múltiplo de 3.
 Instrucciones en Python adicionales al algoritmo anterior
Instrucciones en Python adicionales al algoritmo anterior
# GRAFICA # fx muestras por tramo muestras = tramos + 1 xi = np.linspace(a,b,muestras) fi = fx(xi) fi0 = np.zeros(muestras) # linea base # fx suave aumentando muestras muestrasfxSuave = 4*tramos + 1 xk = np.linspace(a,b,muestrasfxSuave) fk = fx(xk) # Relleno for i in range(0,muestras-2,3): relleno = 'lightgreen' if (i/3)%2==0: # i/3 multiplo 2 relleno ='lightblue' xktramo = xk[i*4:(i+3)*4+1] fktramo = fk[i*4:(i+3)*4+1] plt.fill_between(xktramo,fktramo,fktramo*0,color=relleno) # Funcion f(x) plt.plot(xk,fk, label='f(x)') plt.plot(xi,fi,'o', label='f(xi)') # Divisiones entre Simpson 3/8 for i in range(0,muestras,1): tipolinea = 'dotted' if i%3==0: # multiplo de 3 tipolinea = 'dashed' plt.vlines(xi[i],fi0[i],fi[i], linestyle=tipolinea) plt.axhline(0) plt.xlabel('x') plt.ylabel('f') plt.title('Integral: Regla de Simpson 3/8') plt.legend() plt.show()
Caso: x[i], f[i] son muestras
xi = [1. , 1.33333333, 1.66666667, 2. ,
2.33333333, 2.66666667, 3. ]
fi = [0.84147098, 1.12229722, 1.28506615, 1.28594075,
1.10453193, 0.74672307, 0.24442702]
tolera = 1e-7
Instrucciones en Python
# Integración Simpson 1/3 # Usando una muestras xi,fi import numpy as np import matplotlib.pyplot as plt def integrasimpson38_fi(xi,fi,tolera = 1e-10): ''' sobre muestras de fi para cada xi integral con método de Simpson 3/8 respuesta es np.nan para tramos desiguales, no hay suficientes puntos. ''' n = len(xi) i = 0 suma = 0 while not(i>=(n-3)): h = xi[i+1]-xi[i] h1 = (xi[i+2]-xi[i+1]) h2 = (xi[i+3]-xi[i+2]) dh = abs(h-h1)+abs(h-h2) if dh<tolera:# tramos iguales unS38 = fi[i]+3*fi[i+1]+3*fi[i+2]+fi[i+3] unS38 = (3/8)*h*unS38 suma = suma + unS38 else: # tramos desiguales suma = 'tramos desiguales' i = i + 3 if (i+1)<n: # incompleto, tramos por calcular suma = 'tramos incompletos, faltan ' suma = suma +str(n-(i+1))+' tramos' return(suma) # PROGRAMA ----------------- # INGRESO xi = [1. , 1.33333333, 1.66666667, 2. , 2.33333333, 2.66666667, 3. ] fi = [0.84147098, 1.12229722, 1.28506615, 1.28594075, 1.10453193, 0.74672307, 0.24442702] tolera = 1e-7 # PROCEDIMIENTO n = len(xi)-1 Area = integrasimpson38_fi(xi,fi,tolera) # SALIDA print('tramos: ',n) print('Integral con Simpson 3/8: ',Area) if type(Area)==str: print(' Revisar errores')
[ Simpson 3/8 ] [ Ejercicio ] [Algoritmo /función Python]