Referencia: Chapra 21.2.1 p631 pdf655, Burden 4.2 p192 pdf202, Rodriguez 7.1.4 p281
Es el resultado cuando se realiza una interpolación con polinomio de segundo grado.
Usando un polinomio de Lagrange de segundo grado:
I = \int_{x_0}^{x_2} \bigg[ \frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} f(x_0) + + \frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)} f(x_1) + + \frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} f(x_2) \bigg] \delta xque tiene como resultado para un solo tramo:
I\cong \frac{h}{3}[f(x_0)+4f(x_1) + f(x_2)]siendo
h=\frac{b-a}{2}Error de truncamiento
la cota del error de truncamiento se estima como O(h5)
error_{trunca} = -\frac{h^5}{90} f^{(4)}(z)para un valor de z entre [a,b]
para cuantificar el valor, se puede usar la diferencia finita Δ4f, pues con la derivada sería muy laborioso.
Ejercicio
Para el ejercicio planteado en la regla de trapecio, usando cuatro tramos, se aplica el método cada dos tramos.
f(x)= \sqrt {(x)} \sin(x) 1 \leq x \leq 3tramos = 4
h = \frac{3-1}{4} = 0.5 I\cong \frac{0.5}{3}[f(1)+4f(1.5) + f(2)] + + \frac{0.5}{3}[f(2)+4f(2.5) + f(3)] I\cong 2.054Note que al usar Simpson 1/3 con 4 tramos el resultado tiene los 2 primeros decimales iguales a usar Trapecio con 16 tramos.
tramos: 4 Integral: 2.0549261957703937 >>>
Algoritmo en Python
Del ejercicio con trapecios, se repite el ejercicio con n tramos; usando dos tramos o tres puntos por cada iteración. Cada iteración se procesa avanzando dos puntos xi. Ejemplo:
tramos: 8 Integral: 2.05363501328 >>>
A continuación se presentan dos formas de algoritmos que entregan los mismos resultados. Como tarea puede revisar la diferencia de tiempos de ejecución de cada uno.
Algoritmo conceptual
Se realiza mediante la aplicación directa de la forma conceptual de la fórmula para cada segmento conformado de dos tramos.
# Integración: Regla Simpson 1/3 import numpy as np import matplotlib.pyplot as plt # INGRESO: fx = lambda x: np.sqrt(x)*np.sin(x) # intervalo de integración a = 1 b = 3 tramos = 8 # PROCEDIMIENTO # Tarea: validar tramos par # Regla de Simpson 1/3 h = (b-a)/tramos xi = a area = 0 for i in range(0,tramos,2): deltaA = (h/3)*(fx(xi)+4*fx(xi+h)+fx(xi+2*h)) area = area + deltaA xi = xi + 2*h # SALIDA print('tramos:', tramos) print('Integral: ', area)
Algoritmo con varios segmentos y h constante
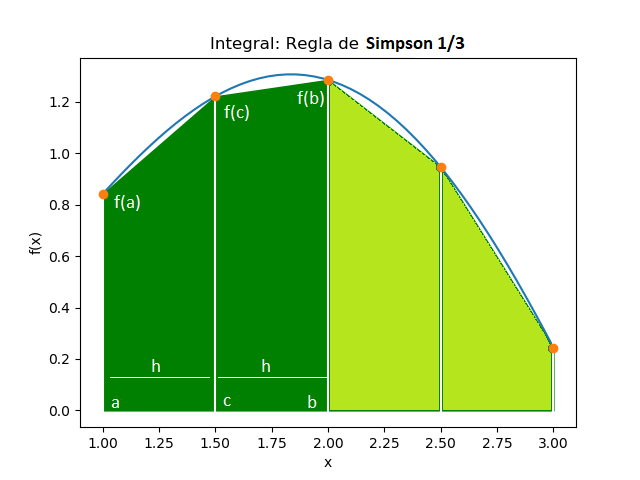
Usado cuando el intervalo a integrar tiene varios segmentos, cada segmento tiene dos tramos. Ejemplo para dos segmentos, cuatro tramos, semejante al usado en la gráfica. La simplificación es válida si h es constante.
I\cong \frac{h}{3}[f(x_0)+4f(x_1) + f(x_2)] + + \frac{h}{3}[f(x_2)+4f(x_3) + f(x_4)]tomando factor común h/3
I\cong \frac{h}{3}[f(x_0)+4f(x_1) + 2f(x_2) + +4f(x_3) + f(x_4)]# Integración: Regla Simpson 1/3 # Validar cantidad de tramos pares import numpy as np import matplotlib.pyplot as plt # INGRESO fx = lambda x: np.sqrt(x)*np.sin(x) # intervalo de integración a = 1 b = 3 tramos = 8 # Validar cantidad de tramos pares esimpar = tramos%2 while (esimpar == 1): tramos = int(input('tramos es par: ')) esimpar = tramos%2 # PROCEDIMIENTO # Regla de Simpson 1/3, varios tramos h = (b-a)/tramos xi = a # segmento por cada dos tramos suma = fx(xi) for i in range(0,tramos-2,2): xi = xi + h suma = suma + 4*fx(xi) xi = xi + h suma = suma + 2*fx(xi) # último segmento xi = xi + h suma = suma + 4*fx(xi) suma = suma + fx(b) area = (h/3)*suma # SALIDA print('tramos: ', tramos) print('Integral: ', area)
Gráfica
Se puede observar mejor lo expresado usando la gráfica, en la que cada segmento se destaca con diferente color.
Tarea: realizar la gráfica de la función y las áreas bajo las curvas
Algoritmo con muestras
Cuando se integra sobre muestras dadas por los vectores xi, fi. Se revisa que los tramos entre muestras sean iguales para un Simpson 1/3 y que existan suficientes puntos para completar el integral.
# Integración Simpson 1/3 # Usando una muestras xi,fi import numpy as np import matplotlib.pyplot as plt def integrasimpson13_fi(xi,fi,tolera = 1e-10): ''' sobre muestras de fi para cada xi integral con método de Simpson 1/3 respuesta es np.nan para tramos desiguales, no hay suficientes puntos. ''' n = len(xi) i = 0 suma = 0 while not(i>=(n-2)): h = xi[i+1]-xi[i] dh = abs(h - (xi[i+2]-xi[i+1])) if dh<tolera:# tramos iguales unS13 = (h/3)*(fi[i]+4*fi[i+1]+fi[i+2]) suma = suma + unS13 else: # tramos desiguales suma = 'tramos desiguales' i = i + 2 if i<(n-1): # incompleto, faltan tramos por calcular suma = 'tramos incompletos, faltan ' suma = suma ++str((n-1)-i)+' tramos' return(suma) # PROGRAMA ----------------- # INGRESO xi = [1. , 1.5, 2. , 2.5, 3.] fi = [0.84147098, 1.22167687, 1.28594075, 0.94626755, 0.24442702] # PROCEDIMIENTO Area = integrasimpson13_fi(xi,fi) # SALIDA print('tramos: ',len(xi)-1) print('Integral con Simpson 1/3: ',Area) if type(Area)==str: print(' Revisar errores...')
resultados
tramos: 4 Integral con Simpson 1/3: 2.0549261966666665 >>>