Ejercicio: 1Eva_IIIT2007_T2 Función Cobb-Douglas
[ a1 interpola filas ] [a2 interpola punto Y] [ b1 interpola columnas ] [ b2 raíz Newton-Raphson] [ Algoritmo ]
..
literal a.1 Interpola tabla por filas
Se usa la tabla para plantear los polinomios usando los datos de cada fila. Se evalúa el polinomio con el valor de K=25 (en miles) para completar los datos de la columna K=25
| L\K (miles $) |
10 |
20 |
25 |
30 |
40 |
| 0 |
0 |
0 |
|
0 |
0 |
| 10 |
11.0000 |
13.0813 |
|
14.4768 |
15.5563 |
| 20 |
18.4997 |
22.0000 |
|
24.3470 |
26.1626 |
| 25 |
|
|
Y |
|
|
| 30 |
25.0746 |
29.8189 |
|
33.0000 |
35.4608 |
Para la fila L=0 no es necesario realizar un polinomio, pues se observa que para 0 trabajadores la producción es nula, no existe producción p(K)=0 y pK(25)=0.
Para la fila L=10, se disponen de 4 puntos, por lo que se plantea un polinomio de grado 3:
P_{L10}(K) = 11\frac{(K-20)(K-30)(K-40)}{(10-20)(10-30)(10-40)} +
+ 13.0813\frac{(K-10)(K-30)(K-40)}{(20-10)(20-30)(20-40)} +
+ 14.4768\frac{(K-10)(K-20)(K-40)}{(30-10)(30-20)(30-40)} +
+ 15.5563\frac{(k-10)(k-20)(k-30)}{(40-10)(40-20)(40-30)}
Con el algoritmo se simplifica la expresión:
P_{L10}(K) =0.0000616335 K^3 - 0.0071269*K^2 + 0.378796 K + 7.8630
Se evalúa el polinomio con K=25
P_{L10}(K) =0.0000616335 (25)^3 - 0.0071269*(25)^2 + 0.378796 (25) + 7.8630
P_{L10}(25) = 13.84166
Se observan los resultados encontrados en la primera gráfica:
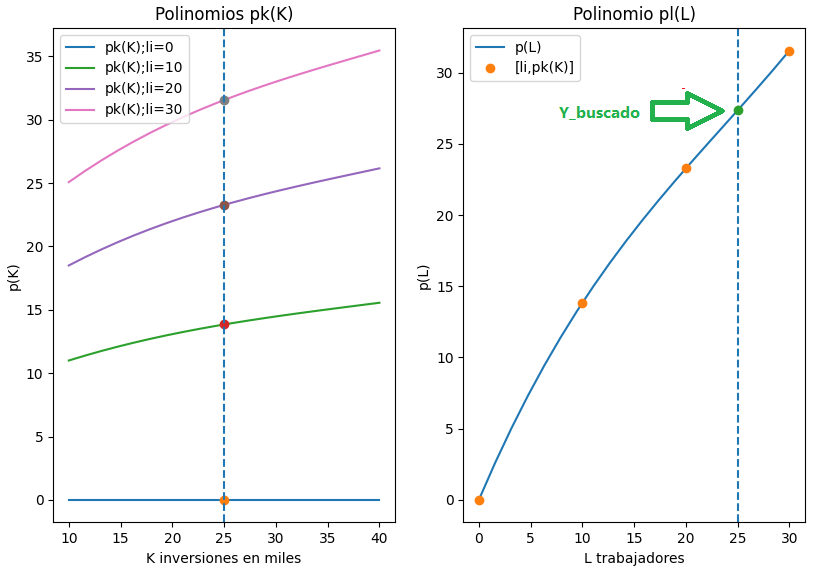
Se continua el ejercicio usando los algoritmos para encontrar los polinomios de Lagrange obteniendo:
**** literal a:
Polinomio de Lagrange por fila de L
fila: 0 , li[fila]: 0 , polinomio pk :
0
pk[25]: 0
___
fila: 1 , li[fila]: 10 , polinomio pk :
3 2
6.16333333333342e-5*K - 0.00712699999999999*K + 0.378796666666668*K + 7.86309999999999
pk[25]: 13.8416625000000
___
fila: 2 , li[fila]: 20 , polinomio pk :
3 2
0.000103649999999999*K - 0.0119855*K + 0.637039999999995*K + 13.2242
pk[25]: 23.2787937499999
___
fila: 3 , li[fila]: 30 , polinomio pk :
3 2
0.00014048333333333*K - 0.0162449999999998*K + 0.863441666666663*K + 17.9242
pk[25]: 31.5521687500000
___
Datos para el polinomio de L
li:
[ 0 10 20 30]
k_buscado:
[0, 13.8416625000000, 23.2787937499999, 31.5521687500000]
[ a1 interpola filas ] [a2 interpola punto Y] [ b1 interpola columnas ] [ b2 raíz Newton-Raphson] [ Algoritmo ]
..
literal a.2 Interpola un punto en Y con K=25
Con los datos obtenidos se genera el siguiente polinomio P(L), que corresponde a la parte derecha de la gráfica mostrada.
P_{k=25}(L) = 0\frac{(L-10)(L-20)(L-30)}{(0-10)(0-20)(0-30)} +
+ 13.84166\frac{(L-0)(L-20)(L-30)}{(10-0)(10-20)(10-30)} +
+ 23.27879\frac{(L-0)(L-10)(L-30)}{(20-0)(20-10)(20-30)} +
+ 31.55216\frac{(L-0)(L-10)(L-20)}{(30-0)(30-10)(30-20)}
simplificando con el algoritmo se tiene:
P_{k=25}(L) = 00.00054012 L^3 - 0.038226 L^2 + 1.71241 L
evaluando el polinomio con L=25
P_{k=25}(L) = 00.00054012 (25)^3 - 0.038226 (25)^2 + 1.71241 (25)
P_{k=25}(L) = 27.358402
Con los datos obtenidos se realiza la gráfica en 3D marcando los puntos calculados con los polinomios.
![Cobb Douglas Y[L,K]](http://blog.espol.edu.ec/analisisnumerico/files/2017/11/CobbDouglas01.png)
[ a1 interpola filas ] [a2 interpola punto Y] [ b1 interpola columnas ] [ b2 raíz Newton-Raphson] [ Algoritmo ]
..
literal b.1 Interpola tabla por columnas
| L\K (miles $) |
10 |
20 |
K=? |
30 |
40 |
| 0 |
0 |
0 |
|
0 |
0 |
| 10 |
11.0000 |
13.0813 |
|
14.4768 |
15.5563 |
| 20 |
18.4997 |
22.0000 |
|
24.3470 |
26.1626 |
| 25 |
|
|
Y=30 |
|
|
| 30 |
25.0746 |
29.8189 |
|
33.0000 |
35.4608 |
Se repite el ejercicio del literal a, con el mismo algoritmo para no rescribir todo por las filas por columnas. En el algoritmo se intercambian las filas por columnas y se transpone la matriz.
# INGRESO
...
# Se intercambian los valores de fila columna para repetir el algoritmo
# obteniendo Y(L=25,k)
M = np.transpose(M)
kj = [0, 10, 20, 30]
li = [10, 20, 30, 40]
l_busca = 25 # trabajadores
k_busca = 25 # inversión en miles de $
Se ajustan las etiquetas de las gráficas y se obtiene el polinomio a usar, que es la producción Y(k) para un capital K dado:
Y(K) = P_{L=25}(K) =
0.000121812500000016*K**3 - 0.0140857812500013*K**2 +
0.748676562500027*K + 15.5417812499999
Y(K) = 0.00012181 K^3 - 0.014085 K^2 + 0.74867 K + 15.54178
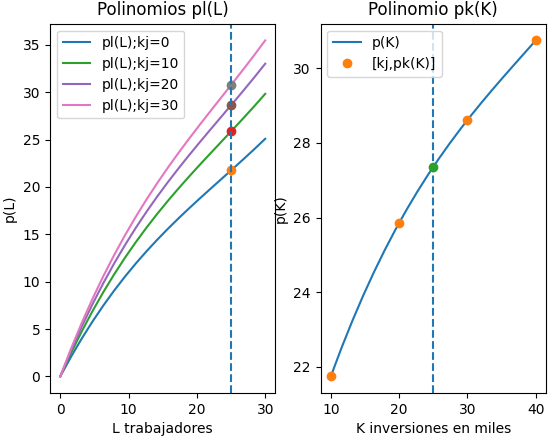
[ a1 interpola filas ] [a2 interpola punto Y] [ b1 interpola columnas ] [ b2 raíz Newton-Raphson] [ Algoritmo ]
..
literal b.2 raíz con Newton-Raphson
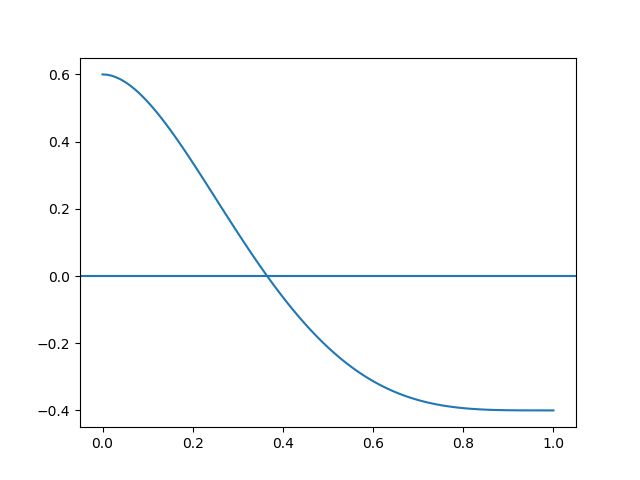
Para el algoritmo de Newton- Raphson, el ejercicio se plantea igualando el polinomio al valor buscado de producción Y=30. Se escribe luego la expresión en como f(x)=0 y f'(x):.
0.00012181 K^3 - 0.014085 K^2 + 0.74867 K + 15.54178 = 30
f(K) = 0.00012181 K^3 - 0.014085 K^2 + 0.74867 K + 15.54178 - 30
f'(K) = 0.0001218(3) K^2 - 0.014085(2) K+ 0.74867
f'(K) = 0.00036543 K^2 - 0.02817 K+ 0.74867
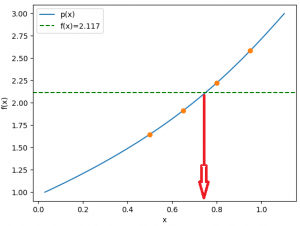
Usando la gráfica se inicia con K0=30, por ser el valor mas cercano de los puntos conocidos a Y=30, se obtienen los siguientes resultados:
itera = 0
f(30) = 0.00012181 (30)^3 - 0.014085 (30)^2 + 0.74867 (30) +
+ 15.54178 - 30 = -1.3862
f'(30) = 0.00036543 (30)^2 - 0.02817 (30)+ 0.74867 = 0.2325
K_{1} = 30 -\frac{-1.3862}{0.2325} = 35.963
errado = |35.963 -30| = 5.963
itera = 1
f(35.963) = 0.00012181 (35.963)^3 - 0.014085 (35.963)^2 +
+ 0.74867 (35.963) + 15.54178 - 30 = -0.0854
f'(35.963) = 0.00036543 (35.963)^2 - 0.02817 (35.963)
+ 0.74867 = 0.2082
K_{2} = 35.963 -\frac{-0.0854}{0.2082} = 36.3734
errado = |36.3734 -35.963| = 0.4104
itera = 2
f( 36.3734) = 0.00012181 ( 36.3734)^3 - 0.014085 ( 36.3734)^2 +
+ 0.74867 ( 36.3734) + 15.54178 - 30 = -0.00016955
f'( 36.3734) = 0.00036543 ( 36.3734)^2 - 0.02817 ( 36.3734)+
+ 0.74867 = 0.20751
K_{3} = 36.3734 -\frac{-0.00016955}{0.20751} = 36.374
errado = |36.374 - 36.3734| = 0.00081705
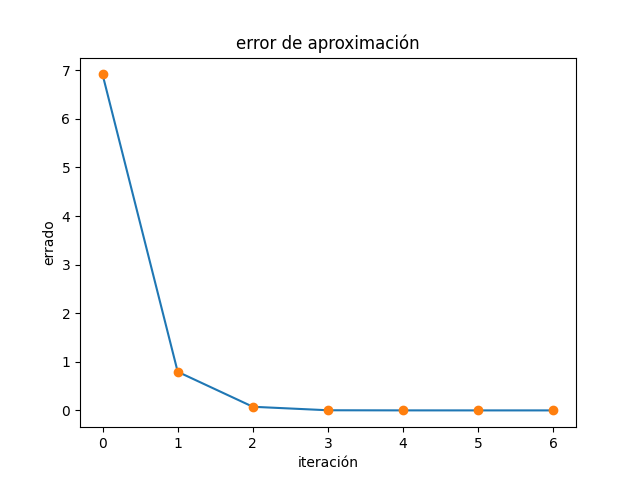
Se observa que el error disminuye en cada iteración, por lo que el método converge.
Se sigue con las iteraciones usando el algoritmo:
método de Newton-Raphson
i ['xi', 'fi', 'dfi', 'xnuevo', 'tramo']
0 [30. -1.3862 0.2325 35.963 5.963 ]
1 [35.963 -0.0854 0.2082 36.3734 0.4104]
2 [ 3.6373e+01 -1.6955e-04 2.0751e-01 3.6374e+01 8.1705e-04]
3 [ 3.6374e+01 -3.8858e-08 2.0751e-01 3.6374e+01 1.8726e-07]
raíz en: 36.3742052500759
Se encuentra la raíz en 36.3741, que corresponde a una inversión K un poco mas de 36 mil dólares para una producción Y de 30 mil unidades.
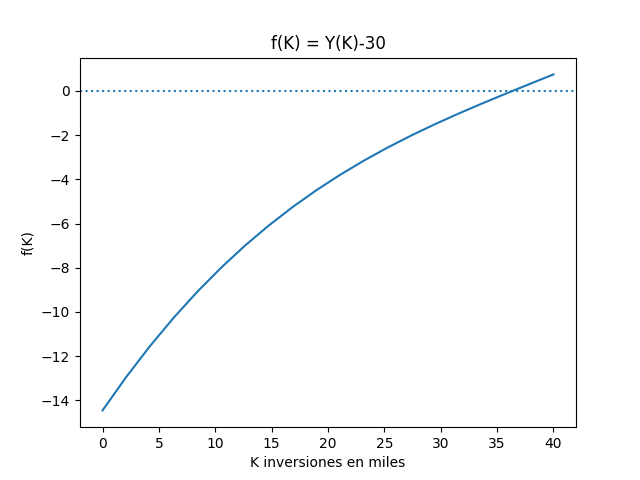 [ a1 interpola filas ] [a2 interpola punto Y] [ b1 interpola columnas ] [ b2 raíz Newton-Raphson] [ Algoritmo ]
[ a1 interpola filas ] [a2 interpola punto Y] [ b1 interpola columnas ] [ b2 raíz Newton-Raphson] [ Algoritmo ]
..
Instrucciones en Python. literal a
#1Eva_IIIT2007_T2 Función Cobb-Douglas
# Interpolacion de Lagrange
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
def interpola_lagrange(xi,yi):
'''
Interpolación con método de Lagrange
resultado: polinomio en forma simbólica
'''
# PROCEDIMIENTO
n = len(xi)
x=sym.Symbol('x')
# Polinomio
polinomio = 0*x # inicializa con cero
for i in range(0,n,1):
# Termino de Lagrange
termino = 1
for j in range(0,n,1):
if (j!=i):
termino = termino*(x-xi[j])/(xi[i]-xi[j])
polinomio = polinomio + termino*yi[i]
# Expande el polinomio
polinomio = polinomio.expand()
return(polinomio)
# INGRESO
M = [[ 0, 0, 0, 0 ],
[11.0000, 13.0813, 14.4768, 15.5563],
[18.4997, 22.0000, 24.3470, 26.1626],
[25.0746, 29.8189, 33.0000, 35.4608]]
li = [0, 10, 20, 30]
kj = [10, 20, 30, 40]
l_busca = 25 # trabajadores
k_busca = 25 # inversion en miles de $
# PROCEDIMIENTO
M = np.array(M)
tamano = np.shape(M)
n = tamano[0]
m = tamano[1]
x,K,L = sym.symbols('x,K,L')
# Literal a.1 Interpola polinomio pk
# por fila de trabajadores L
# evalua en k_busca, inversiones en miles
poli_fila = []
pk_columna =[]
for fila in range(0,n,1):
pk = interpola_lagrange(kj,M[fila,:])
pk = pk.subs(x,K)
poli_fila.append(pk)
pk_busca = poli_fila[fila].subs(K,k_busca)
pk_columna.append(pk_busca)
# Interpola un polinomio en columna de inversiones pk_columna
# evalua en l_busca
pkl_busca = interpola_lagrange(li,pk_columna)
pkl_busca = pkl_busca.subs(x,L)
Ykl_busca = pkl_busca.subs(L,l_busca)
# SALIDA
np.set_printoptions(precision=4)
print(' **** literal a:')
print('___ Polinomio por fila de trabajadores L')
for fila in range(0,n,1):
print(fila,', L['+str(fila)+']=',li[fila], ', pk(K) :')
print(poli_fila[fila])
print(' pk['+str(k_busca)+']:',pk_columna[fila])
print('___')
print('\n Datos para el polinomio de L')
print(' Li: ',li)
print('k_busca: ',pk_columna)
print('Polinomio p(L):')
print(pkl_busca)
print('Y[l_busca,k_busca]: ',Ykl_busca)
# Grafica de P(k) por cada L
muestras = 20
xk = np.linspace(min(kj),max(kj),muestras)
plt.subplot(121)
for fila in range(0,n,1):
pk = poli_fila[fila]
if pk.has(K):
pk_lambda = sym.lambdify(K,pk)
pkx = pk_lambda(xk)
else:
nk = len(xk)
pkx = np.ones(nk)*float(pk)
plt.plot(xk,pkx, label='pk(K);li='+str(li[fila]))
plt.plot(k_busca,pk_columna[fila],'o')
plt.ylabel('p(K)')
plt.xlabel('K inversiones en miles')
plt.axvline(k_busca, linestyle ='dashed')
plt.title('Polinomios pk(K)')
plt.legend()
# Grafica de p(L) en k_busca
xl = np.linspace(min(li),max(li),muestras)
pl_lambda = sym.lambdify(L,pkl_busca)
plx = pl_lambda(xl)
plt.subplot(122)
plt.plot(xl,plx, label='p(L)')
plt.plot(li,pk_columna,'o', label='[li,pk(K)]')
plt.axvline(l_busca, linestyle ='dashed')
plt.plot(l_busca,Ykl_busca,'o')
plt.ylabel('p(L)')
plt.xlabel('L trabajadores')
plt.title('Polinomio pl(L)')
plt.legend()
# plt.show()
# Grafica 3D
from mpl_toolkits.mplot3d import axes3d
X, Y = np.meshgrid(kj,li)
figura = plt.figure()
ax = figura.add_subplot(111, projection = '3d')
ax.plot_wireframe(X,Y,M)
ax.plot(k_busca,l_busca,Ykl_busca,'o',label='(25,25,Y)')
ax.plot(k_busca*np.ones(len(li)),li,pk_columna,'o')
ax.set_xlabel('K inversion')
ax.set_ylabel('L trabajadores')
ax.set_zlabel('Y producción')
ax.set_title('Cobb-Douglas')
plt.show()
[ a1 interpola filas ] [a2 interpola punto Y] [ b1 interpola columnas ] [ b2 raíz Newton-Raphson] [ Algoritmo ]
Instrucciones en Python. literal b
#1Eva_IIIT2007_T2 Función Cobb-Douglas
# Interpolacion de Lagrange # Newton-Raphson
import numpy as np
import matplotlib.pyplot as plt
def newton_raphson(fx,dfx,xi, tolera, iteramax=100, vertabla=False, precision=4):
'''
funciónx y fxderiva en forma numérica lambda
xi es el punto inicial de búsqueda
'''
itera=0
tramo = abs(2*tolera)
if vertabla==True:
print('i', ['xi','fi','dfi', 'xnuevo', 'tramo'])
np.set_printoptions(precision)
while (tramo>=tolera and itera<iteramax):
fi = fx(xi)
dfi = dfx(xi)
xnuevo = xi - fi/dfi
tramo = abs(xnuevo-xi)
if vertabla==True:
print(itera,np.array([xi,fi,dfi,xnuevo,tramo]))
xi = xnuevo
itera = itera + 1
if itera>=iteramax:
xi = np.nan
print('itera: ',itera, 'No converge,se alcanzó el máximo de iteraciones')
return(xi)
# INGRESO
y_busca = 30
fx = lambda K: 0.0001218125*K**3 - 0.0140857812500013*K**2 + 0.748676562500027*K + 15.5417812499999 -y_busca
dfx = lambda K: 0.00036543*K**2 - 0.02817*K + 0.748676562500027
x0 = 30
tolera = 0.00001
muestras = 20
# PROCEDIMIENTO
respuesta = newton_raphson(fx,dfx,x0, tolera, vertabla=True)
# SALIDA
print('raíz en: ', respuesta)
# Grafica
xl = np.linspace(0,40,muestras)
plx = fx(xl)
plt.plot(xl,plx, label='Y(k)')
plt.axhline(0,linestyle='dotted')
plt.ylabel('f(K)')
plt.xlabel('K inversiones en miles')
plt.title('f(K) = Y(K)-'+str(y_busca))
plt.show()
[ a1 interpola filas ] [a2 interpola punto Y] [ b1 interpola columnas ] [ b2 raíz Newton-Raphson] [ Algoritmo ]


![Cobb Douglas Y[L,K]](http://blog.espol.edu.ec/analisisnumerico/files/2017/11/CobbDouglas01.png)