[ Bisección ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..
1. Ejercicio
Referencia: Burden 2.1 ejemplo 1 p38
La ecuación mostrada tiene una raíz en [1,2], ya que f(1)=-5 y f(2)=14 y existe cambio de signo. Muestre los resultados parciales del algoritmo de la bisección con una tolerancia de 0.0001
f(x) = x^3 + 4x^2 -10 =0[ Bisección ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [función]
..
2. Desarrollo Analítico
El desarrollo del ejercicio tradicionalmente realizado con lápiz, papel y calculadora, muestra el orden y detalle de las operaciones que se pueden traducir a un algoritmo en Python. El objetivo además de desarrollar la comprensión del método, permite en una evaluación observar si el estudiante conoce el método y usa apropiadamente los valores en cada iteración.
iteración 1
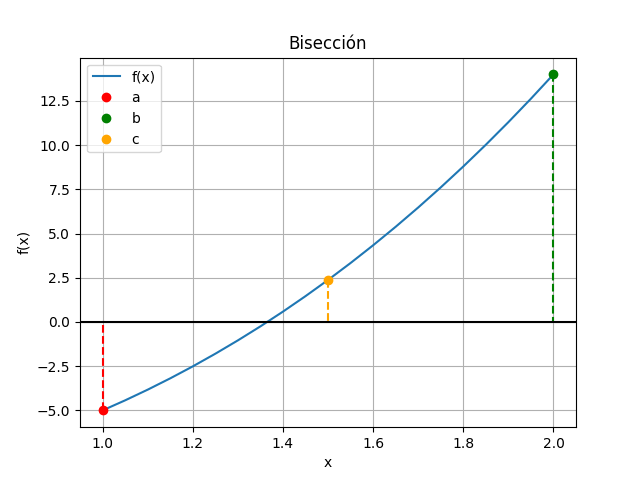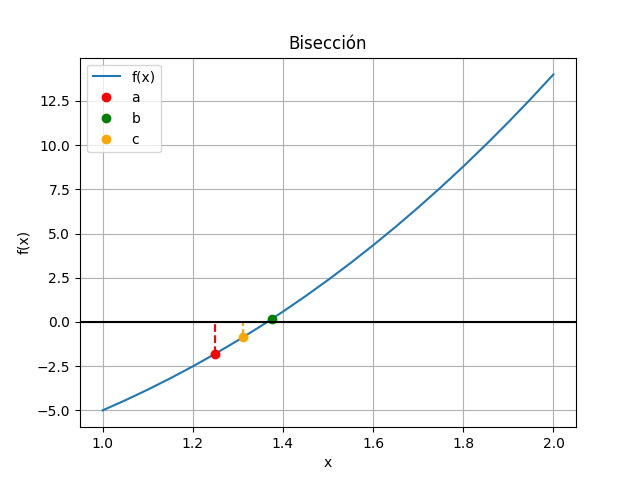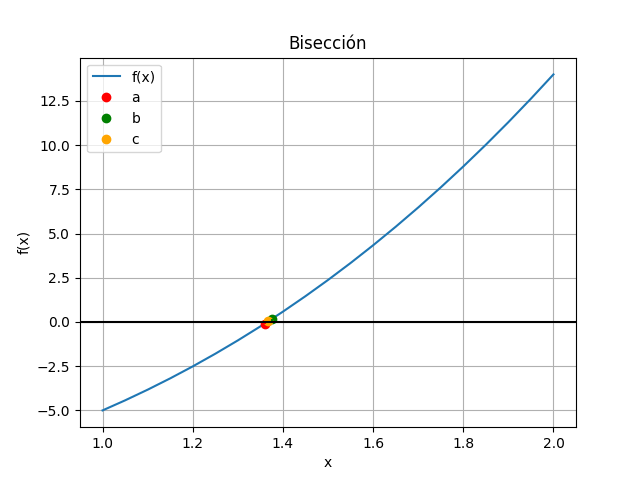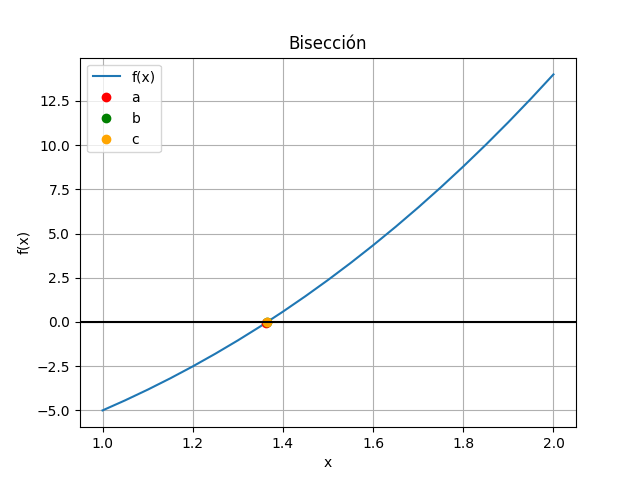
a = 1, b=2 c = \frac{a+b}{2} = \frac{1+2}{2} = 1.5 f(1) = (1)^3 + 4(1)^2 -10 = -5 f(1.5) = (1.5)^3 + 4(1.5)^2 -10= 2.37 f(2) = (2)^3 + 4(2)^2 -10 =14cambio de signo a la izquierda
a = 1, b= c = 1.5 tramo = |1.5-1| =0.5iteración 2
a = 1, b=1.5 c = \frac{1+1.5}{2} = 1.25 f(1) = -5 f(1.25) = (1.25)^3 + 4(1.25)^2 -10 = -1.794 f(1.5) = 2.37cambio de signo a la derecha
a = c = 1.25, b=1.5 tramo = |1.5-1.25| = 0.25iteración 3
continuar como tarea.
La tabla resume los valores de las iteraciones
| i | a | c | b | f(a) | f(c) | f(b) | tramo |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1.5 | 2 | -5 | 2.37 | 14 | 0.5 |
| 2 | 1 | 1.25 | 1.5 | -5 | -1.79 | 2.37 | 0.25 |
| 3 | 1.25 | … | 1.5 |
La misma tabla se puede realizar con un algoritmo para tener los resultados más rápido y observar el comportamiento del método.
Observe los resultados de f(c), principalmente en la iteración i=9 con tramo=0.00097 que representa el error de estimación del valor vs tolerancia.
i ['a', 'c', 'b'] ['f(a)', 'f(c)', 'f(b)'] tramo 0 [1, 1.5, 2] [-5. 2.375 14. ] 0.5 1 [1, 1.25, 1.5] [-5. -1.7969 2.375 ] 0.25 2 [1.25, 1.375, 1.5] [-1.7969 0.1621 2.375 ] 0.125 3 [1.25, 1.3125, 1.375] [-1.7969 -0.8484 0.1621] 0.0625 4 [1.3125, 1.34375, 1.375] [-0.8484 -0.351 0.1621] 0.03125 5 [1.34375, 1.359375, 1.375] [-0.351 -0.0964 0.1621] 0.015625 6 [1.359375, 1.3671875, 1.375] [-0.0964 0.0324 0.1621] 0.0078125 7 [1.359375, 1.36328125, 1.3671875] [-0.0964 -0.0321 0.0324] 0.00390625 8 [1.36328125, 1.365234375, 1.3671875] [-3.2150e-02 7.2025e-05 3.2356e-02] 0.001953125 9 [1.36328125, 1.3642578125, 1.365234375] [-3.2150e-02 -1.6047e-02 7.2025e-05] 0.0009765625 raíz en: 1.3642578125 >>>
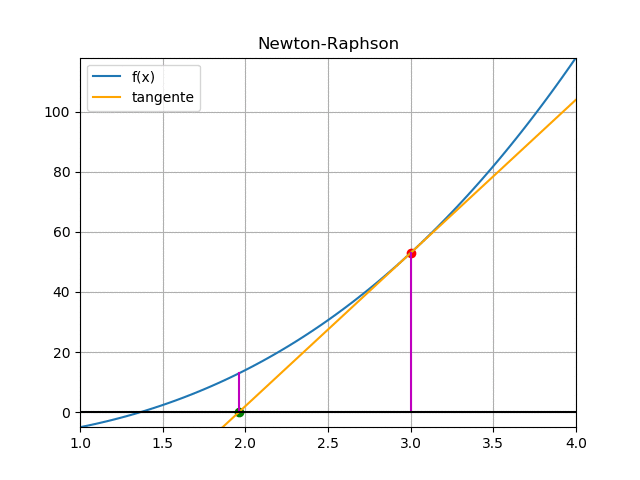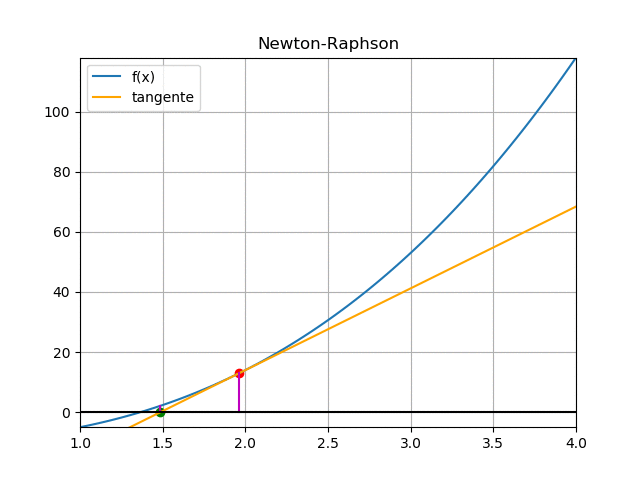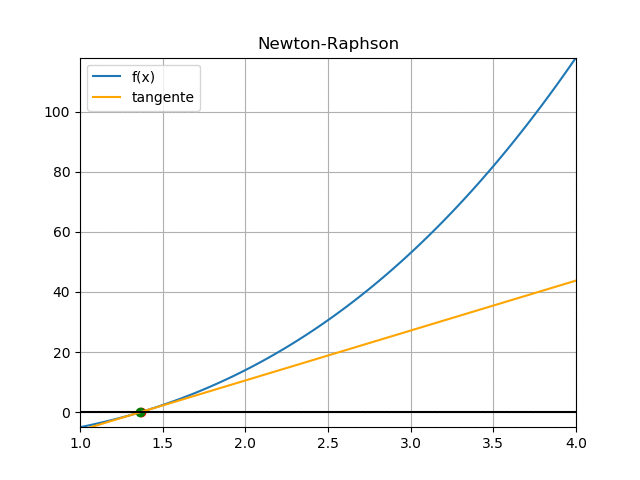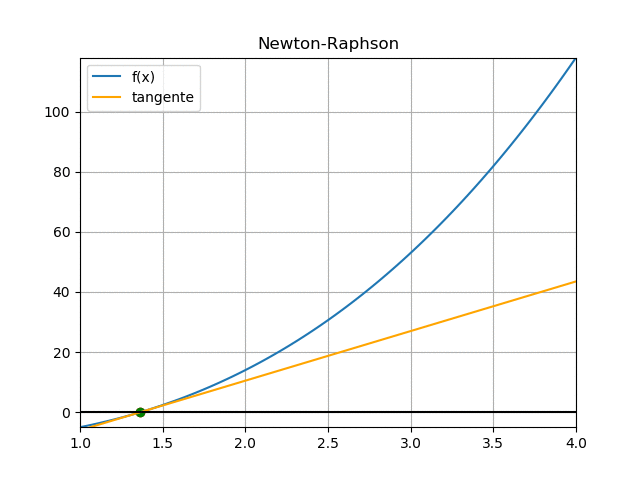
Se realiza la gráfica los puntos [c,f(c)] de la tabla para observar el resultado, resaltando que los puntos al final se aglomeran alrededor de la solución o raíz de la ecuación.
[ Bisección ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [función]
..
3. Algoritmo en Python
El video presenta el desarrollo básico conceptual del algoritmo en Python para una comprensión del proceso paso a paso.
Instrucciones en Python del Algoritmo básico del video
# Algoritmo de Bisección # [a,b] se escogen de la gráfica de la función # error = tolera import numpy as np import matplotlib.pyplot as plt # INGRESO fx = lambda x: x**3 + 4*x**2 - 10 a = 1 b = 2 tolera = 0.001 # PROCEDIMIENTO tramo = b-a while not(tramo<tolera): c = (a+b)/2 fa = fx(a) fb = fx(b) fc = fx(c) cambia = np.sign(fa)*np.sign(fc) if cambia < 0: a = a b = c if cambia > 0: a = c b = b tramo = b-a # SALIDA print(' raiz en: ', c) print('error en tramo: ', tramo)
[ Bisección ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [función]
4. Función en Python
El algoritmo presentado en el video se puede mejorar, por ejemplo simplificando las dos condicionales en uno.
Considere que en cada iteración se evalúa la función en tres puntos y se puede optimizar sustituyendo los valores de los extremos y solo evaluando el centro.
Finalmente se puede convertir el procedimiento en una función de Python.
Instrucciones en Python
# Algoritmo de Bisección # [a,b] se escogen de la gráfica de la función # error = tolera import numpy as np def biseccion(fx,a,b,tolera,iteramax = 20, vertabla=False, precision=4): ''' Algoritmo de Bisección Los valores de [a,b] son seleccionados desde la gráfica de la función error = tolera ''' fa = fx(a) fb = fx(b) tramo = np.abs(b-a) itera = 0 cambia = np.sign(fa)*np.sign(fb) if cambia<0: # existe cambio de signo f(a) vs f(b) if vertabla==True: print('método de Bisección') print('i', ['a','c','b'],[ 'f(a)', 'f(c)','f(b)']) print(' ','tramo') np.set_printoptions(precision) while (tramo>=tolera and itera<=iteramax): c = (a+b)/2 fc = fx(c) cambia = np.sign(fa)*np.sign(fc) if vertabla==True: print(itera,[a,c,b],np.array([fa,fc,fb])) if (cambia<0): b = c fb = fc else: a = c fa = fc tramo = np.abs(b-a) if vertabla==True: print(' ',tramo) itera = itera + 1 respuesta = c # Valida respuesta if (itera>=iteramax): respuesta = np.nan else: print(' No existe cambio de signo entre f(a) y f(b)') print(' f(a) =',fa,', f(b) =',fb) respuesta=np.nan return(respuesta) # INGRESO fx = lambda x: x**3 + 4*x**2 - 10 a = 1 b = 2 tolera = 0.001 # PROCEDIMIENTO respuesta = biseccion(fx,a,b,tolera,vertabla=True) # SALIDA print('raíz en: ', respuesta)
La gráfica se puede obtener añadiendo las siguientes instrucciones:
# GRAFICA import matplotlib.pyplot as plt muestras = 21 xi = np.linspace(a,b,muestras) fi = fx(xi) plt.plot(xi,fi, label='f(x)') plt.axhline(0) plt.xlabel('x') plt.ylabel('f(x)') plt.grid() plt.legend() plt.show()
Scipy.optimize.bisect
El método de la bisección se encuentra también implementado en las librería Scipy, que también puede ser usado de la forma:
>>> import scipy.optimize as opt
>>> fx = lambda x: x**3 + 4*x**2 - 10
>>> opt.bisect(fx,1,2,xtol=0.001)
1.3642578125
que es el valor de la variable ‘a’ de la tabla para la última iteración del ejercicio. Lo que muestra que el algoritmo realizado tiene un valor más aproximado.
Sin embargo por didáctica y mejor comprensión de los métodos y su implementación en algoritmos que es parte del objetivo de aprendizaje, se continuará desarrollando la forma básica en Python.
Referencia: https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.bisect.html
[ Bisección ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [función]