1.2 Error-por tipos en computadoras

Referencia: Chapra 3.3 p56, Burden definición 1.15 p14

Error: [ Absoluto ] [ Relativo ] [ Redondeo ] [ Redondeo Absoluto ]
[ Redondeo Relativo ] [ truncamiento ]
..

1. Error absoluto

Es la magnitud (sin signo) entre el valor «conocido» real X y el valor «estimado» X_k.

$E = |X-X_k|$

El valor dependerá de la magnitud de X, por ejemplo:

– Al contar monedas de 1 centavo, una persona cuenta X_k = 98 y una máquina contadora de monedas determina que el valor X = 100, el error absoluto es de 2 centavos ó 0.02 dólares.

¿Que pasaría si el conteo fuese con monedas de 1 dólar y se mantienen las mismas cantidades de monedas?

Error: [ Absoluto ] [ Relativo ] [ Redondeo ] [ Redondeo Absoluto ]
[ Redondeo Relativo ] [ truncamiento ]
..

2. Error relativo

Continuando el tema del ejemplo anterior, se puede mejorar dimensionando proporcionalmente los errores, es decir ponderarlos respecto a la magnitud usada.

$e = \frac{|X-X_k|}{X}$

Ponderar el error, calculando el error relativo para ambos ejemplos anteriores, se hacen comparables cuando las monedas son de un centavo o un dolar:

e = \frac{|100-98|}{100} = 0.02

Error: [ Absoluto ] [ Relativo ] [ Redondeo ] [ Redondeo Absoluto ]
[ Redondeo Relativo ] [ truncamiento ]
..

3. Error de redondeo

Aparece cuando se usa una calculadora o computadora para los cálculos con números reales. La calculadora usa una cantidad finita de dígitos.
Por ejemplo:

el número π tiene un número infinito de dígitos,
si el número resultante de $\sqrt{3}$ se eleva al cuadrado, se debería obtener 3

Sin embargo podemos comprobar que lo enunciado no se cumple al usar el computador, así obtenemos el error de redondeo.

Usando Python se obtiene:

>>> import numpy as np
>>> numeropi=np.pi
>>> numeropi
3.141592653589793

>>> b=np.sqrt(3)
>>> b
1.7320508075688772
>>> b**2
2.9999999999999996
>>>

Error: [ Absoluto ] [ Relativo ] [ Redondeo ] [ Redondeo Absoluto ]
[ Redondeo Relativo ] [ truncamiento ]..

4. Error de redondeo absoluto

si $X_k$ es una aproximación de X, el error absoluto es

E = |X-X_k|

Este error se enfoca solo en la magnitud de las diferencias, no importa el signo.

Error: [ Absoluto ] [ Relativo ] [ Redondeo ] [ Redondeo Absoluto ]
[ Redondeo Relativo ] [ truncamiento ]
..

5. Error de redondeo relativo

El error relativo es más significativo al usar la proporción del error en lugar del tamaño del valor.

e = \frac{|X-X_k|}{X}

Error: [ Absoluto ] [ Relativo ] [ Redondeo ] [ Redondeo Absoluto ]
[ Redondeo Relativo ] [ truncamiento ]
..

6. Error de truncamiento

Resultan al usar una aproximación en lugar de un procedimiento matemático exacto. Es la diferencia entre una respuesta esperada y el valor calculado con una fórmula iterativa.

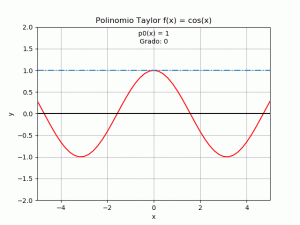
Ejemplo, al usar un polinomio de Taylor en lugar de la función original f(x).

Error: [ Absoluto ] [ Relativo ] [ Redondeo ] [ Redondeo Absoluto ]
[ Redondeo Relativo ] [ truncamiento ]