1.3 Aproximación numérica – Máximo en intervalo

Ejemplo: [ 1. Máximo en intervalo ] [ 2. Máximo en intervalo ]
..

Ejemplo 1 . Máximo en intervalo

Referencia: Burden 7Ed capítulo 1.1-ejemplo 1 p6; Burden 10Ed p5

Determine el valor máximo de |f(x)| en los intervalos: [1, 2] y [0.5, 1]. Siendo la función:

f(x) = 5 \cos(2x) - 2x \sin(2x)

Se puede usar dos opciones para el desarrollo: la analítica y la numérica.

1.1 Solución analítica

Se determina la derivada de f(x) y se determina el valor de x cuando f'(x) toma el valor de cero.

f(x) = 5 \cos(2x) - 2x \sin(2x)

f'(x) = 5 (- 2 \sin(2x)) - [2x (2 \cos(2x)) + 2 \sin(2x) ]

f'(x) = - 12 \sin(2x) - 4x \cos(2x)

f'(x) en el rango [1,2] toma el valor de cero en:

0 = - 12 \sin(2x) - 4x \cos(2x)

Situación que requiere un poco de trabajo adicional para encontrar el punto buscado…

1.2 Solución numérica

Otra forma es determinar el valor usando un método numérico, cuya precisión dependerá de la cantidad de muestras discreta, o tamaño de paso, que se utilicen para la evaluación.

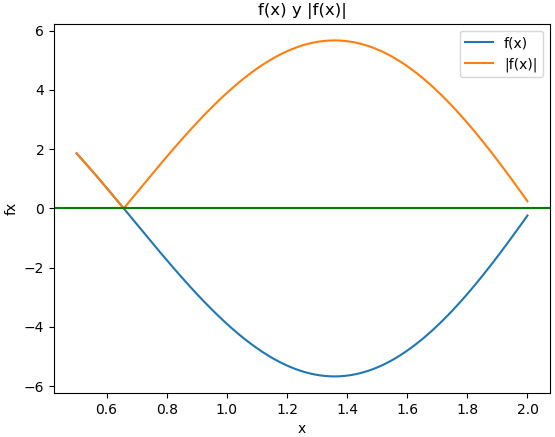
Una gráfica permite estimar las intersecciones con los ejes y extremos de las funciones.

el máximo se encuentra en: 1.358
con el valor f(x) de: 5.67530054527

El valor máximo de |fx| en magnitud se cumple cuando la derivada es cero en un punto del intervalo.

Algoritmo en Python

Para observar la función, se realiza la gráfica en el rango [0.5, 2].
El algoritmo base corresponde al usado para una gráfica 2D, si no dispones de información previa, consulte el enlace: Gráficas 2D de línea
La función fx se escribe en formato lambda por simplicidad. Si no tiene información previa sobre funciones numéricas en formato lambda revise el enlace: Funciones def-return vs lambda.
La precisión a usar es de mil tramos, o mil uno muestras en el intervalo [a,b], que es (2-0.5)/1000 = 0.0015‬
Se usa el algoritmo de búsqueda de posición del valor mayor en la función valor absoluto «fxabs».

Las instrucciones usadas en Python son:

# Burden capítulo 1.1-ejemplo 1 p6, pdf16
# Determine el maximo entre [a,b] para fx
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
fx = lambda x: 5*np.cos(2*x)-2*x*np.sin(2*x)
a = 0.5
b = 2
muestras = 1001

# PROCEDIMIENTO
xi = np.linspace(a,b,muestras)
fi = fx(xi)

fiabs = np.abs(fi)
donde = np.argmax(fiabs)

# SALIDA
print('el máximo se encuentra en: ', xi[donde])
print('con el valor f(x): ', fiabs[donde])

# GRAFICA
plt.plot(xi,fi, label='f(x)')
plt.plot(xi,fiabs, label='|f(x)|')
plt.axhline(y=0, color='g')
plt.xlabel('x')
plt.ylabel('fx')
plt.legend()
plt.title('f(x) y |f(x)|')
plt.show()

1.3 Usando Scipy.Optimize

La librería Scipy dispone de varios algoritmos de optimización que se desarrollarán durante el curso.

La comprensión de cada uno de ellos permite una aplicación efectiva de los algoritmos para obtener el resultado buscado.

Por ejemplo, usando la derivada de la función y un punto de partida x₀ donde se supone, intuye o cercano donde se pretende obtener, se busca cuándo su valor es mínimo con la instrucción fsolve() se obtiene:

[ 1.35822987]
>>>

las instrucciones del algoritmo son:

# Burden capítulo 1.1-ejemplo 1 p6, pdf16
# Determine el maximo entre [a,b] para fx
# Encontrar el máximo cuando f'(x) pasa por cero

import numpy as np
import scipy.optimize as opt

# INGRESO
fx = lambda x: 5*np.cos(2*x)-2*x*np.sin(2*x)
dfx = lambda x: -12*np.sin(2*x)-4*x*np.cos(2*x)
a = 0.5
b = 2
muestras = 1001
x0 = 1 # punto inicial de búsqueda

# PROCEDIMIENTO
dondemax  = opt.fsolve(dfx,x0)

# SALIDA
print(dondemax)

compare con los resultados anteriores.

Ejemplo: [ 1. Máximo en intervalo ] [ 2. Máximo en intervalo ]
..

Ejemplo 2. Máximo en un intervalo

Referencia: Burden 7Ed Capítulo 1.1 Ejercicio 3a p15, Burden 10Ed p6

Demuestre que f'(x) se anula al menos una vez en el intervalo [0,1].

f(x) = 1 - e^{x} + (e-1)sen \Big( \frac{\pi}{2}x \Big)

2.1 Desarrollo analítico

Se usa el «teorema de Rolle«, si los extremos del intervalo son iguales, existe un punto intermedio c en el que la derivada es cero, en donde la función tiene un máximo.

f(0) = 1 - e^{0} + (e-1)sen(\frac{\pi}{2}0) =

= 1 - 1 + (e-1)(0) = 0

f(1) = 1 - e^{1} + (e-1)sen(\frac{\pi}{2}1) =

= 1 - e + (e-1)(1) = 0

f(0) = f(1)

por el teorema, debe existir un máximo, o existe un c tal que f'(c) = 0.

2.2 Desarrollo numérico y gráfico

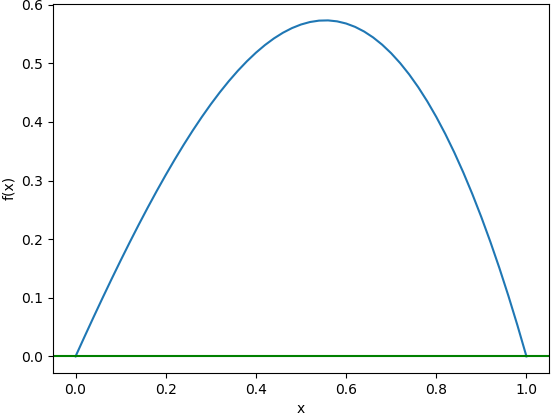
Para encontrar el máximo, se evalúa en los extremos, se aplica Rolle y como comprobación se muestra la gráfica.

Puntos en extremos de intervalo
(xi,fi)
0 0.0
1 0.0

Algoritmo en Python

Semejante al ejercicio anterior, el punto de partida es el algoritmo para gráficas 2D.

Se plantea la función en formato lambda, usando el intervalo con 50 tramos o

# Burden Capítulo 1.1 Ejercicio 3a p15, pdf 25
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
fx = lambda x: 1-np.exp(x)+(np.exp(1)-1)*np.sin((np.pi/2)*x)
a = 0
b = 1
muestras = 51

# PROCEDIMIENTO
fa = fx(a)
fb = fx(b)

xi = np.linspace(a,b,muestras)
fi = fx(xi)

# SALIDA
print('Puntos en extremos de intervalo')
print('[xi,fi]')
print(a,fa)
print(b,fb)

# GRAFICA
plt.plot(xi,fi)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.axhline(0,color='g')
plt.show()

añada las instrucciones para encontrar el punto donde f'(x) pasa por cero, que es donde existe el máximo. use como referencia el ejemplo 1.

Ejemplo: [ 1. Máximo en intervalo ] [ 2. Máximo en intervalo ]