[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..
1. Ejercicio
Referencia: Burden 2.1 ejemplo 1 p38
La ecuación mostrada tiene una raíz en el intervalo [1,2], ya que f(1) = -5 y f(2) = 14. Muestre los resultados parciales del algoritmo de la secante con una tolerancia de 0.0001
f(x) = x^3 + 4x^2 -10 =0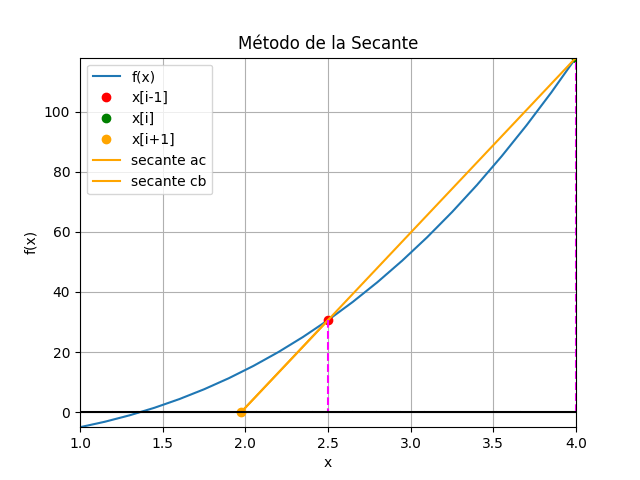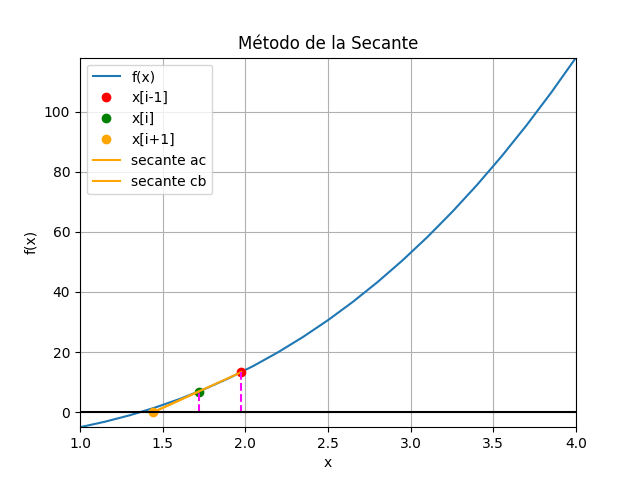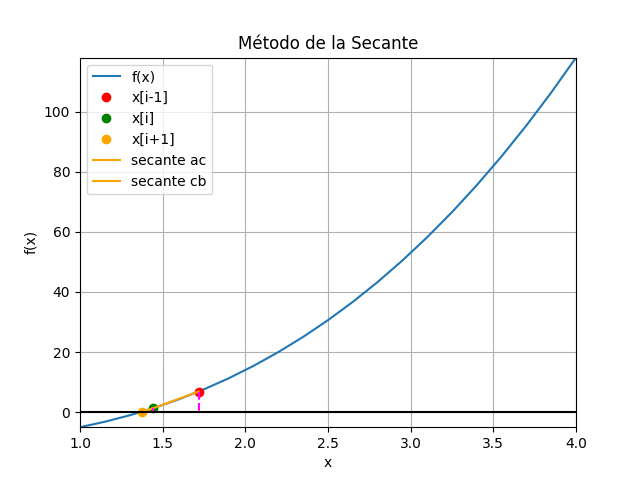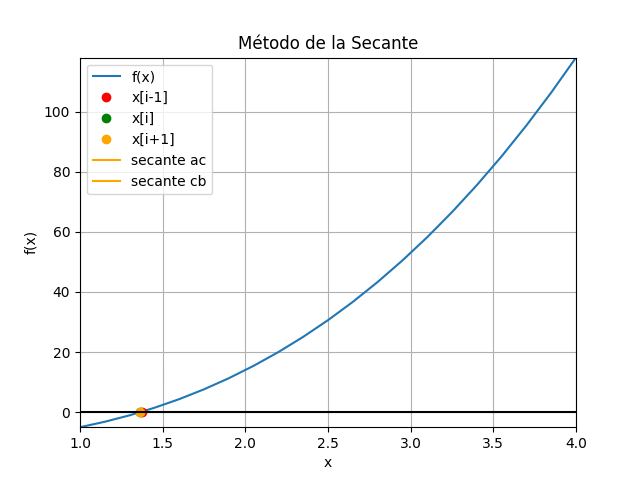
La gráfica se realiza iniciando con los valores 2.5 y 4 para observar mejor el efecto gráfico en las iteraciones.
[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [función]
..
2. Desarrollo Analítico
f(x) = x^3 + 4x^2 -10 =0 x_{i+1}= x_i - f(x_i)\frac{(x_{i-1} - x_i)}{f(x_{i-1}) - f(x_i)}Se probará con valores iniciales dentro del tramo [1,2], tolera = 0.001
itera = 0
X-1 = 1, X0 =2,
f(1) = (1)^3 + 4(1)^2 -10 = -5 f(2) = (2)^3 + 4(2)^2 -10 =14 x_{1}= 2 - 14\frac{(1 - 2)}{(-5 - 14)} = 1.2632 errado = |1.2632 - 2| = 0.7368itera = 1
X0 = 2, X1 = 1.2632
f(2) =14 f(1.2632) = ( 1.2632)^3 + 4( 1.2632)^2 -10 =-1.6023 x_{2}= 1.2632 - (-1.6023)\frac{(2 - 1.2632)}{(14 -(-1.6023))} =1.3388 errado = |1.3388 - 1.2632 | = 0.0756itera = 2
X1 =1.2632, X2 =1.3388
f(1.2632) = -1.6023 f(1.3388) = (1.3388)^3 + 4(1.3388)^2 -10 =-0.4304 x_{3}= 1.3388 - (-0.4304)\frac{(1.2632 - 1.3388)}{(-1.6023 -(-0.4304))} = 1.3666 errado = | 1.3388- 1.3666| =0.0277desarrollando una tabla con el algoritmo se tiene:
método de la Secante i [ x[i-1], xi, x[i+1], f[i-1], fi ] tramo 0 [ 1. 2. 1.2632 -5. 14. ] 0.736842105263158 1 [ 2. 1.2632 1.3388 14. -1.6023] 0.0756699440909967 2 [ 1.2632 1.3388 1.3666 -1.6023 -0.4304] 0.027788555891506528 3 [ 1.3388 1.3666 1.3652 -0.4304 0.0229] 0.001404492087488718 4 [ 1.3666e+00 1.3652e+00 1.3652e+00 2.2909e-02 -2.9907e-04] 1.809847900258177e-05 raíz: 1.3652300011108591 tramo: 1.809847900258177e-05 itera: 5
[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..
3. Algoritmo en Python
Para identificar los puntos consecutivos con variables simples, se usa la siguiente conversión:
| xi-1 | xi | xi+1 |
| xa | xb | xc |
Instrucciones en Python
# Método de secante import numpy as np # INGRESO fx = lambda x: x**3 + 4*x**2 - 10 a = 1 # intervalo de búsqueda b = 2 tolera = 0.001 iteramax = 20 # PROCEDIMIENTO xa = a xb = b itera = 0 tramo = 2*tolera while tramo>tolera and itera<iteramax: fa = fx(xa) fb = fx(xb) xc = xb - fb*(xa - xb)/(fa - fb) tramo = abs(xc - xb) xa = xb xb = xc itera = itera + 1 if itera>=iteramax: # revisa convergencia xc = np.nan # SALIDA print('raiz:',xc) print('tramo:',tramo) print('itera:',itera)
[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..
4. Función en Python
Una función resumida, se recomienda realizar la validación de cambio de signo entre [a,b]
# Método de secante import numpy as np def secante_raiz(fx,a,b,tolera, iteramax=20, vertabla=True, precision=6): '''fx en forma numérica lambda Los valores de [a,b] son seleccionados desde la gráfica de la función ''' xa = a xb = b itera = 0 tramo = np.abs(xb-xa) if vertabla==True: print('método de la Secante') print('i','[ x[i-1], xi, x[i+1], f[i-1], fi ]','tramo') np.set_printoptions(precision) while not(tramo<tolera or itera>iteramax): fa = fx(xa) fb = fx(xb) xc = xb - fb*(xa - xb)/(fa - fb) tramo = abs(xc - xb) if vertabla==True: print(itera,np.array([xa,xb,xc,fa,fb]),tramo) xa = xb xb = xc itera = itera + 1 if itera>=iteramax: xc = np.nan print('itera: ',itera, 'No converge,se alcanzó el máximo de iteraciones') respuesta = xc return(respuesta) # INGRESO fx = lambda x: x**3 + 4*x**2 - 10 a = 1 b = 2 tolera = 0.001 # PROCEDIMIENTO respuesta = secante_raiz(fx,a,b,tolera, vertabla=True,precision=4) # SALIDA print('raíz: ', respuesta)
5. Función en librería Scipy.optimize.newton – Secante
El método de la secante se encuentra implementado en Scipy en la forma de algoritmo de newton, que al no proporcionar la función para la derivada de f(x), usa el método de la secante:
>>> import scipy.optimize as opt >>> opt.newton(fx,xa, tol=tolera) 1.3652320383201266
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.newton.html
[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]