[ Falsa Posición ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..
1. Ejercicio
Referencia: Burden 2.1 ejemplo 1 p38
La ecuación mostrada tiene una raíz en [1,2], ya que f(1)=-5 y f(2)=14. Muestre los resultados parciales del algoritmo de la posición falsa con una tolerancia de 0.0001
f(x) = x^3 + 4x^2 -10 =0[ Falsa Posición ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..
2. Desarrollo Analítico
Semejante a los métodos anteriores, el método posición falsa, falsa posición, regla falsa o regula falsi, usa un intervalo [a,b] para buscar la raíz.
Se divide el intervalo en dos partes al calcular el punto c que divide al intervalo siguiendo la ecuación:
c = b - f(b) \frac{a-b}{f(a)-f(b)}iteración 1
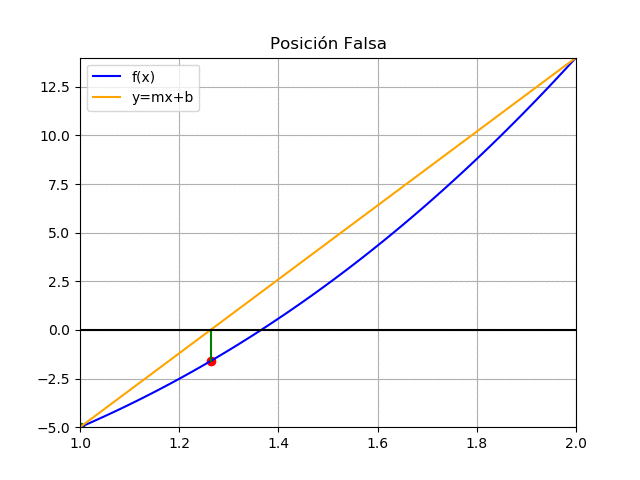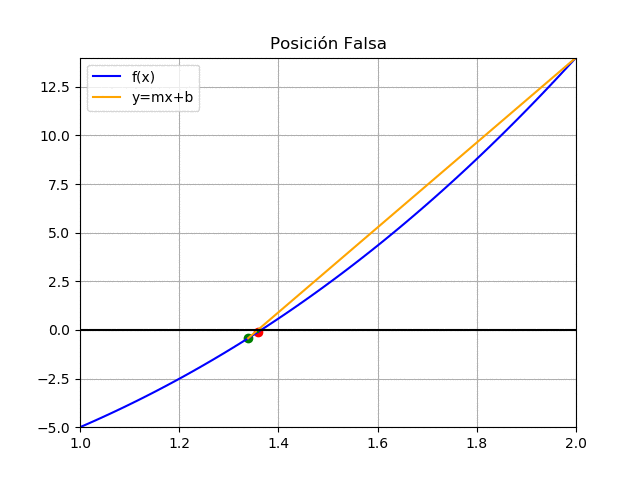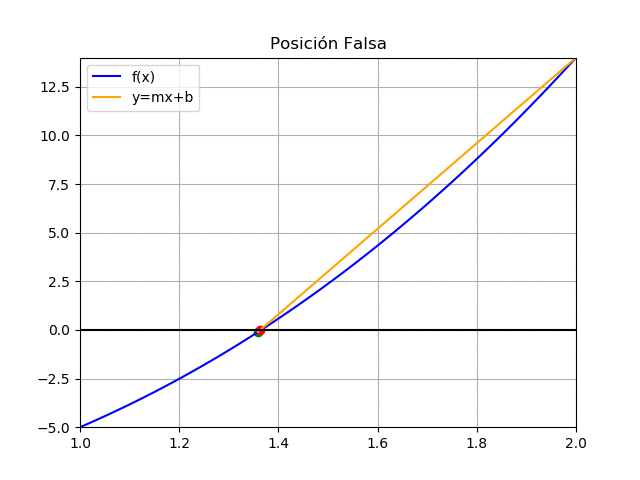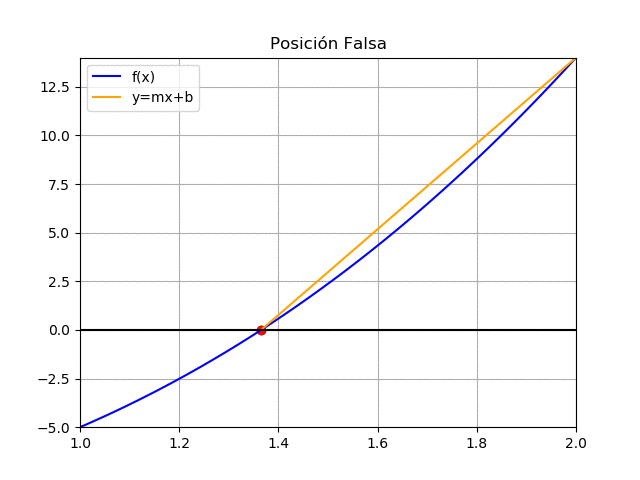
a = 1 , b = 2 f(1) = (1)^3 + 4(1)^2 -10 = -5 f(2) = (2)^3 + 4(2)^2 -10 = 14 c = 2 - 14 \frac{1-2}{-5-14} = 1.2631 f(1.2631) = (1.2631)^3 + 4(1.2631)^2 -10 = -1.6031el signo de f(c) es el mismo que f(a), se ajusta el lado izquierdo
tramo = |c-a| = | 1.2631 - 1| = 0.2631 a = c = 1.2631iteración 2
a = 1.2631 , b = 2 f(1.2631) = -1.6031 f(2) = 14 c = 2 - 14 \frac{1.2631-2}{-1.6031-14} = 1.3388 f(1.3388) = (1.3388)^3 + 4(1.3388)^2 -10 = -0.4308el signo de f(c) es el mismo que f(a), se ajusta el lado izquierdo
tramo = |c-a| = |1.3388 - 1.2631| = 0.0757 a = c = 1.3388iteración 3
a = 1.3388 , b = 2 f(1.3388) = -0.4308 f(2) = 14 c = 2 - 14 \frac{1.3388-2}{-0.4308-14} = 1.3585 f(1.3585) = (1.3585)^3 + 4(1.3585)^2 -10 = -0.1107el signo de f(c) es el mismo que f(a), se ajusta el lado izquierdo
tramo = |c-a| = |1.3585 - 1.3388| = 0.0197 a = c = 1.3585valores que se resumen en la tabla
| a | c | b | f(a) | f(c) | f(b) | tramo |
| 1 | 1.2631 | 2 | -5 | -1.6031 | 14 | 0.2631 |
| 1.2631 | 1.3388 | 2 | -1.6031 | -0.4308 | 14 | 0.0757 |
| 1.3388 | 1.3585 | 2 | -0.4308 | -0.1107 | 14 | 0.0197 |
| 1.3585 | … | 2 |
se puede continuar con las iteraciones como tarea
[ Falsa Posición ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..
3. Algoritmo en Python
Algoritmo básico del video:
# Algoritmo Posicion Falsa para raices # busca en intervalo [a,b] import numpy as np # INGRESO fx = lambda x: x**3 + 4*x**2 - 10 a = 1 b = 2 tolera = 0.001 # PROCEDIMIENTO tramo = abs(b-a) while not(tramo<=tolera): fa = fx(a) fb = fx(b) c = b - fb*(a-b)/(fa-fb) fc = fx(c) cambia = np.sign(fa)*np.sign(fc) if (cambia > 0): tramo = abs(c-a) a = c else: tramo = abs(b-c) b = c raiz = c # SALIDA print(raiz)
Algoritmo aumentado para mostrar la tabla de cálculos
# Algoritmo Posicion Falsa para raices # busca en intervalo [a,b] # tolera = error import numpy as np # INGRESO fx = lambda x: x**3 + 4*(x**2) -10 a = 1 b = 2 tolera = 0.0001 # PROCEDIMIENTO tabla = [] tramo = abs(b-a) fa = fx(a) fb = fx(b) while not(tramo<=tolera): c = b - fb*(a-b)/(fa-fb) fc = fx(c) unafila = [a,c,b,fa,fc,fb,tramo] cambio = np.sign(fa)*np.sign(fc) if cambio>0: tramo = abs(c-a) a = c fa = fc else: tramo = abs(b-c) b = c fb = fc unafila[6]=tramo tabla.append(unafila) tabla = np.array(tabla) ntabla = len(tabla) # SALIDA np.set_printoptions(precision=6) print('método de la Posición Falsa ') print('i', ['a','c','b'],[ 'f(a)', 'f(c)','f(b)']) print(' ','tramo') for i in range(0,ntabla,1): print(i, tabla[i,0:3],tabla[i,3:6]) print(' ', tabla[i,6]) print('raiz: ',c)
Observe el número de iteraciones realizadas, hasta presentar el valor de la raíz en 1.3652 con un error de 0.000079585 en la última fila de la tabla. Sin embargo, observe que la tabla solo muestra cálculos de filas completas, el último valor de c y error no se ingresó a la tabla, que se muestra como c y tramo, y es el más actualizado en los cálculos.
método de la Posición Falsa
i ['a', 'c', 'b'] ['f(a)', 'f(c)', 'f(b)']
tramo
0 [1. 1.263158 2. ] [-5. -1.602274 14. ]
0.26315789473684204
1 [1.263158 1.338828 2. ] [-1.602274 -0.430365 14. ]
0.0756699440909967
2 [1.338828 1.358546 2. ] [-0.430365 -0.110009 14. ]
0.019718502996940224
3 [1.358546 1.363547 2. ] [-0.110009 -0.027762 14. ]
0.005001098217311428
4 [1.363547 1.364807 2. ] [-2.776209e-02 -6.983415e-03 1.400000e+01]
0.0012595917846898175
5 [1.364807 1.365124 2. ] [-6.983415e-03 -1.755209e-03 1.400000e+01]
0.0003166860575976038
6 [1.365124 1.365203 2. ] [-1.755209e-03 -4.410630e-04 1.400000e+01]
7.958577822231305e-05
raíz en: 1.3652033036626001
[ Falsa Posición ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..
4. Función en Python
# Algoritmo de falsa posicion para raices # Los valores de [a,b] son seleccionados # desde la gráfica de la función # error = tolera import numpy as np def posicionfalsa(fx,a,b,tolera,iteramax = 20, vertabla=False, precision=6): '''fx en forma numérica lambda Los valores de [a,b] son seleccionados desde la gráfica de la función error = tolera ''' fa = fx(a) fb = fx(b) tramo = np.abs(b-a) itera = 0 cambia = np.sign(fa)*np.sign(fb) if cambia<0: # existe cambio de signo f(a) vs f(b) if vertabla==True: print('método de la Posición Falsa ') print('i', ['a','c','b'],[ 'f(a)', 'f(c)','f(b)']) print(' ','tramo') np.set_printoptions(precision) while (tramo >= tolera and itera<=iteramax): c = b - fb*(a-b)/(fa-fb) fc = fx(c) cambia = np.sign(fa)*np.sign(fc) if vertabla==True: print(itera,np.array([a,c,b]), np.array([fa,fc,fb])) if (cambia > 0): tramo = np.abs(c-a) a = c fa = fc else: tramo = np.abs(b-c) b = c fb = fc if vertabla==True: print(' ',tramo) itera = itera + 1 respuesta = c # Valida respuesta if (itera>=iteramax): respuesta = np.nan else: print(' No existe cambio de signo entre f(a) y f(b)') print(' f(a) =',fa,', f(b) =',fb) respuesta=np.nan return(respuesta) # PROGRAMA ---------------------- # INGRESO fx = lambda x: x**3 + 4*x**2 - 10 a = 1 b = 2 tolera = 0.0001 # PROCEDIMIENTO respuesta = posicionfalsa(fx,a,b,tolera,vertabla=True) # SALIDA print('raíz en: ', respuesta)
La gráfica se puede obtener añadiendo las siguientes instrucciones:
# GRAFICA import matplotlib.pyplot as plt muestras = 21 xi = np.linspace(a,b,muestras) fi = fx(xi) plt.plot(xi,fi, label='f(x)') plt.axhline(0) plt.xlabel('x') plt.ylabel('f(x)') plt.grid() plt.legend() plt.show()
[ Falsa Posición ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]