Ejercicio: 1Eva_IIT2009_T1 Movimiento de partícula en plano

a. Planteamiento del problema

Las ecuaciones expresan las trayectorias de dos partículas,

$x(t) = 3 \sin ^{3}(t)-1$ $y(t) = 4 \sin (t)\cos (t)$

que para que se encuentren o choquen, sus coordenadas deberían ser iguales.

$x(t) = y(t)$ $3 \sin ^{3}(t)-1 = 4 \sin (t)\cos (t)$

Se reordena la expresión, de la forma f(t) = 0 para usarla en el algoritmo de búsqueda de raíces.

$3 \sin ^{3}(t)-1 - 4 \sin (t)\cos (t) = 0$ $f(t) = 3 \sin ^{3}(t)-1 - 4 \sin (t)\cos (t)$

---

b. Intervalo de búsqueda de raíz

Como la variable independiente es tiempo, el evento a buscar se supone sucede en tiempos positivos t>=0, por lo que el valor inicial a la izquierda del intervalo será a=0

Para el caso de b, a la derecha, se usa lo indicado en el enunciado para la pregunta del literal b, donde se indica t ∈ [0, π/2], por lo que b = π/2

[0, π/2]

verificando que exista cambio de signo entre f(a) y f(b)

$f(0) = 3 \sin ^{3}(0)-1 - 4 \sin (0)\cos (0) = -1$ $f(\pi /2) = 3 \sin ^{3}(\pi /2)-1 - 4 \sin (\pi /2)\cos (\pi /2)$ $= 3 (1)^3-1 - 4 (1)(0) = 2$

con lo que se comprueba que al existir cambio de signo, debe existir una raíz en el intervalo.

---

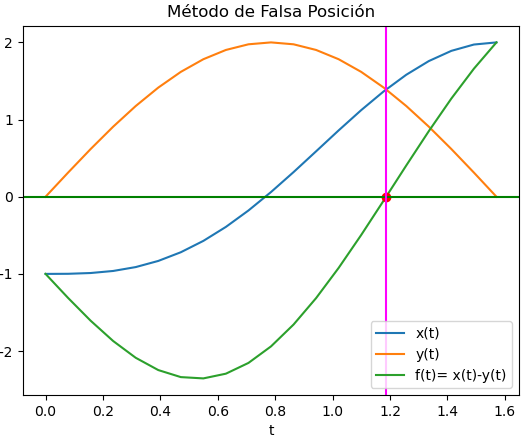
c. Método de Falsa Posición

Desarrollo analítico con lápiz y papel

Se trata de mostrar los pasos en al menos tres iteraciones del método, usando las siguientes expresiones:

$f(t) = 3 \sin ^{3}(t)-1 - 4 \sin (t)\cos (t)$ $c = b - f(b) \frac{a-b}{f(a)-f(b)}$

[0, π/2]

iteración 1

$a = 0 , b = \pi/2$

tomando los datos al validar los puntos extremos

$f(0) = -1$ $f(\pi /2) = 2$ $c = \pi/2 - 2 \frac{0-\pi/2}{-1-2} = \pi/6$ $f(\pi/6) = 3 \sin ^{3}(\pi/6)-1 - 4 \sin (\pi/6)\cos (\pi/6)$ $= -2.3570$

el signo de f(c) es el mismo que f(a), se ajusta el lado izquierdo

$tramo = |c-a| = |\pi /6 - 0| = \pi/6$ $a = c = \pi/6 , b = \pi/2$

iteración 2

$a = \pi/6 , b = \pi/2$ $f(\pi/6) = -2.3570$ $f(\pi /2) = 2$ $c = \pi/2 - 2 \frac{\pi/6-\pi/2}{-1-2} = 1.0901$ $f(1.0901) = 3 \sin ^{3}(1.0901)-1 - 4 \sin (1.0901)\cos (1.0901)$ $= -0.5486$

el signo de f(c) es el mismo que f(a), se ajusta el lado izquierdo

$tramo = |c-a| = | 1.0901-\pi/6| = 1.0722$ $a = c = 1.0901 , b = \pi/2$

iteración 3

$a = 1.0901 , b = \pi/2$ $f(1.0901) = -0.5486$ $f(\pi /2) = 2$ $c = \pi/2 - 2 \frac{-0.5486-\pi/2}{-0.5486-2} = 1.19358$ $f(1.19358) = 3 \sin ^{3}(1.19358)-1 - 4 \sin (1.19358)\cos (1.19358)$ $= 0.0409$

el signo de f(c) es el mismo que f(b), se ajusta el lado derecho

$tramo = |b-c| = | \pi/2- 1.19358| = 0.3772$ $a = 1.0901 , b = 1.19358$

---

---

Algoritmo con Python

Los parámetros aplicados en el algoritmo son los desarrollados en el planteamiento del problema e intervalo de búsqueda, con lo que se obtiene los siguientes resultados:

 raiz: 1.1864949811467547
error: 9.919955449055884e-05

las instrucciones en Python son:

# 1Eva_IIT2009_T1 Movimiento de partícula en plano
import numpy as np
import matplotlib.pyplot as plt

#INGRESO
xt = lambda t: 3*(np.sin(t)**3)-1
yt = lambda t: 4*np.sin(t)*np.cos(t)
fx = lambda t: 3*(np.sin(t)**3)-1 - 4*np.sin(t)*np.cos(t) 

a = 0
b = np.pi/2
tolera = 0.001

# intervalo para gráfica
La = a
Lb = b
muestras = 21

# PROCEDIMIENTO
# Posicion Falsa
tramo = abs(b-a)
fa = fx(a)
fb = fx(b)
while not(tramo<=tolera):
    c = b - fb*(a-b)/(fa-fb)
    fc = fx(c)
    cambio = np.sign(fa)*np.sign(fc)
    if cambio>0:
        # actualiza en izquierda
        tramo = abs(c-a)
        a = c
        b = b
        fa = fc
    else:
        # actualiza en derecha
        tramo = abs(b-c)
        a = a
        b = c
        fb = fc

# para grafica
ti = np.linspace(La,Lb,muestras)
xi = xt(ti)
yi = yt(ti)
fi = fx(ti)

# SALIDA
print(' raiz:', c)
print('error:', tramo)

# GRAFICA
plt.plot(ti,xi, label='x(t)')
plt.plot(ti,yi, label='y(t)')
plt.plot(ti,fi, label='f(t)')
plt.plot(c,fx(c),'ro')
plt.axhline(0, color='green')
plt.axvline(c, color='magenta')
plt.legend()
plt.xlabel('t')
plt.title('Método de Falsa Posición')
plt.show()