Publicado en por Edison Del Rosario

s1Eva_IT2019_T1 Oxígeno y temperatura en agua

Ejercicio: 1Eva_IT2019_T1 Oxígeno y temperatura en agua

Literal a

Se requiere un polinomio de grado 3 siendo el eje x correspondiente a temperatura. Son necesarios 4 puntos de referencia alrededor de 15 grados, dos a la izquierda y dos a la derecha.

Se observa que los datos en el eje x son equidistantes, h=8, y ordenados en forma ascendente, se cumple con los requisitos para usar diferencias finitas avanzadas. que tiene la forma de:

pn(x)=f0+Δf0h(x−x0)+ p_n (x) = f_0 + \frac{\Delta f_0}{h} (x - x_0) + +Δ2f02!h2(x−x0)(x−x1)+ + \frac{\Delta^2 f_0}{2!h^2} (x - x_0)(x - x_1) + +Δ3f03!h3(x−x0)(x−x1)(x−x2)+... + \frac{\Delta^3 f_0}{3!h^3} (x - x_0)(x - x_1)(x - x_2) + \text{...}

Tabla

xi f[xi] f[x1,x0] f[x2,x1,x0] f[x2,x1,x0] f[x3,x2,x1,x0]
8 11.5 9.9-11.5=
-1.6		 -1.5-(-1.6) =
0.1		 0.4-0.1=
0.3		 —
16 9.9 8.4-9.9=
-1.5		 -1.1-(1.5)=
0.4		 — —
24 8.4 7.3-8.4=
-1.1		 — — —
32 7.3 — — — —

Con lo que el polinomio buscado es:

p3(x)=11.5+−1.68(x−8)+ p_3 (x) = 11.5 + \frac{-1.6}{8} (x - 8) + +0.12!82(x−8)(x−16)+0.33!83(x−8)(x−16)(x−24) + \frac{0.1}{2!8^2} (x - 8)(x - 16) + \frac{0.3}{3!8^3} (x - 8)(x - 16)(x - 24)

Resolviendo y simplificando el polinomio, se puede observar que al aumentar el grado, la constante del término disminuye.

p3(x)=12.9−0.15x−0.00390625x2+0.00009765625x3 p_3(x)=12.9- 0.15 x - 0.00390625 x^2 + 0.00009765625 x^3

para el cálculo del error se puede usar un término adicional del polinomio, añadiendo un punto más a la tabla de diferencia finitas. Se evalúa éste término y se estima el error que dado que el término de grado 3 es del orden de 10-5, el error será menor. (Tarea)

p3(15)=12.9−0.15(15)−0.00390625(15)2+0.00009765625(15)3 p_3(15)=12.9- 0.15 (15) - 0.00390625 (15)^2 + 0.00009765625 (15)^3

Evaluando el polinomio en temperatura = 15:

p3(15) = 10.1006835937500

literal b

se deriva el polinomio del literal anterior y se evalúa en 16:

p3′(x)=0−0.15−0.00390625(2)x+0.00009765625(3)x2 p'_3(x)=0- 0.15 - 0.00390625 (2) x + 0.00009765625 (3)x^2 p3′(16)=0−0.15−0.00390625(2)(16)+0.00009765625(3)(16)2 p'_3(16)=0- 0.15 - 0.00390625 (2)(16) + 0.00009765625 (3)(16)^2

p’3(16) = -0.20

literal c

El valor de oxígeno usado como referencia es 9, cuyos valores de temperatura se encuentran entre 16 y 24 que se toman como rango inicial de búsqueda [a,b]. Por lo que el polinomio se iguala a 9 y se crea la forma estandarizada del problema:

p3(x)=9 p_3(x)=9 9=12.9−0.15x−0.00390625x2+0.00009765625x3 9 = 12.9- 0.15 x - 0.00390625 x^2 + 0.00009765625 x^3 12.9−0.15x−0.00390625x2+0.00009765625x3−9=0 12.9- 0.15 x - 0.00390625 x^2 + 0.00009765625 x^3 -9 = 0 f(x)=3.9−0.15x−0.00390625x2+0.00009765625x3 f(x) = 3.9- 0.15 x - 0.00390625 x^2 + 0.00009765625 x^3

Para mostrar el procedimiento se realizan solo tres iteraciones,

1ra Iteración
a=16 , b = 24, c = (16+24)/2 = 20
f(a) = 0.9, f(b) = -0.6, f(c) = 0.011
error = |24-16| = 8
como f(c) es positivo, se mueve el extremo f(x) del mismo signo, es decir a

2da Iteración
a=20 , b = 24, c = (20+24)/2 = 22
f(a) = 0.119, f(b) = -0.6, f(c) = -0.251
error = |24-20|= 4
como f(c) es negativo, se mueve el extremo f(x) del mismo signo, b

3ra Iteración
a=20 , b = 22, c = (20+22)/2 = 21
f(a) = 0.119, f(b) = -0.251, f(c) = -0.068
error = |22-20| = 2
como f(c) es negativo, se mueve el extremo f(x) del mismo signo, b
y así sucesivamente hasta que error< que 10-3

Usando el algoritmo en python se obtendrá la raiz en 20.632 con la tolerancia requerida.

Revisión de resultados

Usando como base los algoritmos desarrollados en clase:

tabla de diferencias finitas
['i', 'xi', 'fi', 'df1', 'df2', 'df3', 'df4']
[[ 0.   8.  11.5 -1.6  0.1  0.3  0. ]
 [ 1.  16.   9.9 -1.5  0.4  0.   0. ]
 [ 2.  24.   8.4 -1.1  0.   0.   0. ]
 [ 3.  32.   7.3  0.   0.   0.   0. ]]
dfinita:  [-1.6  0.1  0.3  0. ]
11.5 +
+( -1.6 / 8.0 )* ( x - 8.0 )
+( 0.1 / 128.0 )*  (x - 16.0)*(x - 8.0) 
+( 0.3 / 3072.0 )*  (x - 24.0)*(x - 16.0)*(x - 8.0) 
polinomio simplificado
9.8e-5*x**3 - 0.003923*x**2 - 0.149752*x + 12.898912
Literal a
9.8e-5*x**3 - 0.003923*x**2 - 0.149752*x + 12.898912
p(15) =  10.1007070000000

Literal b
0.000294*x**2 - 0.007846*x - 0.149752
dp(16) = -0.200024000000000
método de Bisección
i ['a', 'c', 'b'] ['f(a)', 'f(c)', 'f(b)']
   tramo
0 [16, 20.0, 24] [ 0.9     0.1187 -0.6   ]
   4.0
1 [20.0, 22.0, 24] [ 0.1187 -0.2509 -0.6   ]
   2.0
2 [20.0, 21.0, 22.0] [ 0.1187 -0.0683 -0.2509]
   1.0
3 [20.0, 20.5, 21.0] [ 0.1187  0.0246 -0.0683]
   0.5
4 [20.5, 20.75, 21.0] [ 0.0246 -0.022  -0.0683]
   0.25
5 [20.5, 20.625, 20.75] [ 0.0246  0.0013 -0.022 ]
   0.125
6 [20.625, 20.6875, 20.75] [ 0.0013 -0.0104 -0.022 ]
   0.0625
7 [20.625, 20.65625, 20.6875] [ 0.0013 -0.0045 -0.0104]
   0.03125
8 [20.625, 20.640625, 20.65625] [ 0.0013 -0.0016 -0.0045]
   0.015625
9 [20.625, 20.6328125, 20.640625] [ 0.0013 -0.0002 -0.0016]
   0.0078125
10 [20.625, 20.62890625, 20.6328125] [ 0.0013  0.0006 -0.0002]
   0.00390625
11 [20.62890625, 20.630859375, 20.6328125] [ 0.0006  0.0002 -0.0002]
   0.001953125
12 [20.630859375, 20.6318359375, 20.6328125] [ 1.9762e-04  1.5502e-05 -1.6661e-04]
   0.0009765625
raíz en:  20.6318359375

Algoritmos Python usando la función de interpolación y un procedimiento encontrado en:

Interpolación por Diferencias finitas avanzadas

Método de la Bisección – Ejemplo con Python

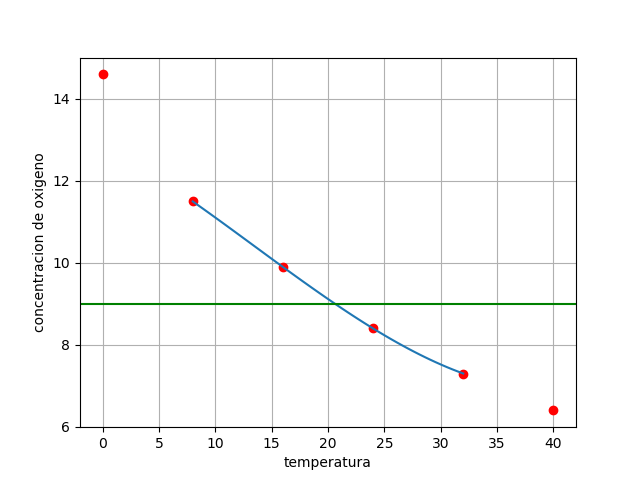
# 1Eva_IT2019_T1 Oxígeno y temperatura en mar
import numpy as np
import math
import matplotlib.pyplot as plt
import sympy as sym

def interpola_dfinitasAvz(xi,fi, vertabla=False,
                       precision=6, casicero = 1e-15):
    '''Interpolación de diferencias finitas
    resultado: polinomio en forma simbólica,
    redondear a cero si es menor que casicero 
    '''
    xi = np.array(xi,dtype=float)
    fi = np.array(fi,dtype=float)
    n = len(xi)
    # revisa tamaños de paso equidistantes
    h_iguales = pasosEquidistantes(xi, casicero)
    if vertabla==True:
        np.set_printoptions(precision)
    # POLINOMIO con diferencias Finitas avanzadas
    x = sym.Symbol('x')
    polisimple = sym.S.Zero # expresión del polinomio con Sympy
    if h_iguales==True:
        tabla,titulo = dif_finitas(xi,fi,vertabla)
        h = xi[1] - xi[0]
        dfinita = tabla[0,3:]
        if vertabla==True:
            print('dfinita: ',dfinita)
            print(fi[0],'+')
        n = len(dfinita)
        polinomio = fi[0]
        for j in range(1,n,1):
            denominador = math.factorial(j)*(h**j)
            factor = np.around(dfinita[j-1]/denominador,precision)
            termino = 1
            for k in range(0,j,1):
                termino = termino*(x-xi[k])
            if vertabla==True:
                txt1='';txt2=''
                if n<=2 or j<=1:
                    txt1 = '('; txt2 = ')'
                print('+(',np.around(dfinita[j-1],precision),
                      '/',np.around(denominador,precision),
                      ')*',txt1,termino,txt2)
            polinomio = polinomio + termino*factor
        # simplifica multiplicando entre (x-xi)
        polisimple = polinomio.expand() 
    if vertabla==True:
        print('polinomio simplificado')
        print(polisimple)
    return(polisimple)

def dif_finitas(xi,fi, vertabla=False):
    '''Genera la tabla de diferencias finitas
    resultado en: [título,tabla]
    Tarea: verificar tamaño de vectores
    '''
    xi = np.array(xi,dtype=float)
    fi = np.array(fi,dtype=float)
    # Tabla de Diferencias Finitas
    titulo = ['i','xi','fi']
    n = len(xi)
    ki = np.arange(0,n,1)
    tabla = np.concatenate(([ki],[xi],[fi]),axis=0)
    tabla = np.transpose(tabla)
    # diferencias finitas vacia
    dfinita = np.zeros(shape=(n,n),dtype=float)
    tabla = np.concatenate((tabla,dfinita), axis=1)
    # Calcula tabla, inicia en columna 3
    [n,m] = np.shape(tabla)
    diagonal = n-1
    j = 3
    while (j < m):
        # Añade título para cada columna
        titulo.append('df'+str(j-2))
        # cada fila de columna
        i = 0
        while (i < diagonal):
            tabla[i,j] = tabla[i+1,j-1]-tabla[i,j-1]
            i = i+1
        diagonal = diagonal - 1
        j = j+1
    if vertabla==True:
        print('tabla de diferencias finitas')
        print(titulo)
        print(tabla)
    return(tabla, titulo)

def pasosEquidistantes(xi, casicero = 1e-15):
    ''' Revisa tamaños de paso h en vector xi.
    True:  h son equidistantes,
    False: h tiene tamaño de paso diferentes y dónde.
    '''
    xi = np.array(xi,dtype=float)
    n = len(xi)
    # revisa tamaños de paso equidistantes
    h_iguales = True
    if n>3: 
        dx = np.zeros(n,dtype=float)
        for i in range(0,n-1,1): # calcula hi como dx
            dx[i] = xi[i+1]-xi[i]
        for i in range(0,n-2,1): # revisa diferencias
            dx[i] = dx[i+1]-dx[i]
            if dx[i]<=casicero: # redondea cero
                dx[i]=0
            if abs(dx[i])>0:
                h_iguales=False
                print('tamaños de paso diferentes en i:',i+1,',',i+2)
        dx[n-2]=0
    return(h_iguales)

# PROGRAMA ----------------

# INGRESO
tm = [0.,8,16,24,32,40]
ox = [14.6,11.5,9.9,8.4,7.3,6.4]

xi = [8,16,24,32]
fi = [11.5,9.9,8.4,7.3]

# PROCEDIMIENTO
x = sym.Symbol('x')
# literal a
polinomio = interpola_dfinitasAvz(xi,fi, vertabla=True)
p15 = polinomio.subs(x,15)
# literal b
derivap = polinomio.diff(x,1)
dp16 = derivap.subs(x,16)

px =  sym.lambdify(x,polinomio)
xk = np.linspace(np.min(xi),np.max(xi))
pk = px(xk)

# SALIDA
print('Literal a')
print(polinomio)
print('p(15) = ',p15)
print('Literal b')
print(derivap)
print('dp(16) =', dp16)

# gráfica
plt.plot(tm,ox,'ro')
plt.plot(xk,pk)
plt.axhline(9,color="green")
plt.xlabel('temperatura')
plt.ylabel('concentracion de oxigeno')
plt.grid()
plt.show()

# --------literal c ------------

def biseccion(fx,a,b,tolera,iteramax = 20, vertabla=False, precision=4):
    '''
    Algoritmo de Bisección
    Los valores de [a,b] son seleccionados
    desde la gráfica de la función
    error = tolera
    '''
    fa = fx(a)
    fb = fx(b)
    tramo = np.abs(b-a)
    itera = 0
    cambia = np.sign(fa)*np.sign(fb)
    if cambia<0: # existe cambio de signo f(a) vs f(b)
        if vertabla==True:
            print('método de Bisección')
            print('i', ['a','c','b'],[ 'f(a)', 'f(c)','f(b)'])
            print('  ','tramo')
            np.set_printoptions(precision)
            
        while (tramo>=tolera and itera<=iteramax):
            c = (a+b)/2
            fc = fx(c)
            cambia = np.sign(fa)*np.sign(fc)
            if vertabla==True:
                print(itera,[a,c,b],np.array([fa,fc,fb]))
            if (cambia<0):
                b = c
                fb = fc
            else:
                a = c
                fa = fc
            tramo = np.abs(b-a)
            if vertabla==True:
                print('  ',tramo)
            itera = itera + 1
        respuesta = c
        # Valida respuesta
        if (itera>=iteramax):
            respuesta = np.nan

    else: 
        print(' No existe cambio de signo entre f(a) y f(b)')
        print(' f(a) =',fa,',  f(b) =',fb) 
        respuesta=np.nan
    return(respuesta)
# se convierte forma de símbolos a numéricos
buscar = polinomio-9
fx = sym.lambdify(x,buscar)

# INGRESO
a = 16
b = 24
tolera = 0.001

# PROCEDIMIENTO
respuesta = biseccion(fx,a,b,tolera,vertabla=True)

# SALIDA
print('raíz en: ', respuesta)