[ Dif_Finitas ] || [ Dif_Finitas avanzadas ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] || [ Dif_Divididas_Newton ]
..
1. Interpolación por Diferencias finitas avanzadas
Referencia: Rodríguez 6.6.4 p221, Burden 9Ed p129
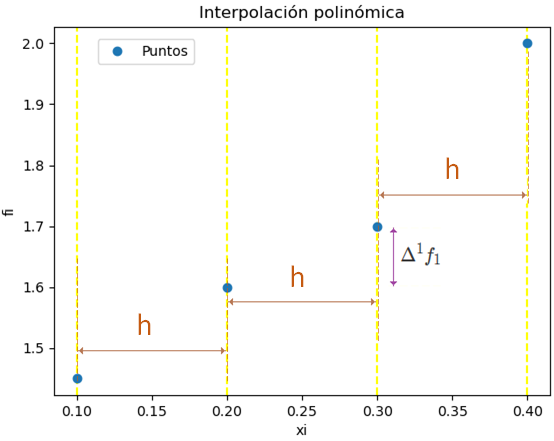
Se usa en interpolación cuando los puntos en el «eje x» se encuentran igualmente espaciados, la diferencia entre puntos consecutivos xi es una constante denominada h.
h = xi+1 – xi
Una relación entre derivadas y diferencias finitas se establece mediante:
f^{(n)}(z) = \frac{\Delta ^{n} f_{0}}{h^{n}} para algún k en el intervalo [x0,xn]
\frac{\Delta ^{n} f_{0}}{h^{n}} es una aproximación para la n-ésima derivada f(n) en el intervalo [x0,xn]
El polinomio de interpolación se puede construir por medio de diferencias finitas avanzadas con las siguiente fórmula:
p_n (x) = f_0 + \frac{\Delta f_0}{h} (x - x_0) + + \frac{\Delta^2 f_0}{2!h^2} (x - x_0)(x - x_1) + + \frac{\Delta^3 f_0}{3!h^3} (x - x_0)(x - x_1)(x - x_2) + \text{...} + \frac{\Delta^n f_0}{n!h^n} (x - x_0)(x - x_1) \text{...} (x - x_{n-1})Observe que en la medida que se toman más puntos de muestra, el grado del polinomio puede ser mayor.
[ Dif_Finitas ] || [ Dif_Finitas avanzadas ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] || [ Dif_Divididas_Newton ]
..
2. Ejercicio
Se toman los datos del ejercicio de diferencias finitas , observando que se requiere que el tamaño de paso h sea constante entre los puntos consecutivos xi.
xi = [0.1, 0.2, 0.3, 0.4] fi = [1.45, 1.6, 1.7, 2.0]
Para éste ejercicio se comprueba que h = 0.1
[ Dif_Finitas ] || [ Dif_Finitas avanzadas ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] || [ Dif_Divididas_Newton ]
3. Desarrollo analítico
Se usan los resultados previos del ejercicio con diferencias finitas:
Tabla Diferencia Finita: [['i', 'xi', 'fi', 'df1', 'df2', 'df3', 'df4']] [[ 0. 0.1 1.45 0.15 -0.05 0.25 0. ] [ 1. 0.2 1.6 0.1 0.2 0. 0. ] [ 2. 0.3 1.7 0.3 0. 0. 0. ] [ 3. 0.4 2. 0. 0. 0. 0. ]]
Valores con los que se inicia el cálculo de la distancia entre puntos xi, que debe ser constante:
h = xi[1] – xi[0] = 0.2-0.1 = 0.1
h = xi[2] – xi[1] = 0.3-0.2 = 0.1
h = xi[3] – xi[2] = 0.4-0.3 = 0.1
Para la construcción del polinomio, se usan los valores de diferencias finitas de la primera fila desde la columna 3 en adelante.
dfinita = tabla[0,3:] = [0.15, -0.05, 0.25, 0.]
Se empieza con el valor del primer punto de la función f(0.1)
p3(x) = f0 = 1.45
para añadirle el primer término j=1, más el factor por calcular:
completando el término como:
término = factor(x-x_0) = 1.5(x-0.1) p_3(x) = 1.45 + 1.5(x-0.1)Para el segundo término j=2, se repite el proceso:
factor = \frac{\Delta^2 f_0}{2!h^2} = \frac{-0.05}{2!(0.1)^2} = -2.5 término = factor(x-x_0) = -2.5(x-0.1)(x-02) p_3(x)= 1.45 + 1.5(x-0.1) +(-2.5)(x-0.1)(x-02)Finalmente, añadiendo el tercer término j=3 cuyo cálculo es semejante a los anteriores, se deja como tarea.
El resultado del método es:
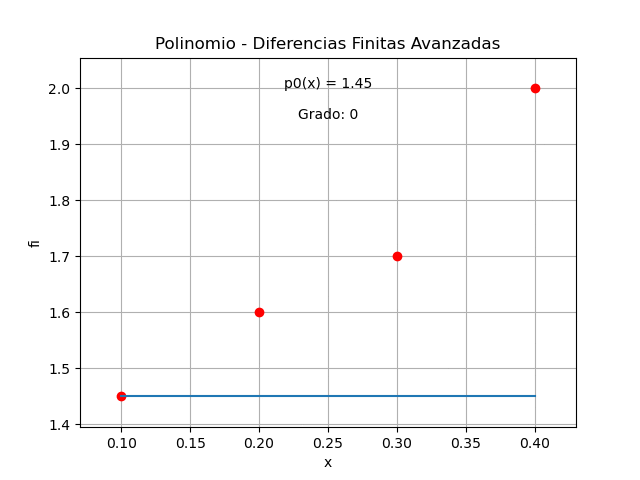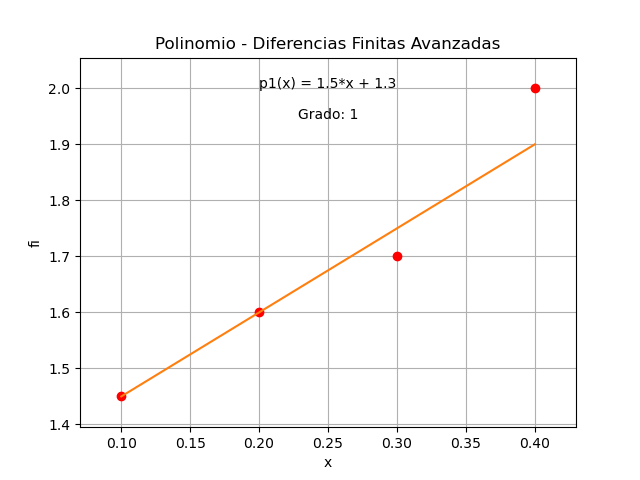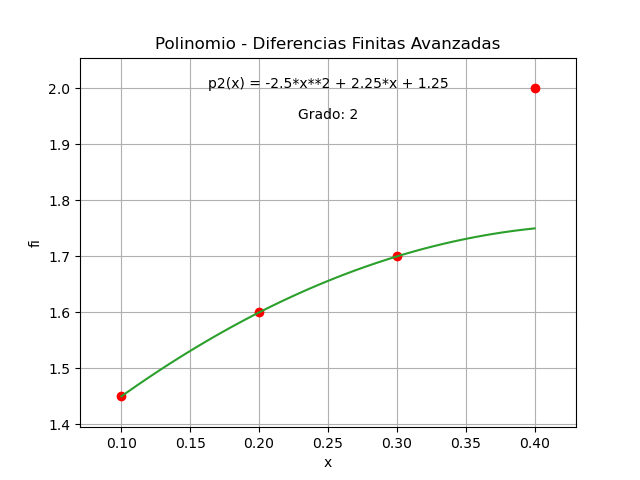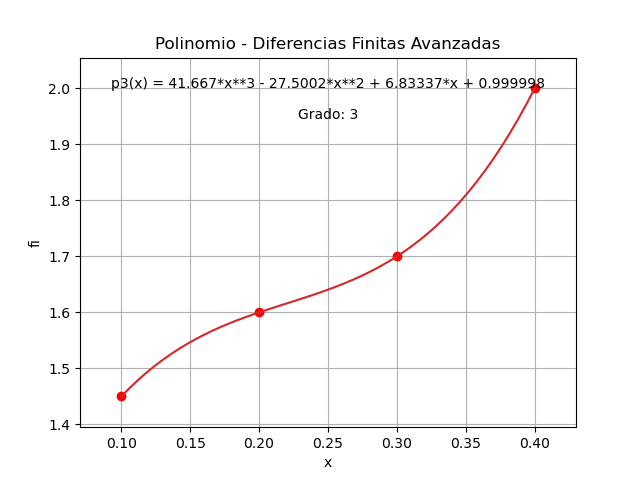
p_3(x)= 1.45 + 1.5(x-0.1) -2.5(x-0.1)(x-02) + + 41.667(x - 0.3)(x - 0.2)(x - 0.1)Se puede seguir simplificando la respuesta, por ejemplo usando solo el término de grado con 1.5(x-0.1) se tiene que:
p_3(x) = 1.3 + 1.5x -2.5(x-0.1)(x-02)+ + 41.667(x - 0.3)(x - 0.2)(x - 0.1)Seguir simplificando la expresión en papel, se deja como tarea.
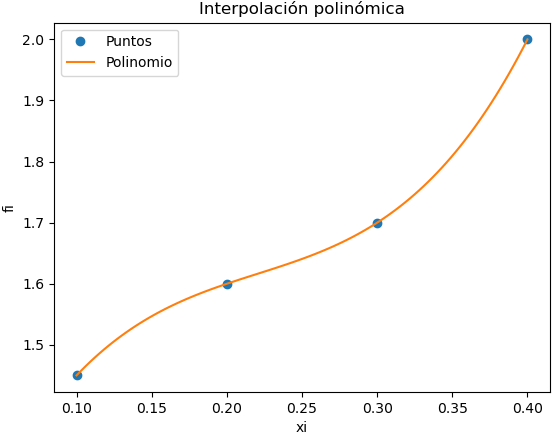
La gráfica del polinomio obtenido comprueba que pasa por cada uno de los puntos dados para el ejercicio.
[ Dif_Finitas ] || [ Dif_Finitas avanzadas ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] || [ Dif_Divididas_Newton ]
..
4. Algoritmo en Python
El polinomio se construye usando el ejercicio de diferencias finitas.
Para construir la expresión del polinomio añadiendo los términos de la fórmula, se define la variable simbólica x con Sympy.
Para simplificar el polinomio resultante con las expresiones de multiplicación, se utiliza la instrucción sym.expand().
En caso de requerir evaluar la fórmula con un vector de datos se la convierte a la forma lambda.
Se añaden las instrucciones para realizar la gráfica en el intervalo [a,b] dado por los valores xi, definiendo el número de muestras = 101 que son suficientes para que la gráfica se observe sin distorsión.
# Polinomio interpolación # Diferencias finitas avanzadas # Tarea: Verificar tamaño de vectores, # verificar puntos equidistantes en x import numpy as np import sympy as sym import matplotlib.pyplot as plt # INGRESO , Datos de prueba xi = [0.1, 0.2, 0.3, 0.4] fi = [1.45, 1.6, 1.7, 2.0] # PROCEDIMIENTO xi = np.array(xi,dtype=float) fi = np.array(xi,dtype=float) # Tabla de Diferencias Finitas titulo = ['i','xi','fi'] n = len(xi) ki = np.arange(0,n,1) tabla = np.concatenate(([ki],[xi],[fi]),axis=0) tabla = np.transpose(tabla) # diferencias finitas vacia dfinita = np.zeros(shape=(n,n),dtype=float) tabla = np.concatenate((tabla,dfinita), axis=1) # Calcula tabla, inicia en columna 3 [n,m] = np.shape(tabla) diagonal = n-1 j = 3 while (j < m): # Añade título para cada columna titulo.append('df'+str(j-2)) # cada fila de columna i = 0 while (i < diagonal): tabla[i,j] = tabla[i+1,j-1]-tabla[i,j-1] i = i+1 diagonal = diagonal - 1 j = j+1 # POLINOMIO con diferencias Finitas avanzadas # caso: puntos equidistantes en eje x h = xi[1] - xi[0] dfinita = tabla[0,3:] n = len(dfinita) # expresión del polinomio con Sympy x = sym.Symbol('x') polinomio = fi[0] for j in range(1,n,1): denominador = np.math.factorial(j)*(h**j) factor = dfinita[j-1]/denominador termino = 1 for k in range(0,j,1): termino = termino*(x-xi[k]) polinomio = polinomio + termino*factor # simplifica multiplicando entre (x-xi) polisimple = polinomio.expand() # polinomio para evaluacion numérica px = sym.lambdify(x,polisimple) # Puntos para la gráfica muestras = 101 a = np.min(xi) b = np.max(xi) pxi = np.linspace(a,b,muestras) pfi = px(pxi) # SALIDA print('Tabla Diferencia Finita') print([titulo]) print(tabla) print('dfinita: ') print(dfinita) print('polinomio: ') print(polinomio) print('polinomio simplificado: ' ) print(polisimple) # Gráfica plt.plot(xi,fi,'o', label = 'Puntos') ##for i in range(0,n,1): ## plt.axvline(xi[i],ls='--', color='yellow') plt.plot(pxi,pfi, label = 'Polinomio') plt.legend() plt.xlabel('xi') plt.ylabel('fi') plt.title('Interpolación polinómica') plt.show()
teniendo como resultado:
Tabla Diferencia Finita [['i', 'xi', 'fi', 'df1', 'df2', 'df3', 'df4']] [[ 0. 0.1 1.45 0.15 -0.05 0.25 0. ] [ 1. 0.2 1.6 0.1 0.2 0. 0. ] [ 2. 0.3 1.7 0.3 0. 0. 0. ] [ 3. 0.4 2. 0. 0. 0. 0. ]] dfinita: [ 0.15 -0.05 0.25 0. ] polinomio: 1.5*x + 41.6666666666667*(x - 0.3)*(x - 0.2)*(x - 0.1) - 2.50000000000001*(x - 0.2)*(x - 0.1) + 1.3 polinomio simplificado: 41.6666666666667*x**3 - 27.5*x**2 + 6.83333333333335*x + 0.999999999999999
el polinomio de puede evaluar como px(valor) una vez que se convierte a la forma lambda para usar con Numpy:
>>> px(0.1) 1.4500000000000004 >>> px(0.2) 1.6000000000000025 >>> px0.3) 1.7000000000000042 >>>
Tarea: se recomienda realizar las gráficas comparativas entre métodos, debe mostrar la diferencia con los métodos que requieren el tamaño de paso equidistante h, y los que no lo requieren. Permite detectar errores de selección de método para interpolación.
[ Dif_Finitas ] || [ Dif_Finitas avanzadas ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] || [ Dif_Divididas_Newton ]