Publicado en por Edison Del Rosario

s2Eva_2022PAOII_T2 EDO – población de protestantes en una sociedad

Ejercicio: 2Eva_2022PAOII_T2 EDO – población de protestantes en una sociedad

\frac{\delta}{\delta t}x(t) = b x(t) - d (x(t))^2 \frac{\delta}{\delta t}y(t) = b y(t) - d (y(t))^2 +r b (x(t)-y(t))

literal a

simplificando la nomenclatura

x' = b x - d x^2 y' = b y - d y^2 +r b (x-y)

sustituyendo constantes, y considerando x(0)=1 ; y(0)=0.01 ; h=0.5

x' = 0.02 x - 0.015 x^2 y' = 0.02 y - 0.015 y^2 +0.1(0.02) (x-y)

el planteamiento de Runge Kutta se hace junto a la primera iteración, además de encontrarse en las instrucciones con Python.

literal b

Se describen 3 iteraciones usando los resultados de la tabla con el algoritmo, para mostrar la comprensión del algoritmo.

t = 0
K1x = 0.5 (0.02 (1) – 0.015 (1)2 = 0.0025
K1y = 0.5(0.02 (0.01) – 0.015 (0.01)2 +0.1(0.02) (1-0.01)= 0.001089

K2x = 0.5 (0.02 (1+0.0025) – 0.015 (1+0.0025)2= 0.00248
K2y = 0.5(0.02 (0.01+0.00108) – 0.015 (0.01+0.00108)2+0.1(0.02) ((1+0.0025)-(0.01+0.00108)) = 0.001101

x1 = 1 + (1/2)(0.0025+0.00248) = 1.0025
y1 = 0.01 + (1/2)(0.001089+0.001101) = 0.01109
t1 = 0 + 0.5 =0.5

t=0.5
K1x = 0.5 (0.02 (1.0025) – 0.015 (1.0025)2 = 0.002487
K1y = 0.5(0.02 (0.01109) – 0.015 (0.01109)2 +0.1(0.02) (1.0025-0.01109)= 0.001101

K2x = 0.5 (0.02 (1.0025+ 0.002487) – 0.015 (1.0025+ 0.002487)2= 0.002474
K2y = 0.5(0.02 (0.01109+0.001101) – 0.015 (0.01109+0.001101)2+0.1(0.02) ((1.0025+ 0.002487)-(0.01109+0.001101)) = 0.001113

x2 = 1.0025 + (1/2)(0.002487+0.002474) = 1.0050
y2 = 0.01109 + (1/2)(0.001101+0.001113) = 0.01220
t2 = 0.5 + 0.5 = 1

t=1
K1x = 0.5 (0.02 (1.0050) – 0.015 (1.0050)2 = 0.002474
K1y = 0.5(0.02 (0.01220) – 0.015 (0.01220)2 +0.1(0.02) (1.0050-0.01220)= 0.001113

K2x = 0.5 (0.02 (1.0050+ 0.002474) – 0.015 (1.0050+ 0.002474)2= 0.002462
K2y = 0.5(0.02 (0.01220+0.001113) – 0.015 (0.01220+0.001113)2+0.1(0.02) ((1.0050+ 0.002474)-(0.01220+0.001113)) = 0.001126

x3 = 1.0050 + (1/2)(0.002474+0.002462) = 1.0074
y3 = 0.01220 + (1/2)(0.001113+0.001126) = 0.01332
t3 = 1 + 0.5 = 1.5

Resultado con el algoritmo

Para obtener los datos de las iteraciones, primero se ejecuta el algoritmo para pocas iteraciones.
Para la pregunta sobre 200 años, se incrementa las iteraciones a 2 por año y las condiciones iniciales, es decir 401 muestras.

 [ ti, xi, yi]
 [ ti, xi, yi]
[[0.0000e+00 1.0000e+00 1.0000e-02 0.0000e+00 0.0000e+00 0.0000e+00 0.0000e+00]
 [5.0000e-01 1.0025e+00 1.1095e-02 2.5000e-03 1.0892e-03 2.4875e-03 1.1014e-03]
 [1.0000e+00 1.0050e+00 1.2203e-02 2.4875e-03 1.1014e-03 2.4749e-03 1.1136e-03]
 [1.5000e+00 1.0074e+00 1.3323e-02 2.4749e-03 1.1137e-03 2.4623e-03 1.1260e-03]
 [2.0000e+00 1.0099e+00 1.4455e-02 2.4624e-03 1.1260e-03 2.4497e-03 1.1384e-03]
 [2.5000e+00 1.0123e+00 1.5600e-02 2.4498e-03 1.1384e-03 2.4371e-03 1.1509e-03]
 [3.0000e+00 1.0148e+00 1.6757e-02 2.4371e-03 1.1509e-03 2.4245e-03 1.1634e-03]
 [3.5000e+00 1.0172e+00 1.7926e-02 2.4245e-03 1.1635e-03 2.4118e-03 1.1761e-03]
 [4.0000e+00 1.0196e+00 1.9109e-02 2.4118e-03 1.1761e-03 2.3991e-03 1.1888e-03]
...
 [1.9950e+02 1.3252e+00 1.1561e+00 ... 1.7202e-03 8.1217e-05 1.7059e-03]
 [2.0000e+02 1.3252e+00 1.1578e+00 ... 1.7060e-03 8.0418e-05 1.6918e-03]
 [2.0050e+02 1.3253e+00 1.1595e+00 ... 1.6919e-03 7.9628e-05 1.6778e-03]]
>>>

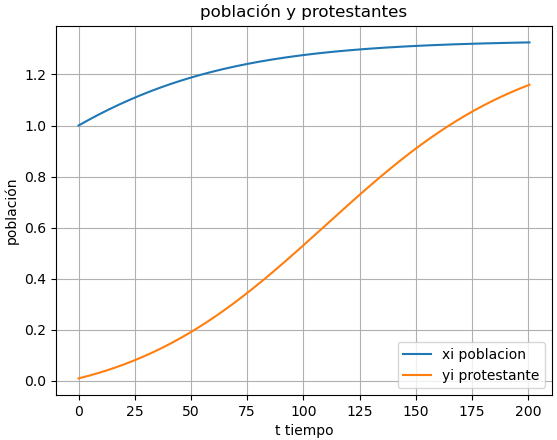
Observación: La población identificada como protestante, continua creciendo, mientras que la proporción de «conformistas» se reduce según los parámetros indicados en el ejercicio. Los valores de natalidad y defunción cambian con el tiempo mucho más en años por otras variables, por lo que se deben realizar ajustes si se pretende extender el modelo.

2Eva2022PAOII_T2 poblacion protestantes
Instrucciones en Python

# Modelo predador-presa de Lotka-Volterra
# Sistemas EDO con Runge Kutta de 2do Orden
import numpy as np

def rungekutta2_fg(f,g,t0,x0,y0,h,muestras):
    tamano = muestras +1
    tabla = np.zeros(shape=(tamano,7),dtype=float)
    tabla[0] = [t0,x0,y0,0,0,0,0]
    ti = t0
    xi = x0
    yi = y0
    for i in range(1,tamano,1):
        K1x = h * f(ti,xi,yi)
        K1y = h * g(ti,xi,yi)
        
        K2x = h * f(ti+h, xi + K1x, yi+K1y)
        K2y = h * g(ti+h, xi + K1x, yi+K1y)

        xi = xi + (1/2)*(K1x+K2x)
        yi = yi + (1/2)*(K1y+K2y)
        ti = ti + h
        
        tabla[i] = [ti,xi,yi,K1x,K1y,K2x,K2y]
    tabla = np.array(tabla)
    return(tabla)

# PROGRAMA ------------------

# INGRESO
# Parámetros de las ecuaciones
b = 0.02
d = 0.015
r = 0.1

# Ecuaciones
f = lambda t,x,y : (b-d*x)*x
g = lambda t,x,y : (b-d*y)*y + r*b*(x-y)

# Condiciones iniciales
t0 = 0
x0 = 1
y0 = 0.01

# parámetros del algoritmo
h = 0.5
muestras = 401

# PROCEDIMIENTO
tabla = rungekutta2_fg(f,g,t0,x0,y0,h,muestras)
ti = tabla[:,0]
xi = tabla[:,1]
yi = tabla[:,2]

# SALIDA
np.set_printoptions(precision=6)
print(' [ ti, xi, yi, K1x, K1y, K2x, K2y]')
print(tabla)

# Grafica tiempos vs población
import matplotlib.pyplot as plt

plt.plot(ti,xi, label='xi poblacion')
plt.plot(ti,yi, label='yi protestante')

plt.title('población y protestantes')
plt.xlabel('t años')
plt.ylabel('población')
plt.legend()
plt.grid()
plt.show()

# gráfica xi vs yi
plt.plot(xi,yi)

plt.title('población y protestantes [xi,yi]')
plt.xlabel('x población')
plt.ylabel('y protestantes')
plt.grid()
plt.show()