s2Eva_2023PAOII_T2 Cable cuelga entre apoyos A y B

Ejercicio: 2Eva_2023PAOII_T2 Cable cuelga entre apoyos A y B

Literal a

La ecuación diferencial a resolver es:

\frac{d^2y}{dx^2} = \frac{w_0}{T_0} \Big[ 1+ \sin \Big(\frac{\pi x}{2l_B} \Big) \Big]

donde w₀ = 1 000 lbs/ft, T₀. = 0.588345×10⁶.
dy(0)/dx = 0 y l_B=200 de la gráfica presentada.

\frac{d^2y}{dx^2} = \frac{1000}{0.588345×10^6} \Big[ 1+ \sin \Big(\frac{\pi x}{2(200)} \Big) \Big]

Para usar Runge Kutta para segunda derivada:

z= y' = f(x,y,z) z' = (y')' = 0z + \frac{1000}{0.588345×10^6} \Big[ 1+ \sin \Big(\frac{\pi x}{2(200)} \Big) \Big] g(x,y,z) = \frac{1}{0.588345×10^3} \Big[ 1+ \sin \Big(\frac{\pi x}{2(200)} \Big) \Big]

los valores iniciales para el ejercicio acorde al enunciado son: x₀ = 0, y₀=0, z₀ = 0, con h=0.5

literal b

para itera 0

K1y = h*z = 0.5*0 = 0 K1z = (0.5)\frac{1}{0.588345×10^3} \Big[ 1+ \sin \Big(\frac{\pi (0)}{2(200)} \Big) \Big] = 0.0008498 K2y = h*(z+K1z) = (0.5) (0+0.00084984) = 0.0004249 K2z = (0.5)\frac{1}{0.588345×10^3} \Big[ 1+ \sin \Big(\frac{\pi (0+0.5)}{2(200)} \Big) \Big] =0.0008531 y = 0+\frac{0+0.0004249}{2} = 0.0002124 z = 0+\frac{0.0008498+0.0008531}{2} = 0.0008515 x = 0 + 0.5 = 0.5

…

Desarrollar dos iteraciones adicionales como tarea.

Para las primeras iteraciones de un total de 400+1, los valores con Python y en resultados.txt :

estimado[xi,yi,zi,K1y,K2y,K1z,K2z]
[0.0000 0.0000e+00 0.0000e+00 
0.0000e+00 0.0000e+00 
0.0000e+00 0.0000e+00]

[0.5000 2.124603761398499073e-04 8.515101601627471980e-04 
0.000000000000000000e+00 4.249207522796998146e-04 
8.498415045593996292e-04 8.531788157660947667e-04]

[1.0000 8.515101601627470896e-04 1.706357605799455881e-03 
4.257550800813735990e-04 8.523444879644209281e-04 
8.531788157660947667e-04 8.565160755073224913e-04]

[1.5000 1.918817981939305653e-03 2.564542259712321911e-03 
8.531788028997279406e-04 1.281436840653389295e-03 
8.565160755073224913e-04 8.598532323184093513e-04]

[2.0000 3.416052419875068892e-03 3.426063993239661116e-03 
1.282271129856160955e-03 1.712197746015365740e-03 
8.598532323184093513e-04 8.631902347362692754e-04]
...

literal c

resultado en archivo.txt al ejecutar el algoritmo.

literal d

Algoritmo con Python

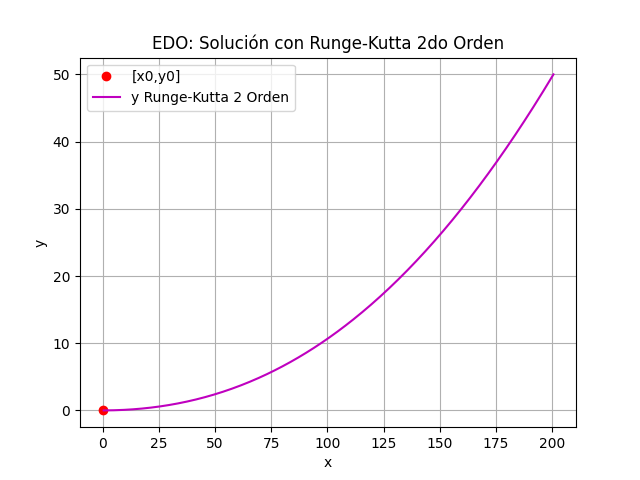
# 2Eva_2023PAOII_T2 Cable cuelga entre apoyos A y B
import numpy as np

def rungekutta2_fg(f,g,x0,y0,z0,h,muestras):
    tamano = muestras + 1
    estimado = np.zeros(shape=(tamano,3+4),dtype=float)

    # incluye el punto [x0,y0,z0]
    estimado[0] = [x0,y0,z0,0,0,0,0]
    xi = x0
    yi = y0
    zi = z0
    for i in range(1,tamano,1):
        K1y = h * f(xi,yi,zi)
        K1z = h * g(xi,yi,zi)
        
        K2y = h * f(xi+h, yi + K1y, zi + K1z)
        K2z = h * g(xi+h, yi + K1y, zi + K1z)

        yi = yi + (K1y+K2y)/2
        zi = zi + (K1z+K2z)/2
        xi = xi + h
        
        estimado[i] = [xi,yi,zi,K1y,K2y,K1z,K2z]
    return(estimado)

# PROGRAMA PRUEBA
# Ref Rodriguez 9.1.1 p335 ejemplo.
# prueba y'-y-x+(x**2)-1 =0, y(0)=1

# INGRESO
T0 = 0.588345e6
LB = 200
f = lambda x,y,z: z
g = lambda x,y,z: (1000/T0)*(1+np.sin(np.pi*x/(2*LB)))
x0 = 0
y0 = 0
z0 = 0
h  = 0.5
muestras = 401

# PROCEDIMIENTO
puntosRK2 = rungekutta2_fg(f,g,x0,y0,z0,h,muestras)
xi = puntosRK2[:,0]
yiRK2 = puntosRK2[:,1]

# SALIDA
np.set_printoptions(precision=4)
print('estimado[xi,yi,zi,K1y,K2y,K1z,K2z]')
print(puntosRK2)
np.savetxt("tablaRk2.txt",puntosRK2)


# Gráfica
import matplotlib.pyplot as plt

plt.plot(xi[0],yiRK2[0],
         'o',color='r', label ='[x0,y0]')
plt.plot(xi[1:],yiRK2[1:],
         color='m',
         label ='y Runge-Kutta 2 Orden')

plt.title('EDO: Solución con Runge-Kutta 2do Orden')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid()
plt.show()